Задачи для самостоятельной работы. Модули О, ОЧП, ОЭ. Линейная алгебра

Модуль К Категория

Вход

Модули О, ОЧП, ОЭ. Линейная алгебра. Анализ

Выход

Понятия

Система

Подсистема Идеальная с.

Элемент с.С. всех множеств, ObS

Множество Элемент м.

ОтношениеУпорядоченная

пара

Отображение Упорядоченная

тройка

Правило

композиции Категория, М. морфизмов, Морфизм Объект С. объектов,

морфизмов, K K(X, Y)к. Кк. К ObK

ComK

S L T M N

Отношение Отношение

подкатегории изоморфности объектов Изоморфизм Обратный морфизм

в к. Кк.Кк. К

Пусть....	Понятие, обозначение	Определяющее понятие и видовые признаки
	Категория (к.), K	Упорядоченная тройка <ObK, K(X, Y) " X,Y Î ObK, ComK>, где ObK- с. объектов к. K, K(X, Y) - м. морфизмов к. Кобъекта X в объект Y, ComK -правило композиции морфизмов в к. K
K- к.	С. объектов к. K, ObK	Идеальная с., элементами которой являются объекты к. K
K- к.	Объект к. K,XÎ ObK	Элемент с. ObK
K- к., X,YÎ ObK	М. морфизмов к. K, K(X, Y)	Множество K(X, Y)всех морфизмов к. Kобъекта X в объект Y
K- к., X,YÎ ObK	Морфизм к. K, A:X®Y	Элемент м. K(X, Y)
K- к., X,Y,Z,WÎ ObK,A:X®Y, B:Y®Z, C:Z®W- морфизмы к. K	Правило композиции морфизмов в к. K, ComK	Отображение K(X, Y) ´ K(Y, Z) ® K(X, Z), обладающее свойствами: 1. Ассоциативность: C*(B*A) = (C*B)*A, 2. Существование единицы: " YÎObK $ 1Y ÎK(Y, Y)½ 1Y *A = A " A Î K(X, Y)& B*1Y = B " B Î K(Y, Z)
K,P- к.	Отношение “Pподкатегория K”	Бинарное отношениево м. всех категорий, которое задается отношениями: 1. ObP Í ObK 2. P(X,Y) Í K(X,Y)" X,Y Î ObP 3. ComP = ComK½P(X,Y) ´ P(Y,Z) (т.е. правила композиции в Kи Pсовпадают)
K- к., A Î K(X,Y)	Обратный морфизм в к. К, A-1	МорфизмA-1 Î K(Y,X)ç A*A-1 = 1Y & A-1 *A= 1X
K- к.	Изоморфизм в к. K	Морфизмк. K, для которого существует обратный морфизм
K- к. X, Y Î ObK	Отношение изоморфности объектов, X ~ Y	Бинарное отношениена ObK: X ~ Y Û $ изоморфизм A:X®Y
	Категория множеств и отображений, S	Категория S, для которой: ObSсостоит из всех м., S(X,Y)состоит из всех о. A:X®Y, ComSопределяется формулами: 1° (B*A)(x) = B[A(x)] 2° 1x(x) = x
	Категория линейных пространств (л.п.) и линейных отображений (л.о.), L	Категория L, для которой: ObLсостоит из всех л.п., L(X,Y)состоит из всех л.о. A:X®Y, ComL = ComS½L(X,Y) ´ L(Y,Z)(т.е. композиции и единицы в Lи Sсовпадают)
	Категория топологических пространств (т.п.) и непрерывных отображений (н.о.), T	Категория T, для которой: ObTсостоит из всех т.п., T(X,Y)состоит из всех н.о. A:X®Y, ComT = ComS½T(X,Y) ´ T(Y,Z)(т.е. композиции и единицы в Tи Sсовпадают)
	Категория метрических пространств (м.п.) и непрерывных отображений (н.о.), M	Категория M, для которой: ObMсостоит из всех м.п., M(X,Y)состоит из всех н.о. A:X®Y, ComM = ComS½M(X,Y) ´ M(Y,Z)(т.е. композиции и единицы в Mи Sсовпадают)
	Категория нормированных пространств (н.п.) и линейных непрерывных отображений (л.н.о.), N	Категория N, для которой: ObNсостоит из всех н.п., N(X,Y)состоит из всех л.н.о. A:X®Y, ComN = ComS½N(X,Y) ´ N(Y,Z)(т.е. композиции и единицы в Nи Sсовпадают)
X Î ObS	Топологическое пространство (т.п.), Х	Упорядоченная пара <X, t>, где t- топология во м. Х
X Î ObS	Топология в Х, t	Подмножество t Í Ã(X) со свойствами: 1° {Æ, X} Í t 2° u, v Î tÞ u Ç v Ît 3° s Í t Þîþu Î t uÎs
X Î ObT	Открытое м. в т.п	Элементтопологии t
X Î ObT, xÎX	Окрестность точки x, ux	Открытое м.ux, содержащее точку х (т.е. xÎ ux Î t)
<X,tX>, <Y, tY> Î ObT	Непрерывное о., AÎ T(X,Y)	ОтображениеA:X®Y со свойством "(x Î X, uAx Î tY ) $ vx Î tX ½ A(vx) Í uAx
X Î ObS	Метрическое пространство (м.п.), Х	Упорядоченная пара <X, d>, где d -метрика во м. Х
X Î ObS	Метрика (в Х)	Функция d : X´X ® [0, +¥) ½ " x,y,z Î X 1° d(x,y) = 0 Û x = y 2° d(x,y)= d(y,x) 3° d(x,y)£d(x,z) + d(z,y)
<X, d> Î ObM, xn , x Î X	Сходящаяся к х последовательность, xn ® x	Последовательностьxn ½ n ® ¥ Þd(xn , x) ® 0
<X, d> Î ObM, xn Î X	Фундаментальная последовательность	Последовательностьxn ½ n,m ® ¥ Þd(xn , xm ) ® 0
X Î ObM	Полное м.п.	М.п., в котором " фундаментальная последовательность сходится (к некоторому x Î X)
<X,dX>, <Y, dY> Î ObM	Непрерывное о. в м.п., A Î M(X,Y)	ОтображениеA:X®Y со свойством: (x Î X, xn ® x) Þ Axn ® Ax
X Î ObM, x Î X, r > 0	Шар (в м.п.), Bx,r	Подмножество Bx,r = {yÎX½ d(x,y) < r} Í X
X - м.п.	Топология окрестностей в м.п. X, tO	Топология tO = {u Î Ã(X)½ x Î u Þ u Ê Bx,r для некоторого r> 0 }
X Î ObL	Нормированное пространство (н.п.), Х	Упорядоченная пара <X,|| . || >, где || . || -норма в л.п. Х
X Î ObL	Норма, || . ||	Функция|| . ||: X ® [0, +¥) ½" x,yÎ X, l Î R(C) 1° || x || = 0 Û x = q 2° || lx || = ½l½ || x || 3° || x + y || £ || x || + || y ||
<X,|| . || > Î ObN	Банахово пространство (б.п.)	Полное н.п.относительно метрики d(x,y) = || x - y ||
<X,||.||X>, <Y,||.||Y>ÎObN	Непрерывное л.о. в н.п., A Î N(X,Y)	ОтображениеA:X®Y с 2 свойствоми: 1° А непрерывно; 2° А линейно
	Гомеоморфизм	Изоморфизмв категории T
P Î ObS; PR - м. высказываний; A,B Î S(P, PR)	Демон системы знаний, A(p) =(di =<имя демона>)Þ B(p), AÞB	НеравенствоA £ B в ЧУМ S(P,PR)
AÞB и BÞA - демоны СЗ	Двойной демон СЗ, A(p) Ü(di = <имя демона> )Þ B(p), АÛB	Объединениедемонов СЗ (AÞB)È(BÞA) = АÛB

Утверждения

УТВ К-1 ОЧП категорийОтношение подкатегории является ОЧП на м. всех категорий, причем, если знак неравенства £ заменить стрелкой ® , то имеет место следующаяя семантическая сеть (дуги, вытекающие из транзитивности ОЧП, не указаны):

S

T

L N M

УТВ К - 2 Об изоморфизмах

2.1Отношение изоморфности является отношением эквивалентности в ObK

2.2Изоморфизмы в к. S, L, N. Пусть A Î S(X,Y)(L(X,Y), N(X - б.п.,Y- б.п.)). Тогда:

A - изоморфизм в к. S ( в к. L,в к.N) ÛA - биекция

УТВ К - 3 Примеры объектов и морфизмов

3.1Объекты и морфизмы к. S

1° X, Y Î ObSÞ S(X,Y)Î ObS

2° A Î S(X,Y)Þ A Î ObS

3° Все рассмотреные выше м., в частности, все ф.п. являются, очевидно, объектами к. S, а все отображения, в частности, все функции, функционалы, операторы являются, очевидно, морфизмами к. S

3.2Объекты и морфизмы к. L

1° X Î ObS,Y Î ObLÞ S(X,Y)Î ObL, причем алгебраические операции вводятся в S(X,Y)поточечно.

2° X, Y Î ObLÞ L(X,Y)Î ObL,причем алгебраические операции вводятся в L(X,Y)поточечно.

3° X, Y Î ObLÞ X ´ Y Î ObL, причем алгебраические операции вводятся в X ´ Y покомпонентно.

4° A Î L(X,Y)Þ A Î ObL

5° Все рассмотреные выше ф.п. C[a, b], l_p, ...являются объектами к. L, а рассмотренные функционалы (интегральный и d-функция) и операторы (умножения на фиксированную функцию, интегральный, дифференциальный) являются морфизмами к. L

3.3Объекты и морфизмы к. N

1° X, Y Î ObNÞ N(X,Y)Î ObN

2° A Î N(X,Y)Þ A Î ObN

3°Две наиболее распространенные нормы функций x: T ® R(x: T ® C):

sup-норма || x ||_sup = sup{½x(t)½: t Î T}

интегральная p-норма (p ³ 1) T = [a, b] Þ || x ||_p =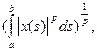

T = NÞ || x ||_p =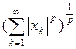

4° Все рассмотреные выше ф.п. C[a, b], l_p, ...являются объектами к. N:

<C[a, b],|| . ||_sup >, <l_p, || . ||_p >, <L_p [a, b], || . ||_p >,

<C^k[a, b],|| x || =|| x^(k) ||_sup +|| x ^{(k - 1)} ||_sup + ... +|| x ||_sup >,

а рассмотренные функционалы и операторы являются морфизмами к. N

3.4Объекты и морфизмы к. MиT

1° N £ M £ T =( по определению отношения подкатегории)Þ ObN Í ObM Í ObT& N(X,Y) Í M(X,Y) Í T(X,Y)" X,Y Î ObN(т.е. примеры объектов и морфизмов категории Nявляются в то же время примерами объектов и морфизмов категорий Mи T).

Умения

УМ К-1 Доказать истинность данного утверждения:

1° Представить утверждение в видедемона СЗ AÞB (двойного демона СЗ AÛB, нескольких демонов СЗ)(т.е. определить, что дано и что требуется доказать?)

2° Выделить параметрические высказывания A, B Î S(P,PR), входящие в демон СЗ AÞ B (двойной демон СЗ АÛВ) и определить м. параметров Р;

3° Определить категорию (категории), в которой (предположительно) определяются исползуемые в доказательстве известные ранее демоны СЗ;

4° Построить цепочку известных (истинных) демонов СЗ (двойных демонов СЗ):

A(p) =( d₁)Þ A₁(p) =( d₂)Þ A₂(p) =( d₃)Þ A₃(p) Þ ... ÞA_n-1(p) =( d_n)Þ B(p)

(A(p) Ü( d₁)Þ A₁(p) Ü( d₂)Þ A₂(p) Ü( d₃)Þ A₃(p) Û ... ÛA_n-1(p) Ü( d_n)Þ B(p)),

“соединяющих” параметрические высказывания А и В и, следовательно, в силу транзитивности ОЧП, доказывающих истинность данного исходного демона СЗ.

Примеры

ПР К-1 Доказать утверждение об изоморфизме в к. L(утв К2.2). Пусть A Î L(X,Y).Тогда:

A - изоморфизм в L ÛA - биекция.

1° A - изоморфизм в к. L Û A - биекция- двойной демон СЗ, истинность которого необходимо доказать (параметр A Î L(X,Y)).

2° A(p)= “A - изоморфизм в к. L”, B(p)= “А - биекция”, P = L(X,Y)' p= A.

3° Очевидно, что будут использоваться категории Lи S(биекция - понятие из к. S).

4° ¨А - изоморфизм в LÜ( d₁ = “определение изоморфизма”)Þ $ A^-1 Î L(Y,X)½ A A^-1 = 1_y & A^-1 A= 1_x =( d₂ = “L £ S” )Þ Ú Ü( d₃ = "о., обратное линейному, линейно" - ? )=
A Î L(X,Y)Í S(X,Y)& $ A^-1 Î S(Y,X)½ A A^-1 = 1_y & A^-1 A= 1_x Ü( d₄ = “определение обратимого о.”)Þ A обратим Ü( d₅ = “критерий обратимости о. в к. S”)Þ А - биекция ¨

Осталось установить истинность демона d₃ = “о., обратное линейному, линейно” =

A Î L(X,Y)Í S(X,Y)& $ A^-1 Î S(Y,X) ÞA^-1 Î L(Y,X)

Проверим истинность этого демона, используя демон “определение л.о.” (нумерацию демонов можно опускать, т.к. все они, как правило, имеют уникальные имена):

¨í y₁, y₂ Î Y & l₁, l₂ Î R(C) Þ A^-1 (l₁ y₁ + l₂ y₂) =( $ A^-1 Þ y₁ = Ax₁ & y₂ = Ax₂ )=
A^-1 (l₁ Ax₁ + l₂ Ax₂) =( A Î L(X,Y))Þ A^-1 [A(l₁ x₁ + l₂ x₂)] =( определение композиции A^-1 A)= A^-1 A(l₁ x₁ + l₂ x₂) =( A^-1 A= 1_x и определение 1_x )= l₁ x₁ + l₂ x₂ =
=( x₁ = A^-1 y₁ & x₂ = A^-1 y₂)= l₁ A^-1 y₁ + l₂ A^-1 y₂ ý Ü( определение л.о.)Þ A^-1 Î L(Y,X) ¨

Доказательство можно теперь окончательно оформить.

Утверждение Пусть A Î L(X,Y).Тогда:

A - изоморфизм в L ÛA - биекция.

Доказательство¨А - изоморфизм в LÜ(определение изоморфизма)Þ $ A^-1 Î L(Y,X)½ A A^-1 = 1_y & A^-1 A= 1_x =(L £ S)Þ Ú Ü( ? -см. лемма ниже)= A Î L(X,Y)Í S(X,Y)&
$ A^-1 Î S(Y,X)½ A A^-1 = 1_y & A^-1 A= 1_x Ü(определение обратимого о.)Þ A обратим Ü(критерий обратимости о. в к. S)Þ А - биекция ¨

Лемма Пусть A Î L(X,Y).Тогда:

A Î L(X,Y)Í S(X,Y)& $ A^-1 Î S(Y,X) ÞA^-1 Î L(Y,X)

(О., обратное линейному, линейно)

Доказательство леммы

¨í y₁, y₂ Î Y & l₁, l₂ Î R(C) Þ A^-1 (l₁ y₁ + l₂ y₂) =( $ A^-1 Þ y₁ = Ax₁ & y₂ = Ax₂ )=
A^-1 (l₁ Ax₁ + l₂ Ax₂) =( A Î L(X,Y))Þ A^-1 [A(l₁ x₁ + l₂ x₂)] =( определение композиции A^-1 A)= A^-1 A(l₁ x₁ + l₂ x₂) =( A^-1 A= 1_x и определение 1_x )= l₁ x₁ + l₂ x₂ =
=( x₁ = A^-1 y₁ & x₂ = A^-1 y₂)= l₁ A^-1 y₁ + l₂ A^-1 y₂ ý Ü( определение л.о.)Þ A^-1 Î L(Y,X) ¨

Задачи для самостоятельной работы

1. Доказать, что данное о. является морфизмом категории N.

Варианты

1. Fx = x(0) (d-функция Дирака).

2. Пусть а:[0,1]®R –непрерывная функция. Оператор умножения (на а)

(Ax)(t) = a(t)x(t).

3. Пусть k:[0,1]®R –непрерывная функция. Интегральный функционал

Fx =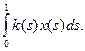

4. Пусть k:[a,b]´[c,d]®R –непрерывная функция. Интегральный оператор

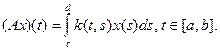
5. Пусть g:[0,1]®[0,1] - непрерывная функция. Оператор внутренней суперпозиции

(Ax)(t) = x[g(t)].

Указание. Доказывать по схеме:

1. Выбрать X,YÎObS. Доказать AÎS(X,Y).

2. Доказать, что X,YÎObL. Доказать AÎL(X,Y).

3. Доказать, что X,YÎObM. Доказать AÎM(X,Y).

4. Доказать, что X,YÎObN. Доказать AÎN(X,Y).

2. Доказать.

Варианты

1. Отношение изоморфности является отношением эквивалентности в ObK

2. A Î S(X,Y)Þ A Î ObS.

3. L – категория.

4. X Î ObS,Y Î ObLÞ S(X,Y)Î ObL.

5. <C^k[a, b],|| . || > ÎObN.

6. X, Y Î ObLÞ L(X,Y)Î ObL.

7. M– категория.

8. < B[a,b], || . ||_sup > ÎObN.

9. < C[a,b], || . ||_sup > ÎObN.

10. T – категория.

11. ObM Í ObT.

12. < l₁, || . ||₁ > ÎObN.

13. X, Y Î ObLÞ X ´ Y Î ObL.

14. A Î L(X,Y)Þ A Î ObL.

15. N £ M.

16. N £ L.

17. X,YÎObM Þ M(X,Y) Í T(X,Y).

18. < L₁[a,b], || . ||₁ > ÎObN.

19. I – категория.

Образец решения (1 задание).

Доказать, что оператор (Ax)(t) = x(1) ´ sin t является морфизмом категории N, т.е. AÎN(X,Y) для некоторых нормированных пространств X и Y.

1. Выберем X = Y = C[0,1] = {x:[0,1]®R | x непрерывна} – множество всех непрерывных на отрезке [0,1] функций =(определение ObS)Þ XÎObS!

AÎS(X,X) = S(X)?

Д-во. xÎC[0,1] =(const´sint:[0,1]®R непрерывна)Þ AxÎC[0,1] =(определение S(C[0,1]))Þ AÎS(X)!

2. XÎObL? Введем поточечные алгебраические операции в C[0,1]:

"(l,mÎR; x,yÎX; tÎ[0,1]) (lx + my)(t) =(поточечные алгебраические операции)= lx(t) +_R my(t). В частности,
q(t) = 0 "tÎ[0,1]. Докажем, что складывая и умножая на числа векторы из X, мы получаем снова векторы из Х?

Д-во. "(l,mÎR;x,yÎX) =(теорема из анализа: линейная комбинация непрерывных функций непрерывна)Þ
lx + myÎX =(определение линейного пространства ?)Þ X = C[0,1] – л.п. =(определение ObL)Þ XÎObL!

AÎL(X)?

Д-во. "t A(lx + my)(t) =(определение о. А)= (lx + my)(1) sin t =(поточечные алгебраические операции)= [lx(1) +_R my(1)] sin t =(R– л.п.)= lx(1) sin t +_R my(1) sin t =(определение о. А)= l(Ax)(t) +_R m(Ay)(t) =(поточечные алгебраические операции)= (lAx + mAy)(t) Ü(поточечное равенство функций)Þ
A(lx + my) = lAx + mAy Ü(определение л.о.)Þ А – л.о. Ü(определение L(X))Þ AÎL(X)!

3. XÎObM? Т.к. ObN Ì ObM (d(x,y) = ||x - y|| ?), сразу введем в л.п. X = C[0,1] норму

xÎ C[0,1] ® ||x||_sup = sup{|x(t)| : tÎ[0,1]} (= sup |x| ([0,1]) = sup im |x| ).

Докажем, что функция x ® ||x||_sup удовлетворяет аксиомам нормы.

||x ||_sup : X ® [0, +¥) ?

Д-во.xÎ C[0,1] = X =(теорема Вейерштрасса: непрерывная на отрезке функция x:[0,1]®R ограничена)Þ
0 £ |x(t)| £ M < ¥ "tÎ[0,1], т.е. М – мажоранта для im |x| =(sup наименьшая мажоранта)Þ 0 £ ||x||_sup £ M < ¥ ,
т.е. ||x||_sup Î [0, +¥) !

Невырожденность || · ||_sup?

Д-во. ?

||lx ||_sup = |l| ||x ||_sup ?

Д-во.||lx||_sup =(определение sup-нормы)= sup{|lx(t)| : tÎ[0,1]} =(|lm| = |l||m|)= sup{|l||x(t)| : tÎ[0,1]}
=(suplW = lsupW " (l³0, WÍ[0,+¥))= |l| ||x||_sup – полуднородность sup-нормы доказана !

Неравенство треугольника ?

Д-во. "t |(x + y)(t)| =(поточечные алгебраические операции)= |x(t) + y(t)| £(неравенство D для чисел)£
|x(t)| + |y(t)| £(sup-норма – мажоранта)£ ||x||_sup + ||y||_sup =( sup-норма – наименьшая мажоранта)Þ
||x + y||_sup £ ||x||_sup + ||y||_sup ! =(определение нормированного пространства)Þ упорядоченная пара
<C[0,1], ||·||_sup> =(обозначение)= C[0,1] = X - нормированное пространство Ü(определение ObN)Þ
XÎObN =( ObN Ì ObM )Þ XÎObM !

A Î N(X) Ì M(X)? A – л.о. – доказано выше. Осталось доказать, что А – непрерывное отображение ?

Д-во. x_n ® x Ü(определение сходимости в Х)Þ d(x_n, x) = ||x_n - x||_sup ® 0 при n®¥ ( * ). "t |(Ax_n– Ax)(t)|=(поточечные алгебраические операции)= |(Ax_n)(t) – (Ax)(t)| =(определение о.А)= | x_n(1) ´ sin t - x(1) ´ sin t|
=(R – поле)= | (x_n(1) - x(1))| |sin t| =(поточечные алгебраические операции)= | (x_n– x)(1)| |sin t| £(определение sup-нормы)£ ||x_n - x||_sup ||sin||_sup =( sup-норма – наименьшая мажоранта)Þ 0 £ ||Ax_n - Ax||_sup £ ||x_n - x||_sup ||sin||_sup ® 0 при n®¥ - см. (*) и sin Î C[0,1] =(лемма о двух милиционерах)Þ ||Ax_n - Ax||_sup ® 0 при n®¥ Ü(определение сходимости в н.п. Х)Þ Ax_n ® AxÜ(определение непрерывного отображения в нормированных пространствах)Þ А – н.о.! Следовательно, т.к. А - л.о. и А – н.о., то, по определению N(X), AÎ N(X) =(N(X)ÍМ(X))Þ AÎ М(X)!

4. Выше уже доказано, что C[0,1] = XÎObN, а оператор AÎ N(X) §

3. Решите "свой" вариант теста (не забудьте указать вариант, например, ТЕСТ К - 1). Тестовое задание (ТЗ) с номером № студента (mod12) представьте с решением, на остальные ТЗ пришлите только ответы.

Варианты

1. ТЕСТ К - 1.

№	А	В	Дополнительная информация
	Открытое м.ux, содержащее точку х (т.е. xÎ ux Î t)	Подмножество в X	Понятия
	Нормированное пространство (н.п.)	Л.п. с нормой	Понятия
	А изоморфизм в L	$ A-1 Î L(Y,X)	Пар. выс-я AÎL(X,Y)
	$ A-1 Î M(Y,X)	А изоморфизм в M	Пар. выс-я AÎM(X,Y)
	Категория л.п. и л.н.о.	Категория т.п. и н.о.	Категории
	Категория м. и о.	Мн-во морфизмов кат. м. и о.	Категории
	xn ® x	Axn ® Ax	П.в-я.AÎN(X,Y)
	X ~ Y в M	$ обратимый AÎM(X,Y)	П.в. X,YÎObM
	AÎObS	AÎS(X,Y)	П.в. AÎObS
	Aa Î L(C[0,1])	Aa Î N(C[0,1])	П.в. aÎC[0,1]
	||x||sup	||x||2	Числа x(t) = t, x:[0,1]®R
	UÈV Î tX	U,V ÎtX	П.в.U,VÍ<X,tX>

2. ТЕСТ К - 2.

№	А	В	Дополнительная информация
	Идеальная с., элементами которой являются объекты к. K	С. объектов к. K, ObK	Понятия
	МорфизмA-1Î K(Y,X)ç A*A-1 = 1Y & A-1*A= 1X	Изоморфизм в к. K	Понятия
	Категория линейных пространств (л.п.) и линейных отображений (л.о.)	Категория топологических пространств (т.п.) и непрерывных отображений (н.о.)	Понятия
	Элементтопологии t	Открытое м.ux, содержащее точку х (т.е. xÎ ux Î t)	Понятия
	Последовательностьxn ½ n,m ® ¥ Þd(xn , xm ) ® 0	Сходящаяся к х последовательность, xn ® x	Понятия
	Подмножество Bx,r = {yÎX½ d(x,y) < r} Í X	Окрестность точки x, ux	Понятия
	Норма, || . ||	Длина вектора	Понятия
	Гомеоморфизм	Морфизм АÎT(X,Y)| $ A-1	Понятия
	А биекция	А изоморфизм в L	Пар. выс-я AÎL(X,Y)
	А изоморфизм в L	А изоморфизм в S	Пар. выс-я AÎL(X,Y)
	S(X,Y)	M(X,Y)	М-ва,X,YÎObM
	M(X,Y)	N(X,Y)	Категории

3. ТЕСТ К - 3.

№	А	В	Дополнительная информация
	Множество K(X, Y)всех морфизмов к. Kобъекта X в объект Y	Элемент с.ObS	Понятия
	Обратный морфизм в к. К, A-1	МорфизмA-1Î K(Y,X)ç A*A-1= 1Y & A-1*A= 1X	Понятия
	Категория топологических пространств (т.п.) и непрерывных отображений (н.о.)	Категория метрических пространств (м.п.) и непрерывных отображений (н.о.)	Понятия
	Открытое м. в т.п	Окрестность точки x, ux	Понятия
	Фундаментальная последовательность	Последовательностьxn ½ n,m ® ¥ Þd(xn , xm ) ® 0	Понятия
	Топология окрестностей в м.п. X, tO	Открытое м.ux, содержащее точку х (т.е. xÎ ux Î t)	Понятия
	Функция|| . ||: X ® [0, +¥) ½" x,yÎ X, l Î R(C) 1° || x || = 0 Û x = q 2° || lx || = ½l½ || x || 3° || x + y || £ || x || + || y ||	Норма, || . ||	Понятия
	Изоморфизмв категории T	Гомеоморфизм	Понятия
	A инъективен и сюръективен	А изоморфизм в S	Пар. выс-я AÎS(X,Y)
	M(X,Y)	N(X,Y)	М-ва,X,YÎObN
	L	S	Категории
	S	T(X,Y)	Категории

4. ТЕСТ К - 4.

№	А	В	Дополнительная информация
	Элемент м. K(X, Y)	Отображение A:X®Y	Понятия
	Отношение изоморфности объектов	Отношение эквивалентности	Понятия
	Категория метрических пространств (м.п.) и непрерывных отображений (н.о.)	Категория нормированных пространств (н.п.) и линейных непрерывных отображений (л.н.о.)	Понятия
	ОтображениеA:X®Y со свойством "(x Î X, uAx ÎtY ) $ vx ÎtX ½A(vx)ÍuAx	Непрерывное о., AÎ T(X,Y)	Понятия
	М.п., в котором " фундаментальная последовательность сходится (к некоторому x Î X)	Полное м.п.	Понятия
	Топология tO = {u Î Ã(X)½ x Î u Þ u Ê Bx,r для некоторого r> 0 }	Топология окрестностей в м.п. X, tO	Понятия
	Полное н.п.относительно метрики d(x,y) = || x - y ||	Банахово пространство (б.п.)	Понятия
	А изоморфизм в L	$ A-1 Î S(Y,X)	Пар. выс-я AÎL(X,Y)
	А изоморфизм в S	A инъекция	Пар. выс-я AÎS(X,Y)
	T(X,Y)	M(X,Y)	М-ва,X,YÎObM
	T	S	Категории
	N(X,Y)	N	Категории

5. ТЕСТ К - 5.

№	А	В	Дополнительная информация
	Отображение K(X,Y) ´ K(Y,Z) ® K(X,Z), обладающее свойствами: 1. Ассоциативность: C*(B*A) = (C*B)*A, 2. Существование единицы: " YÎObK$ 1YÎK(Y,Y)½ 1Y*A = A " A Î K(X, Y) & B*1Y = B " B Î K(Y, Z)	Правило композиции морфизмов в к. K, ComK	Понятия
	Бинарное отношениена ObK: X ~ Y Û $ изоморфизм A:X®Y	Рефлексивное, транзитивное, симметричное отношение	Понятия
	Категория T, для которой: ObTсостоит из всех т.п., T(X,Y)состоит из всех н.о. A:X®Y, ComT = ComS½T(X,Y) ´ T(Y,Z)(т.е. композиции и единицы в Tи Sсовпадают)	Категория	Понятия
	Упорядоченная пара <X, d>, где d -метрика во м. Х	Метрическое пространство (м.п.), Х	Понятия
	Полное м.п.	Банахово пространство	Понятия
	Относительная топология	Топология tO = {u Î Ã(X)½ x Î u Þ u Ê Bx,r для некоторого r> 0 }	Понятия
	Нормированное пространство (н.п.), Х	Полное н.п.относительно метрики d(x,y) = || x - y ||	Понятия
	$ A-1 Î S(Y,X)	А изоморфизм в M	Пар. выс-я AÎM(X,Y)
	А сюръекция	А изоморфизм в S	Пар. выс-я AÎS(X,Y)
	L(X,Y)	N(X,Y)	М-ва,X,YÎObN
	N	M	Категории
	ВA - морфизм к. L	АÎN(X,Y) и ВÎN(Y,Z)	П.в-я А,В - морфизмы к. S

6. ТЕСТ К - 6.

№	А	В	Дополнительная информация
	Бинарное отношениево м. всех категорий, которое задается отношениями: 1. ObP Í ObK 2. P(X,Y) Í K(X,Y)" X,Y Î ObP 3. ComP = ComK½P(X,Y) ´ P(Y,Z) (т.е. правила композиции в Kи Pсовпадают)	Рефлексивное, транзитивное, симметричное отношение	Понятия
	Категория S, для которой: ObSсостоит из всех м., S(X,Y)состоит из всех о. A:X®Y, ComSопределяется формулами: 1° (B*A)(x) = B[A(x)] 2° 1x(x) = x	Категория множеств и отображений, S	Понятия
	ОтображениеA:X®Y со свойством "(x Î X, uAx ÎtY ) $ vx ÎtX ½A(vx)ÍuAx	Непрерывное о., AÎ T(X,Y)	Понятия
	Нормированное пространство (н.п.), Х	Функциональное пространство с нормой	Понятия
	Непрерывное л.о. в н.п., A Î N(X,Y)	Отображение A:X®Y со свойством: (xÎX,xn®x)ÞAxn®Ax	Понятия
	А изоморфизм в T	$ A-1 Î S(Y,X)	Пар. выс-я AÎT(X,Y)
	А изоморфизм в S	А изоморфизм в M	Пар. выс-я AÎM(X,Y)
	S(X,Y)	N(X,Y)	М-ва,X,YÎObN
	T	N	Категории
	АÎN(X,Y) и ВÎN(Y,Z)	ВA - морфизм к. T	П.в-я А,В - морфизмы к. S
	ObS	Система л.п.	Системы
	U,V ÎtX	UÇV Î tX	П.в. <X,tX>, U,V Í X

7. ТЕСТ К - 7.

№	А	В	Дополнительная информация
	Множество K(X, Y)всех морфизмов к. Kобъекта X в объект Y	Элемент с.ObS	Понятия
	Категория множеств и отображений	Категория линейных пространств (л.п.) и линейных отображений (л.о.)	Понятия
	Открытое м. в т.п	Элементтопологии t	Понятия
	ОтображениеA:X®Y со свойством "(x Î X, uAx ÎtY ) $ vx ÎtX ½A(vx)ÍuAx	Непрерывное о., AÎ T(X,Y)	Понятия
	Нормированное пространство (н.п.), Х	Функциональное пространство с нормой	Понятия
	Полное н.п.относительно метрики d(x,y) = || x - y ||	Банахово пространство (б.п.)	Понятия
	$ A-1 Î S(Y,X)	А изоморфизм в M	Пар. выс-я AÎM(X,Y)
	T(X,Y)	M(X,Y)	М-ва,X,YÎObM
	Мн-во морфизмов N(X,Y)	S	Категории
	ObN	ObT	Системы
	ObS	S(X,Y)	М-ва,X,YÎObS
	||x||1	||x||2	Числа x=<1,1/2,1/3,...>

8. ТЕСТ К - 8.

№	А	В	Дополнительная информация
	Упорядоченная тройка <ObK, K(X, Y) "X,YÎObK, ComK>, где ObK- с. объектов к. K, K(X, Y) - м. морфизмов к. Кобъекта X в объект Y, ComK -правило композиции морфизмов в к. K	Категория (к.), K	Понятия
	Отношение “Pподкатегория K”	Рефлексивное, транзитивное, антисимметричное отношение	Понятия
	Категория множеств и отображений	Категория линейных пространств (л.п.) и линейных отображений (л.о.)	Понятия
	Подмножество t Í Ã(X) со свойствами: 1° {Æ, X} Í t 2° u, v Î tÞ u Ç v Ît 3° s Í t Þîþu Î t uÎs	Топология в Х, t	Понятия
	Сходящаяся к х последовательность, xn ® x	Последовательностьxn ½ n ® ¥ Þd(xn , x) ® 0	Понятия
	Шар (в м.п.), Bx,r	Подмножество Bx,r = {yÎX½ d(x,y) < r} Í X	Понятия
	Упорядоченная пара <X,|| . || >, где || . || -норма в л.п. Х	Нормированное пространство (н.п.), Х	Понятия
	ОтображениеA:X®Y с 2 свойствоми: 1° А непрерывно; 2° А линейно	Непрерывное л.о. в н.п., A Î N(X,Y)	Понятия
	А изоморфизм в T	A:X®Y - биекция	Пар. выс-я AÎT(X,Y)
	А изоморфизм в N	А изоморфизм в S	Пар. выс-я AÎN(X,Y)
	L(X,Y)	T(X,Y)	М-ва,X,YÎObL
	L	N(X,Y)	Категории

ã Калмыков А.А. 2005 m_k.doc