Уравнение неразрывности. В любом сечении стационарно текущей идеальной жидкости модуль скорости обратно пропорционален площади сечения.

Характеристики течения жидкостей и газов.

Уравнение неразрывности.

Жидкости и газы существенно отличаются друг от друга, в частности различие между ними обусловлено большой сжимаемостью газов и практически несжимаемостью жидкостей. Вместе с тем, многие явления в неподвижных жидкостях и газах, как мы в этом убедились ранее, аналогичны (например, законы Паскаля и Архимеда выполняются и для жидкостей и для газов).

Как показывает опыт, можно пренебречь сжимаемостью газов при их скоростях много меньших скорости звука (v << v_зв = 340 м/с).

В дальнейшем, говоря о динамике жидкостей, предполагается, что те же законы будут справедливы и для газов при v << v_зв.

Жидкость отличается от газа также наличием у нее сил внутреннего трения или вязкости.

Вязкостью называется свойство жидкостей оказывать сопротивление относительному перемещению своих частей.

Явления, связанные с вязкостью и сжимаемостью усложняют исследование движения жидкости. Поэтому будем пренебрегать этими явлениями.

Жидкость, вязкостью и сжимаемостью которой можно пренебречь, называется идеальной жидкостью.

Два основных типа течения жидкостей и газов.

1. Движение жидкости, при котором отдельные слои ее скользят друг относительно друга, не перемешиваясь, называется ламинарным течением.

2. Движение жидкости, сопровождающееся перемешиванием ее различных слоев с образованием завихрений, называется турбулентным (вихревым).

Ламинарное движение переходит в турбулентное с увеличением скорости течения жидкости. В дальнейшем будем рассматривать ламинарное течение.

Кинематическое описание движения жидкости.

Существуют два способа описания течения жидкостей.

1 способ. Метод Лагранжа. Движение жидкости описывается, как движение твердого тела, Для этого жидкость представляется, как совокупность большого числа малых точечных элементов, и записываются уравнения движения каждого такого элемента.

2 способ. Метод Эйлера. Рассматриваются изменения, происходящие в мысленно выделенной области пространства, неподвижной относительно данной системы отсчета. Для этого в некоторый момент времени измерим скорости малых элементов жидкости, оказавшихся в некоторых выделенных точках пространства, и будем затем следить, как с течением времени изменяется, (или не изменяется) скорость в этих выделенных точках пространства.

В дальнейшем, при описании движения жидкости будем пользоваться методом Эйлера.

Проведем в движущейся жидкости для любого фиксированного момента времени линии так, чтобы касательные к ним в каждой точке совпадали по направлению с вектором скорости частиц в данной точке. Такие линии называются линиями тока (рис. 5.3.1).

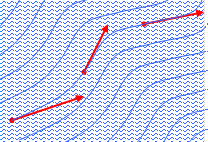
Рис. 5.3.1.

Если во всех точках пространства скорость элементов жидкости не меняется со временем, то такое движение жидкости называется стационарным или установившимся.

Часть жидкости, ограниченная линиями тока, называется трубкой тока.

Свойства линий тока стационарного течения жидкости.

1. Линии тока совпадают с траекториями частиц.

2. Линии тока не пересекаются друг с другом. В противном случае, в точке их пересечения скорость оказалась бы неоднозначной.

3. Через поверхность, образованную линиями тока не выйдет ни одна частица жидкости, находящаяся внутри такой трубки тока. В противном случае получим противоречие со вторым свойством.

Вывод уравнения неразрывности.Рассмотрим ламинарное стационарное течение жидкости. Выберем в жидкости трубку тока небольших поперечных размеров, таких, что скорость частиц жидкости во всех точках одного и того же сечения можно считать одинаковой (рис. 5.3.2).

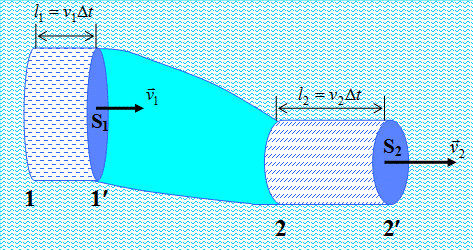
Рис. 5.3.2.

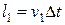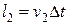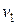За малый промежуток времени Dt масса жидкости, занимавшая объём между сечениями 1 и 2 оказалась в объёме между сечениями 1¢ и 2¢. Это означает, что жидкость в части трубки, имеющей сечение S₁, переместится на расстояние , а в части трубки сечением S₂ – на расстояние , где и 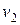– скорости частиц жидкости в различных частях трубки тока. Обозначив плотность жидкости в выбранных сечениях S₁ и S₂ через r₁ и r₂, получим уравнение сохранения массы при течении жидкости по трубке.

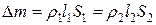. (5.3.1)

В случае идеальной (несжимаемой) жидкости ( 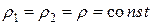) сохраняется объем переносимой жидкости:

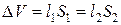, (5.3.2)

Þ .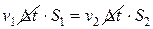

В результате получим уравнение неразрывности

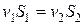, (5.3.3)

которое можно записать также в виде

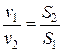(5.3.4)

или

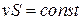. (5.3.5)

Уравнение неразрывности. В любом сечении стационарно текущей идеальной жидкости модуль скорости обратно пропорционален площади сечения.

Пример. Течение реки медленное, когда она разливается широка, и, наоборот, река течет быстрее в узком ущелье.