Примеры для самостоятельного решения. 12.4.1. Паропроводная труба диаметром 20 см защищена слоем магнезии толщиной 10 см

12.4.1. Паропроводная труба диаметром 20 см защищена слоем магнезии толщиной 10 см. Теплопроводность магнезии 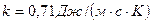. Допустив, что температура трубы 160° С, а внешней поверхности слоя магнезии 30 °С, найти распределение температуры внутри покрытия, а также количество теплоты, отдаваемое трубой в окружающую среду в течение суток на протяжении трубы в 1 м.

12.4.2. Толщина кирпичной стены 30 см; 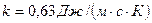. Установить, как зависит температура от расстояния от точки до наружного края стены, если температура равна 20 °С на внутренней и 0°С на внешней поверхности стены. Найти также количество теплоты, которое стена площадью 1 м² отдает в окружаю­щую среду в течение суток.

12.4.3. Согласно закону Ньютона, скорость охлаждения какого-либо тела в воздухе пропорциональна разности между температурой тела и температурой воздуха. Если температура воздуха равна 20°С и тело в течение 20 мин охлаждается от 100 до 60°С, то через какое время температура его понизится до 30 °С?

12.4.4.Определить время совершения преступления, если в момент обнаружения температура тела равнялась 31 °С, а час спустя составляла 29 °С (считать, что в момент смерти человека температура его тела равна 37 °С, а температура воздуха 21 °С).

12.4.5. Температура вынутого из печи хлеба в течение 20 мин понижается от 100 до 60°С. Температура окружающего воздуха 25 °С. Через какое время с момента начала охлаждения температура хлеба понизится до 30 °С?

Движение материальной точки

При решении задач ди­намики материальной точки используют второй закон Ньютона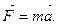

Решение типовых примеров

Пример 7. Материальная точка массой m с начальной скоростью 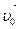движется прямолинейно. На точку действует сила сопротивления 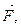направленная в сторону, противоположную направлению движения, и по модулю равная 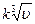(k-размерный постоянный коэффициент). Определить время 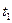от начала движения точки до остановки и путь s - пройденный точкой.

Решение. Примем за ось Ох прямую, вдоль которой происходит движение, а за начало координат - начальное положение точки. На точку действует только одна сила 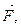следовательно, дифференциальное уравнение движения точки имеет вид

.

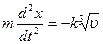Так как точка движется по прямой, то 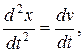и уравнение принимает вид

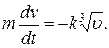
Его общее решение

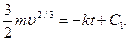
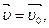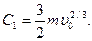Поскольку при t=0 то Следовательно, 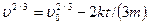Так как в момент t 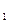(остановки точки) 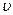= 0, то отсюда следует, что 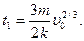Для того чтобы найти х как функцию t, полученное частное решение исходного уравнения перепишем в виде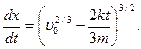

Проинтегрировав его, будем иметь

.

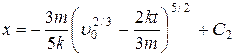Так как при 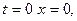то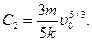

Таким образом,

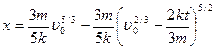
Следовательно, в момент остановки 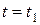пройденный путь

.
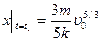