Конспект лекций по обыкновенным дифференциальным уравнениям. ч.3. 4 страница
которую будем называть соответствующей уравнению (1).
Задачи интегрирования уравнения (1) и системы (2) эквивалентны. Имеет место следующая
Теорема 1. Левая часть любого I-го интеграла системы (2) есть решение уравнения (1); обратно, всякое решение уравнения (1), приравненное произвольной постоянной, дает I-й интеграл системы (2).
Пусть
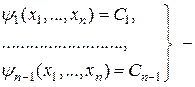
совокупность 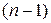 независимых I интегралов системы (2).
независимых I интегралов системы (2).
В пространстве с координатами 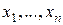 эта система интегралов определяет
эта система интегралов определяет 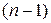 - параметрическое семейство линий – характеристик уравнения (1). Докажем сначала первое утверждение теоремы.
- параметрическое семейство линий – характеристик уравнения (1). Докажем сначала первое утверждение теоремы.
Вдоль любой интегральной кривой системы (2) имеем
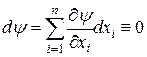 . (3)
. (3)
Но вдоль интегральной кривой системы (2) дифференциалы 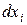 пропорциональны функциям
пропорциональны функциям 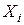 , следовательно, в силу однородности относительно
, следовательно, в силу однородности относительно 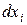 левой части тождеств
левой части тождеств
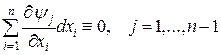
дифференциалы 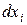 могут быть заменены пропорциональными им величинами
могут быть заменены пропорциональными им величинами 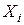 , при этом получим, что вдоль интегральных кривых системы (2)
, при этом получим, что вдоль интегральных кривых системы (2)
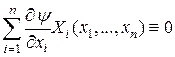 . (4)
. (4)
Интегральные кривые системы (2) проходят через каждую точку рассматриваемой области изменения независимых переменных 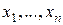 (в силу теоремы существования), и левая часть (4) не зависит от постоянных
(в силу теоремы существования), и левая часть (4) не зависит от постоянных 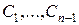 и, следовательно, не меняется при переходе от одной интегральной кривой к другой, значит, тождество (4) справедливо не только вдоль некоторой интегральной кривой, но и во всей рассматриваемой области изменения переменных
и, следовательно, не меняется при переходе от одной интегральной кривой к другой, значит, тождество (4) справедливо не только вдоль некоторой интегральной кривой, но и во всей рассматриваемой области изменения переменных 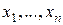 , а это и означает, что функция
, а это и означает, что функция 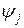 является решением исходного уравнения
является решением исходного уравнения
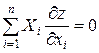 . (1)
. (1)
Обратно, пусть некоторая функция 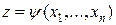 обращает уравнение (1) в тождество (во всей области изменения переменных
обращает уравнение (1) в тождество (во всей области изменения переменных 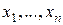 ):
):
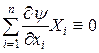 .
.
Поскольку вдоль любой интегральной кривой системы (2) 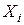 и
и 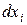 пропорциональны, то
пропорциональны, то
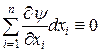 ,
,
а, следовательно, 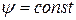 вдоль интегральной кривой, а это и значит (в силу теоремы единственности), что
вдоль интегральной кривой, а это и значит (в силу теоремы единственности), что 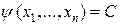 есть первый интеграл системы (2) (по определению). Ч.т.д.
есть первый интеграл системы (2) (по определению). Ч.т.д.
Теорема 2. 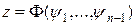 , где
, где 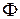 – произвольная дифференцируемая функция,
– произвольная дифференцируемая функция, 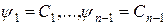 - независимые I-е интегралы системы (2), является общим решением уравнения (1), т.е. решением, содержащим все без исключения решения этого уравнения.
- независимые I-е интегралы системы (2), является общим решением уравнения (1), т.е. решением, содержащим все без исключения решения этого уравнения.
Пусть 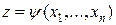 есть некоторое решение уравнения (1). Докажем, что существует функция
есть некоторое решение уравнения (1). Докажем, что существует функция 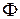 такая, что
такая, что 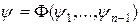 . Так как
. Так как 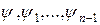 являются решениями уравнения (1), то
являются решениями уравнения (1), то
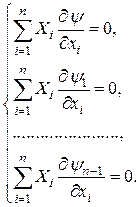 (5)
(5)
Эта система в каждой точке x 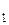 ,…,x
,…,x 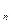 рассматриваемой области имеет нетривиальное решение, т.к.
рассматриваемой области имеет нетривиальное решение, т.к. 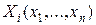 по предположению не обращаются в нуль одновременно. Поэтому определитель
по предположению не обращаются в нуль одновременно. Поэтому определитель
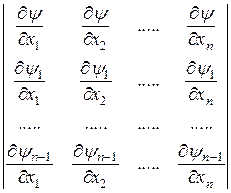
тождественно равен нулю в рассматриваемой области. Но это означает, что между функциями 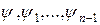 имеется функциональная зависимость
имеется функциональная зависимость
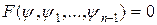 . (6)
. (6)
В силу независимости I-х интегралов 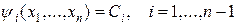 системы (2) по крайней мере один из миноров
системы (2) по крайней мере один из миноров 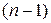 порядка якобиана
порядка якобиана
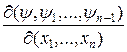
вида
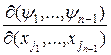
отличен от нуля. Следовательно, уравнение (6) можно представить в виде
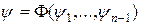 .
.
Ч.т.д.
Пример .
Проинтегрировать уравнение
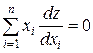 .
.
Система уравнений характеристик
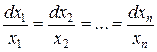
имеет следующие независимые первые интегралы
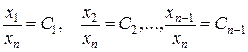 .
.
Общее решение исходного уравнения имеет, таким образом, следующий вид
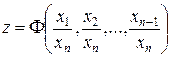
и является произвольной однородной функцией нулевой степени однородности.
6. Дифференциальные уравнения, допускающие понижение порядка.
6.1. Уравнения 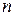 - го порядка, разрешаемые в квадратурах.
- го порядка, разрешаемые в квадратурах.
I. Уравнение вида
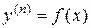 (1)
(1)
интегрируется в квадратурах:
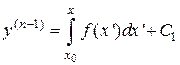 ,
,
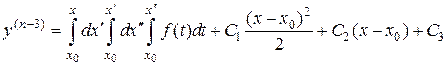 ,…
,…
………………………………………………………………….
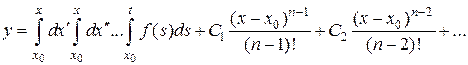
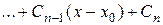 . (2)
. (2)
Формула (2) дает общее решение уравнения (1). Преобразуем первый член в формуле (2) справа. При 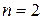 он имеет вид
он имеет вид
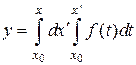 .
.
Воспользуемся формулой Дирихле
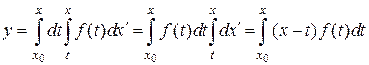 . (3)
. (3)
Пусть теперь 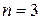 :
:
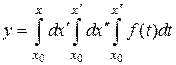 .
.
Внутренний двойной интеграл заменим по формуле (3)
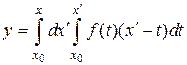 .
.
Теперь снова воспользуемся формулой Дирихле
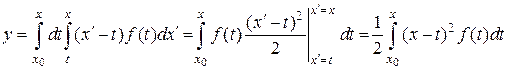 .
.
Пусть для 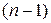 справедлива формула
справедлива формула
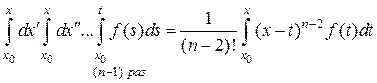 .
.
Тогда получаем
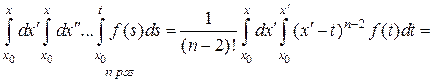
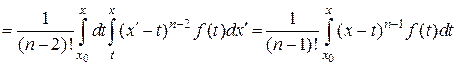 .
.
Итак, окончательно имеем для любого натурального 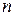 :
:
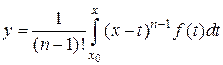 . (4)
. (4)
Это формула Коши. Формула (4) дает частное решение уравнения (1), удовлетворяющее нулевым начальным данным
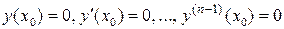 ,
,
а в совокупности с (2) имеем общее решение.
Если дано уравнение вида
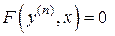 , (5)
, (5)
то, разрешив его относительно 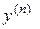 , получим уравнение вида (1), но иногда это уравнение лишь позволяет выразить
, получим уравнение вида (1), но иногда это уравнение лишь позволяет выразить 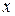 и
и 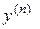 как функции некоторого параметра
как функции некоторого параметра 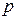 . Пусть эти параметрические уравнения имеют вид
. Пусть эти параметрические уравнения имеют вид
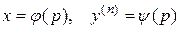 . (6)
. (6)
По определению
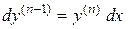 ,
,
т.е. с учетом (6)
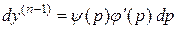 ,
,
откуда
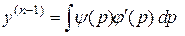 ,
,
далее
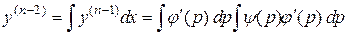
и т.д. В результате получим
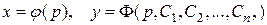 .
.
Исключив из последних соотношений 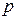 , получим общий интеграл уравнения (5).
, получим общий интеграл уравнения (5).
Замечание. Рассматривая (6) как замену переменных, можно воспользоваться формулой Коши (4):
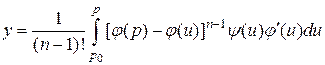 , (7)
, (7)
где 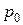 соответствует
соответствует 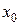 , а
, а 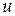 соответствует
соответствует  . Вместо
. Вместо 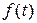 в (7) подставлено
в (7) подставлено 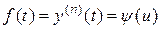 .
.
Пример.
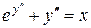 .
.
Полагаем 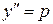 , тогда
, тогда 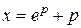 . Отсюда
. Отсюда
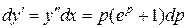 ,
,
т.е.
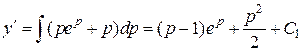 ,
,
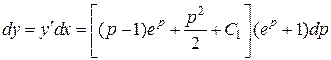 ,
,
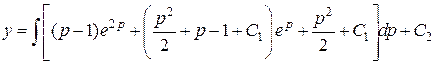 ,
,
или
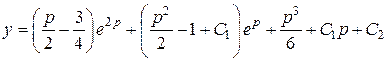 .
.
Эта формула вместе с формулой 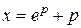 дает параметрическое представление общего решения уравнения.
дает параметрическое представление общего решения уравнения.
II. Уравнение вида
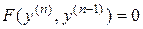 (8)
(8)
также приводится к квадратурам.
Пусть сначала уравнение (8) разрешено относительно 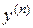 , т.е.
, т.е.
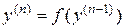 . (8а)
. (8а)
Полагая 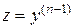 , имеем
, имеем
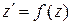 .
.
Отсюда получаем
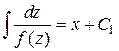 .
.
Пусть это соотношение разрешено относительно 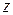 , т.е.
, т.е.
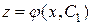 ,
,
тогда
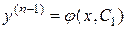 .
.
В соответствии с предыдущим
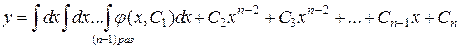 .
.
Если же уравнение (8) неразрешимо в явном виде, но можно ввести параметр  , так, что
, так, что
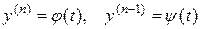 , (8б)
, (8б)
то тогда имеем 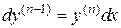 , или
, или 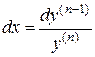 , т.е.
, т.е. 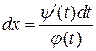 , откуда для
, откуда для 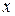 получаем
получаем
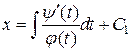 .
.
Далее, последовательно
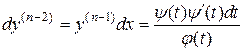 ,
,
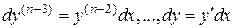 ,
,
и, наконец,
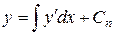 .
.
III. Уравнение вида
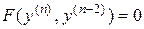 (9)
(9)
сводится к предыдущим случаям.
Положим 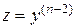 , тогда имеем
, тогда имеем
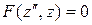 . (10)
. (10)
Если уравнение (10) разрешено относительно 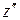 :
:
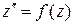 , (10а)
, (10а)
то перепишем его в виде
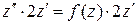 ,
,
т.е.
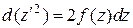 ,
,
откуда
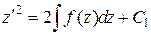 .
.
Теперь
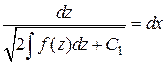 .
.
Откуда общий интеграл уравнения (10а):
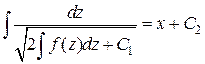 .
.
Т.к. 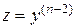 , то полученное выражение принимает вид
, то полученное выражение принимает вид
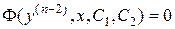 ,
,
а это – уравнение вида (5), т.е. оно интегрируется.
Если же уравнение (9) приводится к виду
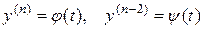 , (9а)
, (9а)
то действуем следующим образом:
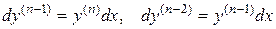 .
.
Исключая 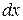 , получим
, получим
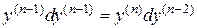 .
.
Откуда в силу (9а):
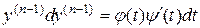 ,
,
т.е.
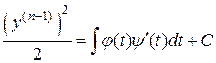 ,
,
т.е.
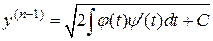 .
.
Имея параметрические представления 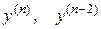 , мы свели задачу к виду (8б).
, мы свели задачу к виду (8б).
6.2. Уравнения, допускающие понижение порядка.
I. Уравнение вида
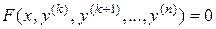 (11)
(11)
заменой 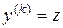 приводится к виду
приводится к виду
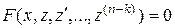 (11а)
(11а)
порядка 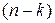 . Уравнение
. Уравнение 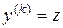 решается в квадратурах (см. выше).
решается в квадратурах (см. выше).
II. Уравнение вида
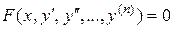 . (12)
. (12)
Здесь полагают: 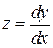 , за независимую переменную принимают
, за независимую переменную принимают 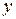 . Тогда
. Тогда
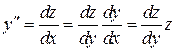 ,
,
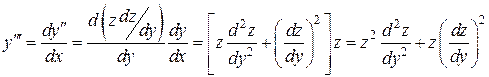 .
.
Легко доказать методом полной индукции, что 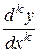 выражается через
выражается через 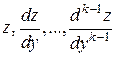 . Подставляя выражения для
. Подставляя выражения для 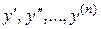 в новых переменных в уравнение (12), получим новое дифференциальное уравнение
в новых переменных в уравнение (12), получим новое дифференциальное уравнение 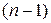 - го порядка
- го порядка
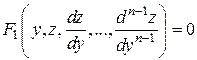 ,
,
т.е. порядок уравнения понижен на единицу.
6.2.1. Понижение порядка в однородных уравнениях.
I. Рассмотрим уравнение вида
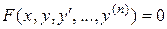 , (13)
, (13)
в котором 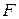 - однородная функция от
- однородная функция от 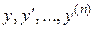 , т.е.
, т.е.
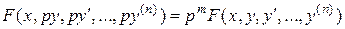 (14)
(14)
для любого 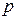 ,
, 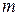 - порядок однородности.
- порядок однородности.
Из (14) следует, что если 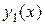 - решение уравнения (13), то и
- решение уравнения (13), то и 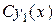 - также является решением уравнения (13).
- также является решением уравнения (13).
Введем новую неизвестную функцию при помощи соотношения
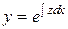 . (15)
. (15)
Тогда
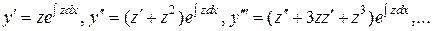
и вообще 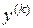 выражается в виде произведения
выражается в виде произведения 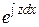 на выражение, содержащее
на выражение, содержащее 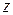 и его производные до
и его производные до 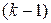 - го порядка. Подставим эти выражения в (13) и учтем (14):
- го порядка. Подставим эти выражения в (13) и учтем (14):
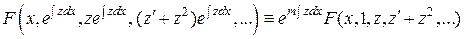 .
.
Отбрасывая множитель 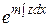 , получим уравнение порядка
, получим уравнение порядка 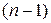 :
:
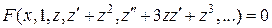 .
.
Найдя 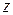 , будем иметь
, будем иметь
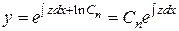 .
.
Пример.
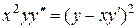 -
-
однородное уравнение II-го порядка. Подставляя 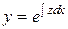 , получим:
, получим:
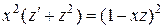 ,
,
т.е. 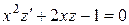 - линейное уравнение. Его решение, например, методом Даламбера
- линейное уравнение. Его решение, например, методом Даламбера
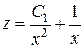 ,
,
откуда
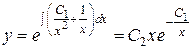 .
.
II. Уравнения, однородные относительно 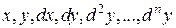 .
.
Запишем уравнение (13) в следующем виде
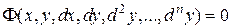 . (16)
. (16)
Это однородное уравнение, если
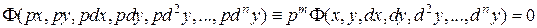 (17)
(17)
Это уравнение не изменится, если заменить 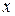 на
на 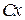 , а
, а 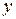 на
на 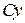 , где
, где 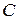 - постоянная. Введем новые переменные при помощи соотношений
- постоянная. Введем новые переменные при помощи соотношений
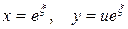 .
.
Тогда
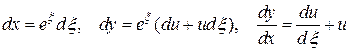 .
.
Далее,
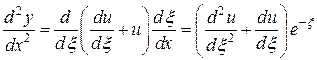 ,
,
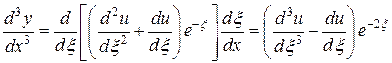 ,…
,…
Итак, мы имеем
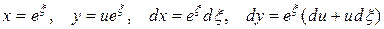 ,
,
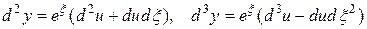 ,… (18)
,… (18)
(при этом 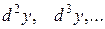 взяты в предположении, что независимая переменная есть
взяты в предположении, что независимая переменная есть 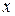 , а
, а 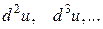 - в предположении, что независимая переменная есть
- в предположении, что независимая переменная есть 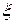 ).
).
Подставим (18) в (16), воспользуемся (17) и сократим на 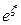 , тогда получим
, тогда получим
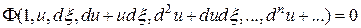 .
.
Мы получили уравнение 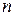 - го порядка, которое явно не содержит независимую переменную
- го порядка, которое явно не содержит независимую переменную 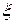 . Замена
. Замена 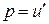 позволяет понизить его порядок на единицу.
позволяет понизить его порядок на единицу.
III. Уравнения, левая часть которых является точной производной.
Пусть в уравнении (13)
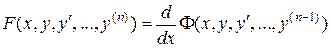 ,
,
т.е.
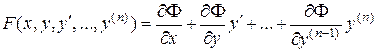 , (19)
, (19)
тогда каждое решение уравнения (13) является решением дифференциаль-ного уравнения
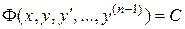
и обратно. Таким образом, соотношение (19) является первым интегралом уравнения (13), т.е его порядок понижен на единицу.
Пример.
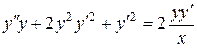 .
.
Разделим обе части уравнения на 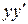 :
:
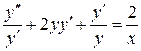 .
.
Первый интеграл:
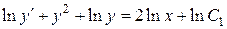 ,
,
т.е.
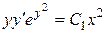 .
.
Здесь снова, интегрируя, получим
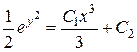 ,
,
т.е. 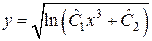 .
.
Список литературы
[1] В.В. Степанов. Курс дифференциальных уравнений. М.: ГИТТЛ, 1953г.
[2] А.Н.Тихонов, А.Б.Васильева, А.Г.Свешников. Дифференциальные уравнения. М.: Наука. Физматлит, 1998.
[3] Л.Э.Эльсгольц. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1965 г.
[4] Р.Беллман. Введение в теорию матриц. М.: Наука, 1978г.
[5] Л.С.Понтрягин. Обыкновенные дифференциальные уравнения. Москва-Ижевск: РХД, 2001г.
[6] В.Ф.Филиппов. Сборник задач по обыкновенным дифференциальным уравнениям. М.:Наука, 1990г.
[7] Сборник задач по математике для ВТУЗов. Под редакцией А.В.Ефимова, Б.П.Демидовича. Т.2. М.:Наука, 1995 г.
[8] А.Г.Кюркчан, Н.И.Смирнова. Конспект лекций по обыкновенным дифференциальным уравнениям. Ч.1. М.: МТУСИ, 2007, Ч.2. М.: МТУСИ, 2010.
План УМД 2010-2011 уч. г., п.
Александр Гаврилович Кюркчан
Надежда Ивановна Смирнова
