Разложение функций в степенные ряды 2 страница

Поэтому если взять 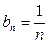, то окажется 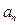~ 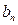, что обеспечит в дальнейшем выполнение условия (6). Поэтому проведем сравнение (в предельной форме) ряда (8) с гармоническим рядом 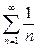, который, является рядом вида (7) при 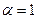, а потому расходится. Для проверки выполнения условия (6) вычислим предел:

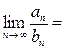
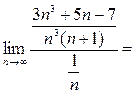
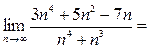
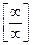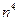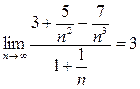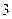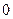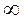={делим числитель и знаменатель на }= . Поскольку число – это не и не , то по признаку сравнения в предельной форме ряд (8) ведет себя (в смысле сходимости-расходимости) так же, как и гармонический. Но гармонический ряд – расходится, следовательно, ряд (8) тоже расходится.

Пример 3. Исследовать сходимость ряда

(9) .

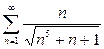Решение. Опять сравним (в предельной форме) ряд (9) с рядом вида (7) с подходящим значением параметра 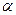. Для его выбора опять оценим поведение общего члена 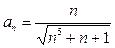, оставляя в числителе и знаменателе только старшие степени :

~ .

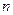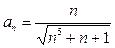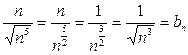Поэтому сравним (в предельной форме) ряд (9) с рядом 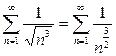. Этот ряд сходится, так как это ряд вида (7) при 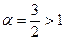. В нашем примере ряд (2) есть ряд (9) (а потому 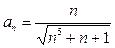), а ряд (3) есть сходящийся ряд 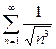(а потому 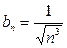) . Вычислим предел (6):

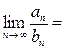
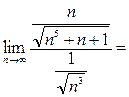
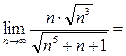
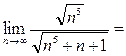
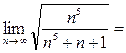
= {делим числитель и знаменатель на 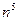}= 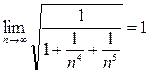. Поскольку число 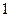– это 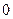не и не 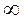, то по признаку сравнения в предельной форме ряд (9) ведет себя так же, как и сходящийся ряд 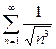. Поэтому ряд (9) тоже сходится.

Перейдем к другой группе признаков сходимости-расходимости положительных рядов. Их преимущество состоит в том, что для их применения не надо строить вспомогательные ряды, как это необходимо при применении признаков сравнения рядов.

Теорема (признак Даламбера). Пусть для положительного ряда 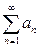существует предел

(10) .

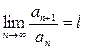Тогда при l > 1 ряд расходится, а при l < 1 сходится.

В выражении (10): 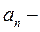общий член исследуемого ряда, а выражение для 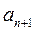получается из выражения для 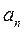заменой в нем 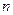на 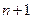. Доказательство признака Даламбера построено на сравнении ряда 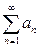со специально построенной сходящейся (в случае l < 1) или расходящейся (в случае l > 1) геометрической прогрессией. Оно достаточно формализовано, а потому мы его опускаем.

Большим недостатком признака Даламбера является то, что он не отвечает на вопрос о сходимости-расходимости в случае 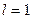(что встречается достаточно часто) и тогда требуется дополнительное исследование. Например, такая ситуация возникает при исследовании гармонического ряда, да и вообще рядов вида 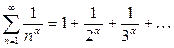, сходимость которых в зависимости от значения параметра 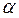обсуждалась выше.

Пример 4. Исследовать сходимость ряда

(11) .

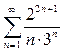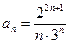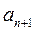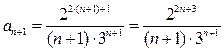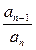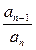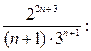
Решение. Общий член ряда (11) имеет вид . Тогда выражение для имеет вид: . Тогда их отношение равно : = = 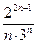=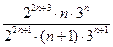{при делении степеней с одинаковым основанием показатели вычитаются}= 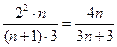. Вычисляем предел (10):

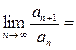
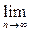
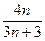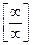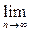
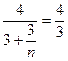= = . Итак, в (10) 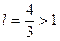, а потому по признаку Даламбера ряд (11) расходится.

Для дальнейших примеров напомним понятие факториала числа. Пусть 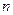− натуральное число (т.е. целое положительное). Тогда факториалом этого числа (обозначается 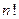) называется произведение всех целых чисел от 1 до этого числа :

.

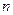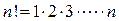Например, 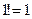, , 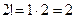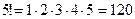. Факториалом числа ноль называется число 1: .

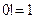Пример 5. Исследовать сходимость ряда .

(12) .

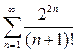Решение. Общий член ряда (12) имеет вид 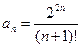. Тогда выражение для 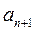имеет вид: 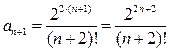. Тогда их отношение 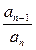равно : = = =
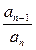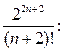
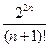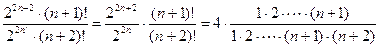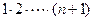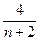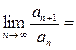
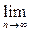
={сокращаем в числителе и знаменателе }= . Вычисляем предел (10): 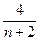= 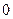. Итак, в (10) 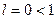, а потому по признаку Даламбера ряд (12) сходится.

Признак Даламбера удобно использовать для выяснения сходимости таких рядов, общие члены которых содержат степени (с постоянным основанием) и факториалы. В этом случае в выражении 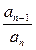многое сокращается (как это было видно на примерах), а само выражение оказывается достаточно простым для последующего вычисления предела 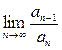. В некоторых других случаях удобно использовать следующий ниже признак.

Теорема (радикальный признак Коши). Пусть для положительного ряда 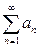существует предел

(13) .

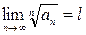Тогда при l > 1 ряд расходится, а при l < 1 сходится.

Аналогичным недостатком этого признака является то, что он не отвечает на вопрос о сходимости в случае 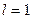и тогда требуется дополнительное исследование.

Пример 6. Исследовать сходимость ряда

(14) .

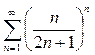Решение. Общий член ряда (14) имеет вид 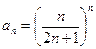. Вычислим предел (13):

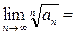
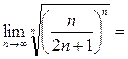
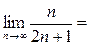
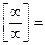
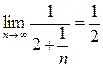. Итак, для предела (13) получилось 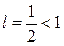, а потому по радикальному признаку Коши ряд (14) сходится.

Пример 7. Исследовать сходимость ряда

(15) .

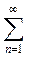
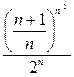Решение. Общий член ряда (15) имеет вид 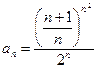. Вычислим предел (13):

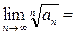
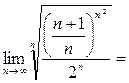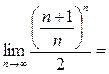
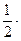
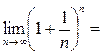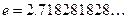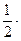
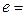
{извлекаем корень из числителя и знаменателя}= = {полученный предел представляет собой как раз второй замечательный предел, определяющий знаменитое число }= 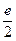Итак, для предела (13) получилось 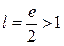, а потому по радикальному признаку Коши ряд (15) расходится.

Признак Коши удобно использовать для выяснения сходимости таких рядов, общий член которых 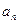является n-ой степенью некоторого несложного выражения. В этом случае в выражении 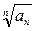корень и степень «сокращаются», а полученное выражение оказывается достаточно простым для последующего вычисления предела (13). В некоторых более сложных случаях удобно использовать следующий ниже признак.

Теорема (интегральный признак Коши). Пусть для положительного ряда 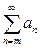(индекс суммирования 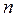может начинаться с любого целого числа 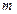) существует такая положительная непрерывная и убывающая на [m, +∞) функция 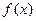, что 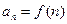. Тогда для сходимости этого ряда необходимо и достаточно, чтобы сходился несобственный интеграл .

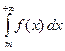Для применения этого признака функция 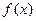, фигурирующая в теореме, может быть построена следующим образом: в выражении для общего члена ряда 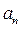букву 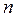заменяют на .

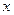Только этот признак из приведенных выше сможет ответить на вопрос о сходимости гармонического ряда и вообще рядов вида (7), что видно из следующего примера.

Пример 8. Исследовать сходимость ряда

(16)

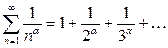
в зависимости от величины параметра .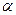

Решение. Если 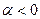, то общий член ряда 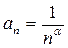не стремится к нулю (он будет даже стремиться к бесконечности), а потому по сформулированному в предыдущем параграфе признаку расходимости ряда этот ряд расходится. Рассмотрим теперь числа 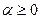. Общий член ряда (16) имеет вид 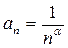. Заменяя в этом выражении 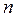на 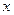, получим функцию 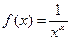, для которой, очевидно, выполнено: 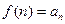. Проверим для нее выполнение условий интегрального признака Коши: функция 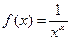должна быть положительной, непрерывной и убывающей на [1, +∞). Очевидно, все эти свойства выполняются в рассматриваемом случае 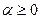. Поэтому по интегральному признаку Коши сходимость ряда (16) совпадает со сходимостью несобственного интеграла 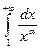. При рассмотрении темы «Несобственные интегралы» в качестве примера исследовалась сходимость именно этого интеграла и было выяснено, что он сходится для всех 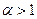и расходится для 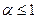. Таким образом, как это и утверждалось выше, ряд вида (16) сходится для всех 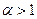и расходится для .

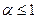Пример 9. Исследовать сходимость ряда

(17) .

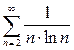Решение. Суммирование начато с 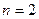, поскольку при 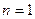общий член ряда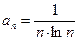 неопределен (деление на 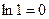). Общий член ряда (17) имеет вид 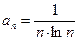. Заменяя в этом выражении 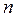на 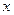, получим функцию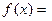 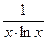, для которой, очевидно, выполнено: 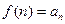. Далее, очевидно, что эта функция положительна, непрерывна и является убывающей на [2, +∞) (последнее следует из очевидного факта, что функция 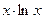положительная и возрастающая). Поэтому по интегральному признаку Коши сходимость ряда (17) совпадает со сходимостью несобственного интеграла 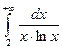. Исследуем этот интеграл на сходимость. Сходимость этого несобственного интеграла (по определению сходимости) зависит от того, будет ли существовать конечный предел

(18) .

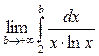Вычислим значение интеграла под знаком предела методом замены переменной:

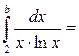
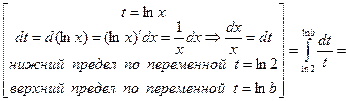
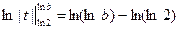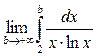
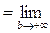
. Таким образом, предел в (18): 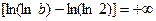. Поэтому по интегральному признаку Коши ряд (17) расходится.

Замечание. Легко теперь установить (по тому же интегральному признаку Коши), что «чуть исправленный» ряд 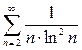уже сходится.

Знакочередующиеся ряды

Мы рассматривали признаки сходимости положительных рядов, все члены которых неотрицательны. Теперь мы будем допускать и отрицательные слагаемые, но для начала будем считать, что знаки слагаемых строго чередуются. Знакочередующимся рядом называется ряд, знаки слагаемых которого строго чередуются, начиная с положительного или отрицательного слагаемого. Поскольку число 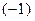в четной степени равно 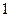, а в нечетной 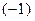, то такие ряды можно записать в форме

(1)

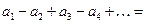
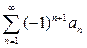
или

(2) ,

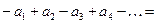
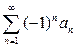причем в (1) и (2) уже считаем 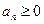, так как знак слагаемых мы учли множителем 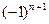или 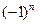. Эти множители попеременно принимают значения 1 и (−1), обеспечивая чередование знаков слагаемых рядов (1) и (2). Для обоснования сходимости таких рядов чаще всего используется так называемый признак Лейбница.

Теорема (признак Лейбница сходимости знакочередующихся рядов). Пусть для знакочередующегося ряда (1) или (2) выполнено:
1. Последовательность {a_n} монотонно убывает, т.е. .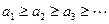
2. .
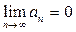Тогда исходный знакочередующийся ряд сходится.

Это только достаточный признак сходимости знакочередующихся рядов. Поэтому если для какого-либо знакочередующегося ряда условия признака не выполнены, это не означает, что этот ряд обязательно расходится. Однако если условия выполнены, то ряд обязательно сходится. Впрочем, понятно, что второе-то условие ( 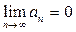) является необходимым для сходимости рядов вида (1) или (2), иначе общие члены этих рядов 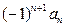и 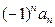не стремились бы к 0 тоже, а потому ряды бы оказались расходящимися (см. признак расходимости ряда в параграфе «Числовые ряды – основные понятия»).

Таким образом, справедливо следующее

Утверждение (достаточное условие расходимости знакочередующегося ряда). Если для знакочередующегося ряда (1) или (2)

(3) 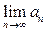или не существует, или ,

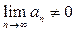то он является расходящимся.

Пример 1. Попробуем через один поменять знаки слагаемых у гармонического ряда 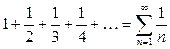(который, как известно, расходится). Получим следующий знакочередующийся ряд: 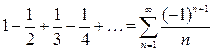. Это знакочередующийся ряд вида (1), для которого 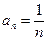и оба условия признака Лейбница, очевидно, выполняются. Действительно, очевидно, что последовательность 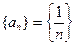убывает (с ростом номера n) и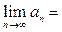 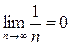. Поэтому этот ряд ( в отличие от гармонического ) сходится.

Пример 2. Исследовать на сходимость ряд

(4) .

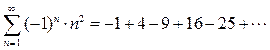Решение. Это знакочередующийся ряд вида (2), у которого 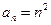. Очевидно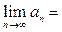 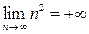, а потому выполнено условие (3) расходимости ряда. Итак, ряд (4) расходится.

Пример 3. Исследовать на сходимость ряд

(5) .

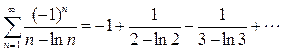Решение. Покажем, что ряд (5) является знакочередующимся рядом 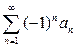с

(6)

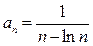
и к нему применим признак Лейбница. Для того, чтобы доказать, что ряд (5) является знакочередующимся, нужно показать, что в (6)

(7) .

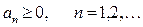Затем, чтобы показать, что к ряду (5) применим признак Лейбница, нужно доказать, что

(8)

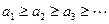
(9) .

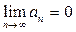Для доказательства свойств (7), (8) и (9) рассмотрим вспомогательную функцию

(10) , .

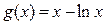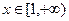Функция 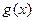в (10) это знаменатель в (6), где 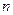заменено на 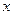. Ясно, что производная 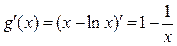, а потому 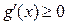для всех 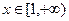, что влечет возрастание функции 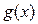на 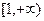. Но поскольку 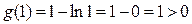, то и для всех 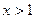выполнено 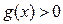. Отсюда сразу следует справедливость (7) (так как в (6) числитель равен 1, а знаменатель больше нуля) и (8) (так как в (6) числитель не меняется, а знаменатель растет). Покажем выполнение свойства (9):