Теорема о существовании и единственности решения Задачи Коши (3.2),(3.4). 3 страница
 .
.
Приравнивая коэффициенты при одинаковых степенях  в обеих частях последнего равенства, получим систему из трех уравнений с тремя неизвестными
в обеих частях последнего равенства, получим систему из трех уравнений с тремя неизвестными 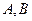 и
и 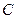 .
.
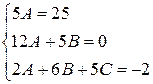
Откуда  . Поэтому
. Поэтому  , а общее решение данного уравнения:
, а общее решение данного уравнения: 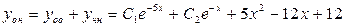 .
.
3.15). Решить уравнение 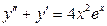 .
.
Решение. Сначала решим соответствующее однородное уравнение: 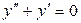 . Его характеристическое уравнение
. Его характеристическое уравнение 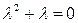 , или
, или  , имеет корни
, имеет корни  . Поэтому общее решение однородного уравнения записывается так:
. Поэтому общее решение однородного уравнения записывается так: 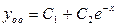 . Так как число
. Так как число 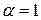 не является корнем характеристического уравнения, то в соответствии с разделом II (1) Таблицы 3 частное решение данного уравнения имеет вид
не является корнем характеристического уравнения, то в соответствии с разделом II (1) Таблицы 3 частное решение данного уравнения имеет вид 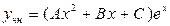 . Для нахождения коэффициентов
. Для нахождения коэффициентов 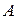 ,
, 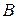 и
и 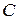 подставим эту функцию и ее производные в исходное уравнение. Сократив обе его части на
подставим эту функцию и ее производные в исходное уравнение. Сократив обе его части на 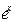 , имеем
, имеем 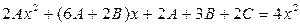 .
.
Приравнивая коэффициенты при одинаковых степенях  в левой и правой частях последнего равенства, получаем систему линейных уравнений для нахождения коэффициентов
в левой и правой частях последнего равенства, получаем систему линейных уравнений для нахождения коэффициентов 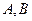 и
и 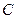
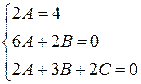 ,
,
решая которую, находим 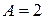 ,
,  ,
, 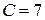 . Итак,
. Итак, 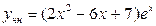 . По формуле (3.27) общее решение
. По формуле (3.27) общее решение 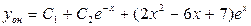 .
.
3.16). Решить уравнение  .
.
Решение. Соответствующее однородное уравнение: 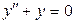 . Его характеристическое
. Его характеристическое 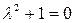 имеет корни
имеет корни 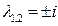 (Таблица 2 , раздел 3). Поэтому
(Таблица 2 , раздел 3). Поэтому 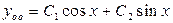 . По виду правой части, так как
. По виду правой части, так как 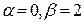 и числа
и числа 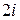 нет среди корней характеристического уравнения, частное решение записывается так
нет среди корней характеристического уравнения, частное решение записывается так 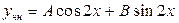 . Подставляя эту функцию и ее вторую производную в исходное уравнении, получим
. Подставляя эту функцию и ее вторую производную в исходное уравнении, получим 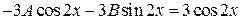 . Отсюда
. Отсюда 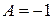 ,
, 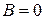 а значит
а значит 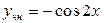 . Общее решение данного уравнения имеет вид
. Общее решение данного уравнения имеет вид 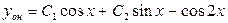 .
.
3.17) Решить уравнение  .
.
Решение. Однородное уравнение, соответствующее данному неоднородному, выглядит так 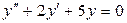 . Его характеристическое
. Его характеристическое 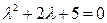 имеет корни
имеет корни 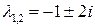 . Поэтому
. Поэтому 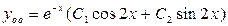 (Таблица 2 , раздел 3). По виду правой части, где
(Таблица 2 , раздел 3). По виду правой части, где 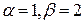 и числа
и числа 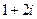 нет среди корней характеристического уравнения (Таблица 3, IV(1)), записываем частное решение неоднородного уравнения
нет среди корней характеристического уравнения (Таблица 3, IV(1)), записываем частное решение неоднородного уравнения 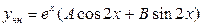 .
.
Подставляя эту функцию и ее производные в исходное уравнение, получим
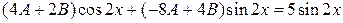 . Отсюда
. Отсюда  ;
; 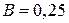 . Значит
. Значит
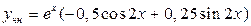 . Таким образом, общее решение данного уравнения имеет вид
. Таким образом, общее решение данного уравнения имеет вид 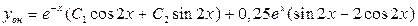 .
.
Задания для самостоятельного решения.
3.53. 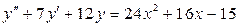 . 3.54.
. 3.54. 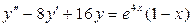 .
.
3.55. 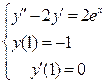 . 3.56.
. 3.56. 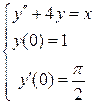 .
.
3.57. 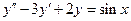 . 3.58.
. 3.58. 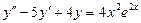 . 3.59.
. 3.59. 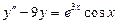 . .
. .
3.60. 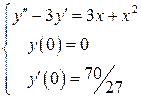 . 3.61.
. 3.61. 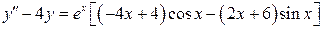 .
.
3.62.  . 3.63.
. 3.63. 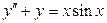 .
.
Ответы
3.53.  . 3.54.
. 3.54. 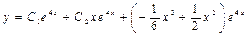 3.55.
3.55.  . 3.56.
. 3.56.  . 3.57.
. 3.57.  . 3.58.
. 3.58. 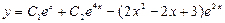
3.59. 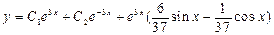 .
.
3.60. 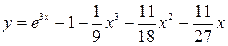 . 3.61.
. 3.61. 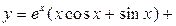
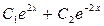 .
.
3.62. 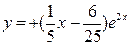 . 3.63.
. 3.63. 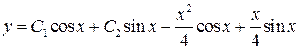 .
.
Контрольная работа № 3. Дифференциальные уравнения.
1.- 8. Определить тип и найти общие решения следующих дифференциальных уравнений.
- Решить задачу Коши.
3. Решить методом вариации произвольной постоянной.
4. Решить методом подстановки.
6. Решить уравнение, понижая его порядок.
8. Получить общее решение уравнения, записав вид его частного решения с неопределенными коэффициентами, не вычисляя их.
Вариант 1.
1.  . 2.
. 2.  . 3.
. 3. 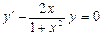 .
.
4.  . 5.
. 5. 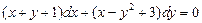 . 6.
. 6. 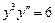 .
.
7. 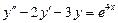 . 8.
. 8. 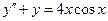 .
.
Вариант 2.
1. 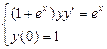 . 2.
. 2. 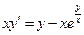 . 3.
. 3. 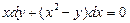 .
.
4.  . 5.
. 5. 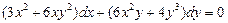 . 6.
. 6.  .
.
7.  . 8.
. 8. 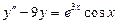 .
.
Вариант 3.
1. 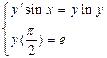 . 2.
. 2.  . 3.
. 3. 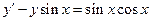 .
.
4. 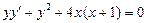 . 5.
. 5. 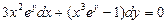 . 6.
. 6. 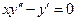 .
.
7. 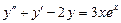 . 8.
. 8.  .
.
Вариант 4.
1. 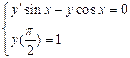 . 2.
. 2. 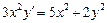 . 3.
. 3. 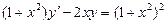 .
.
4. 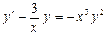 . 5.
. 5. 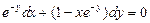 . 6.
. 6.  .
.
7. 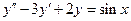 . 8.
. 8. 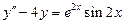 .
.
Вариант 5.
1. 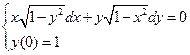 . 2.
. 2. 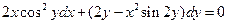 . 3.
. 3. 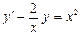 .
.
4.  . 5.
. 5. 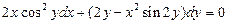 . 6.
. 6. 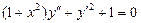 .
.
7. 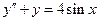 . 8.
. 8. 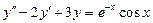 .
.
Вариант 6.
1. 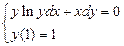 . 2.
. 2. 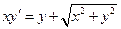 . 3.
. 3. 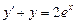 .
.
4. 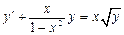 . 5.
. 5. 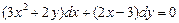 . 6.
. 6. 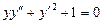 .
.
7. 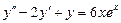 . 8.
. 8.  .
.
Вариант 7.
1. 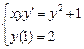 . 2.
. 2.  . 3.
. 3. 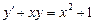 .
.
4. 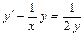 . 5.
. 5. 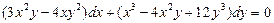 . 6.
. 6. 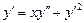 .
.
7. 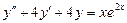 . 8.
. 8. 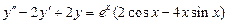 .
.
Вариант 8.
1. 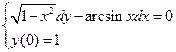 . 2.
. 2. 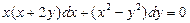 . 3.
. 3. 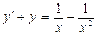 .
.
4. 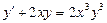 . 5.
. 5. 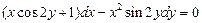 . 6.
. 6.  .
.
7. 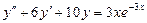 . 8.
. 8. 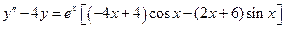 .
.
Вариант 9.
1. 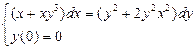 2.
2. 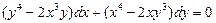 . 3.
. 3.  .
.
4.  . 5.
. 5. 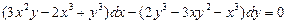 . 6.
. 6. 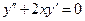 .
.
7. 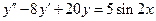 . 8.
. 8. 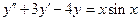 .
.
Вариант 10.
1. 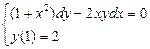 . 2.
. 2. 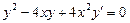 . 3.
. 3. 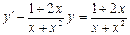 .
.
4. 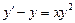 . 5.
. 5. 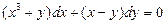 . 6.
. 6. 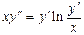 .
.
7. 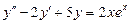 . 8.
. 8. 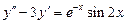 .
.
Вариант 11.
1. 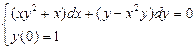 . 2.
. 2. 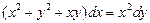 . 3.
. 3. 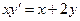 .
.
4. 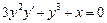 . 5.
. 5. 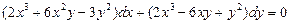 . 6.
. 6. 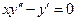 .
.
7. 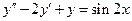 . 8.
. 8. 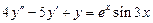 .
.
Вариант 12.
1. 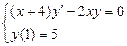 . 2.
. 2. 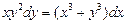 . 3.
. 3. 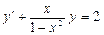 .
.
4.  . 5.
. 5. 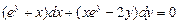 . 6.
. 6. 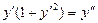 .
.
7. 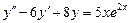 . 8.
. 8. 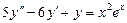 .
.
Вариант 13.
1.  . 2.
. 2. 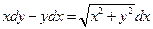 . 3.
. 3. 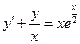 .
.
4. 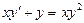 . 5.
. 5. 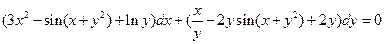 . 6.
. 6. 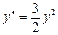 .
.
7. 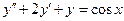 . 8.
. 8. 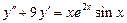 .
.
Вариант 14.
1.  . 2.
. 2. 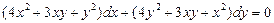 . 3.
. 3. 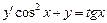 .
.
4. 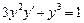 . 5.
. 5. 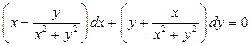 . 6.
. 6. 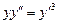 .
.
7. 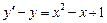 . 8.
. 8.  .
.
Вариант 15.
1. 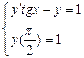 . 2.
. 2. 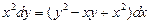 . 3.
. 3. 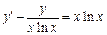 .
.
4. 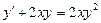 . 5.
. 5. 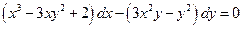 . 6.
. 6.  .
.
7. 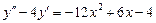 . 8.
. 8.  .
.
Вариант 16.
1. 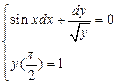 . 2.
. 2. 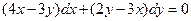 . 3.
. 3. 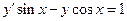 .
.
4. 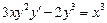 . 5.
. 5. 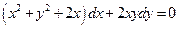 . 6.
. 6. 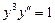 .
.
7. 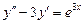 . 8.
. 8.  .
.
Вариант 17.
1. 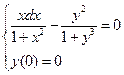 . 2.
. 2. 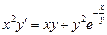 . 3.
. 3.  .
.
4. 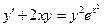 . 5.
. 5. 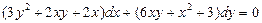 . 6.
. 6. 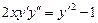 .
.
7. 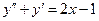 . 8.
. 8. 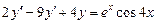 .
.
Вариант 18.
1. 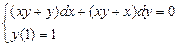 . 2.
. 2. 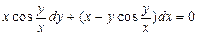 . 3.
. 3. 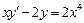 .
.
4. 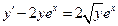 . 5.
. 5. 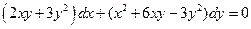 . 6.
. 6. 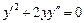 .
.
7. 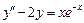 . 8.
. 8. 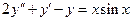 .
.
Вариант 19.
1. 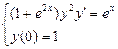 . 2.
. 2. 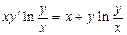 . 3.
. 3. 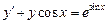 .
.
4. 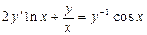 . 5.
. 5. 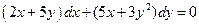 . 6.
. 6. 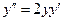 .
.
7. 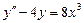 . 8.
. 8. 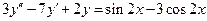 .
.
Вариант 20.
1. 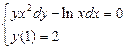 . 2.
. 2. 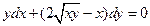 . 3.
. 3. 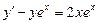 .
.
4. 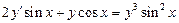 . 5.
. 5. 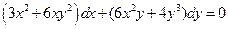 . 6.
. 6. 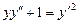 .
.
7. 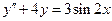 . 8.
. 8. 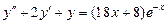 .
.
Вариант 21.
1. 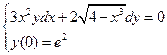 . 2.
. 2. 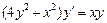 . 3.
. 3. 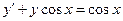 .
.
4. 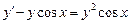 . 5.
. 5. 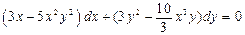 . 6.
. 6. 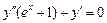 .
.
7. 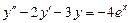 . 8.
. 8.  .
.
Вариант 22.
1. 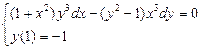 . 2.
. 2.  . 3.
. 3. 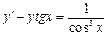 .
.
4. 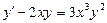 . 5.
. 5. 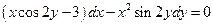 . 6.
. 6. 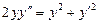 .
.
7. 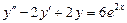 . 8.
. 8. 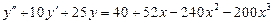 .
.
Вариант 23.
1. 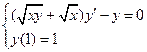 . 2.
. 2.  . 3.
. 3. 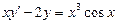 .
.
4. 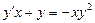 . 5.
. 5. 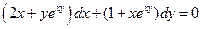 . 6.
. 6.  .
.
7. 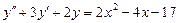 . 8.
. 8. 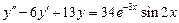 .
.
Вариант 24.
1. 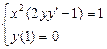 . 2.
. 2. 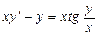 . 3.
. 3.  .
.
4. 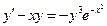 . 5.
. 5. 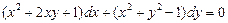 . 6.
. 6. 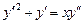 .
.
7. 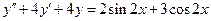 . 8.
. 8. 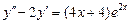 .
.
Вариант 25.
1. 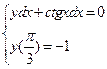 . 2.
. 2. 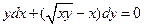 . 3.
. 3. 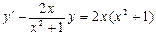 .
.
4. 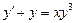 . 5.
. 5.  . 6.
. 6. 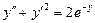 .
.
7. 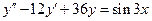 . 8.
. 8. 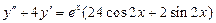 .
.
Вариант 26.
1. 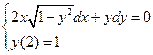 . 2.
. 2. 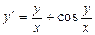 . 3.
. 3. 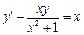 .
.
