Теорема существования и единственности решения задачи Коши.

Системы обыкновенных дифференциальных уравнений.

Нормальные системы.

Определение 1. Нормальная система обыкновенных дифференциальных уравнений имеет следующий вид:

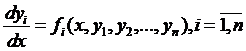(1.1)

где 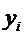, 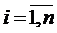– неизвестные функции от независимой переменной x, подлежащие определению; 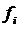, 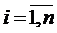– известные функции от 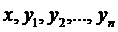, заданные и непрерывные в некоторой области. Число n называется порядком системы (1.1). В дальнейшем ограничимся рассмотрением систем второго порядка (n=2).

Определение 2. Пусть дана нормальная система уравнений

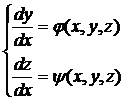(1.2)

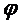где и 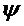– заданные и непрерывные в некоторой области функции. Пара функции (y(x); z(x)), определенная на (a,b), имеющая непрерывные производные и удовлетворяющая на (a,b) обоим уравнениям системы (1.2), называется ее решением.

Задача нахождения решения (y(x); z(x)), удовлетворяющего начальным условиям 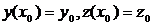, где 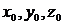– заданные числа (начальные данные), называется задачей Коши.

Теорема существования и единственности решения задачи Коши.

Пусть дана система уравнений (1.2) и пусть в некоторой области D (x,y,z) функци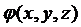и и 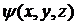непрерывны и имеют непрерывные частные производные по y, z. Пусть точка 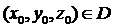. Тогда существует интервал (a,b) и определенные на нем непрерывно дифференцируемые функции y(x), z(x), удовлетворяющие системе (1.2) и начальным условиям 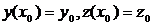, причем эти функции единственны.

Метод исключения.

Продифференцируем, например, первое уравнение системы уравнений (1.2) по независимой переменной x

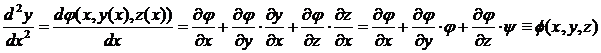
Вместо системы (1.2) запишем систему уравнений 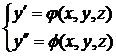(2.1)

(2.1)

Из первого уравнения системы (2.1) следует, что 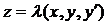. Подставим эту функцию во второе уравнение (2.1): 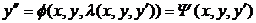. Итак, исключив из системы функцию z приходим к одному уравнению 2-го порядка, решая которое, получаем: 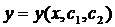. Теперь продифференцируем найденное выражение по x и подставим в функцию 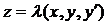. И тем самым получим 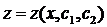. В результате получим решение в виде:

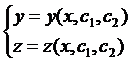(2.2)

Определение 1. Общим решением системы двух обыкновенных дифференциальных уравнений 1-го порядка является совокупность функций (2.2), непрерывно дифференцируемых на некотором интервале (a,b), которые при различных допустимых значениях произвольных постоянных удовлетворяют обоим уравнениям системы уравнений (1.2). При этом в области, в которой выполнены условия теоремы существования и единственности, можно получить решение любой задачи Коши.

Системы обыкновенных дифференциальных уравнений.

Нормальные системы.

Определение 1. Нормальная система обыкновенных дифференциальных уравнений имеет следующий вид:

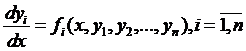(1.1)

где 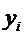, 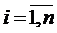– неизвестные функции от независимой переменной x, подлежащие определению; 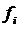, 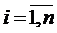– известные функции от 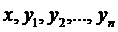, заданные и непрерывные в некоторой области. Число n называется порядком системы (1.1). В дальнейшем ограничимся рассмотрением систем второго порядка (n=2).

Определение 2. Пусть дана нормальная система уравнений

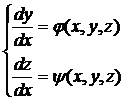(1.2)

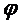где и 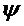– заданные и непрерывные в некоторой области функции. Пара функции (y(x); z(x)), определенная на (a,b), имеющая непрерывные производные и удовлетворяющая на (a,b) обоим уравнениям системы (1.2), называется ее решением.

Задача нахождения решения (y(x); z(x)), удовлетворяющего начальным условиям 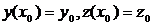, где 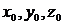– заданные числа (начальные данные), называется задачей Коши.

Теорема существования и единственности решения задачи Коши.

Пусть дана система уравнений (1.2) и пусть в некоторой области D (x,y,z) функци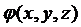и и 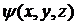непрерывны и имеют непрерывные частные производные по y, z. Пусть точка 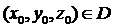. Тогда существует интервал (a,b) и определенные на нем непрерывно дифференцируемые функции y(x), z(x), удовлетворяющие системе (1.2) и начальным условиям 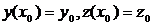, причем эти функции единственны.

Метод исключения.

Продифференцируем, например, первое уравнение системы уравнений (1.2) по независимой переменной x

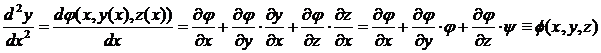
Вместо системы (1.2) запишем систему уравнений 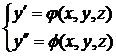(2.1)

(2.1)

Из первого уравнения системы (2.1) следует, что 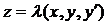. Подставим эту функцию во второе уравнение (2.1): 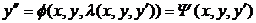. Итак, исключив из системы функцию z приходим к одному уравнению 2-го порядка, решая которое, получаем: 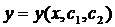. Теперь продифференцируем найденное выражение по x и подставим в функцию 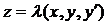. И тем самым получим 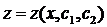. В результате получим решение в виде:

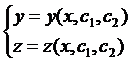(2.2)

Определение 1. Общим решением системы двух обыкновенных дифференциальных уравнений 1-го порядка является совокупность функций (2.2), непрерывно дифференцируемых на некотором интервале (a,b), которые при различных допустимых значениях произвольных постоянных удовлетворяют обоим уравнениям системы уравнений (1.2). При этом в области, в которой выполнены условия теоремы существования и единственности, можно получить решение любой задачи Коши.