Теорема о существовании и единственности решения Задачи Коши (3.2),(3.4). 4 страница
4. 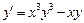 . 5.
. 5. 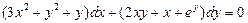 . 6.
. 6. 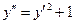 .
.
7. 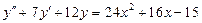 . 8.
. 8. 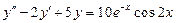 .
.
Вариант 27.
1. 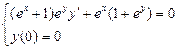 . 2.
. 2. 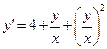 . 3.
. 3. 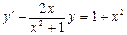 .
.
4. 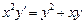 . 5.
. 5. 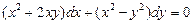 . 6.
. 6. 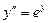 .
.
7. 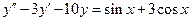 . 8.
. 8. 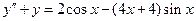 .
.
Вариант 28.
1. 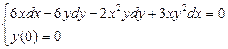 . 2.
. 2. 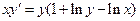 . 3.
. 3. 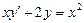 .
.
4. 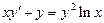 . 5.
. 5. 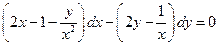 . 6.
. 6. 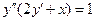 .
.
7. 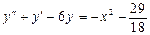 . 8.
. 8. 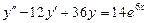 .
.
Вариант 29.
1. 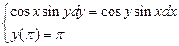 . 2.
. 2. 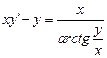 . 3.
. 3. 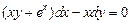 .
.
4. 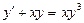 . 5.
. 5. 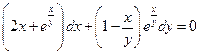 . 6.
. 6. 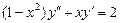 .
.
7. 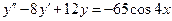 . 8.
. 8. 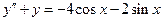 .
.
Вариант 30.
1. 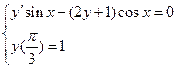 . 2.
. 2. 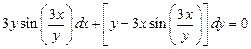 . 3.
. 3. 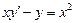 .
.
4. 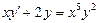 . 5.
. 5. 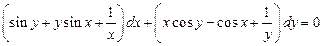 . 6.
. 6. 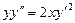 .
.
7. 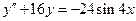 . 8.
. 8. 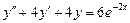 .
.
4. Ряды.
4.1. Числовые ряды.
Основные понятия и свойства
Числовым рядом называется сумма вида
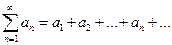 (4.1)
(4.1)
где 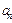 - числа, члены ряда.
- числа, члены ряда.
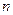 - ой частичной суммой ряда (4.1) называется сумма
- ой частичной суммой ряда (4.1) называется сумма 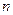 его первых членов
его первых членов
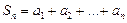 .
.
Рассмотрим последовательность частичных сумм:
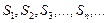 (4.2)
(4.2)
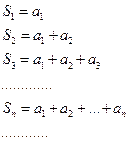
Если последовательность (4.2) имеет конечный предел 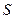 , т.е.
, т.е. 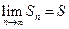 , то ряд (4.1) называется сходящимся,а число
, то ряд (4.1) называется сходящимся,а число 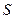 называют суммой ряда.
называют суммой ряда.
Если же последовательность (4.2) имеет бесконечный предел, или не имеет предела вообще, то ряд (4.1) называетсярасходящимся,ив этом случае этот ряд суммы не имеет.
Простейший пример ряда – сумма членов геометрической прогрессии:
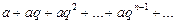 (4.3)
(4.3)
Здесь 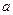 - первый член прогрессии,
- первый член прогрессии, 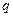 - ее знаменатель. По формуле суммы
- ее знаменатель. По формуле суммы 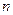 членов геометрической прогрессии
членов геометрической прогрессии 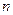 -ая частичная сумма ряда (4.3)
-ая частичная сумма ряда (4.3) 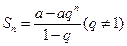 .
.
При вычислении предела последовательности частичных сумм ряда (4.3) рассматриваются три случая:
- если 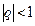 , то
, то 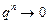 при
при 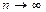 , поэтому
, поэтому 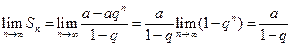 , т.е. в этом случае (бесконечно убывающей прогрессии) ряд (4.3) сходится и его сумма
, т.е. в этом случае (бесконечно убывающей прогрессии) ряд (4.3) сходится и его сумма 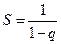 ;
;
- если 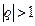 , то
, то 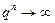 при
при 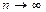 и
и 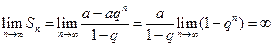 , таким образом, ряд (4.3) в этом случае расходится и суммы не имеет;
, таким образом, ряд (4.3) в этом случае расходится и суммы не имеет;
- если 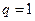 , то ряд (4.3) имеет вид:
, то ряд (4.3) имеет вид: 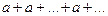 , а его
, а его 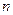 -ая частичная сумма
-ая частичная сумма 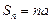
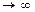 при
при 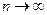 , т.е. ряд (4.3) в этом случае расходится и суммы не имеет;
, т.е. ряд (4.3) в этом случае расходится и суммы не имеет;
- если 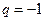 , то ряд (4.3) имеет вид:
, то ряд (4.3) имеет вид: 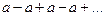 , поэтому при
, поэтому при 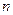 четном
четном  , а при
, а при 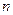 нечетном
нечетном 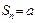 . А так как последовательность частичных сумм
. А так как последовательность частичных сумм 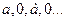 не имеет предела, то ряд в этом случае расходится и суммы не имеет.
не имеет предела, то ряд в этом случае расходится и суммы не имеет.
Вывод: бесконечно – убывающая геометрическая прогрессия ( 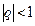 ) имеет сумму
) имеет сумму 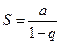 =
= 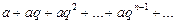 (4.4)
(4.4)
4.1). Исследовать на сходимость ряд 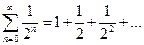 .
.
Этот ряд представляет собой сумму бесконечно – убывающей геометрической прогрессии с первым членом 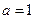 и знаменателем
и знаменателем 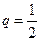 . Потому он сходится и его сумма
. Потому он сходится и его сумма 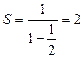 .
.
Свойства числовых рядов.
1. Если ряд 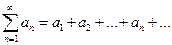 сходится, имеет сумму
сходится, имеет сумму 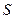 , то ряд
, то ряд 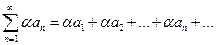 , где
, где 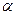 - заданное число, также сходится и его сумма равна
- заданное число, также сходится и его сумма равна 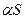 .
.
2. Если ряды 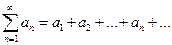 и
и 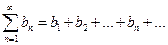 сходятся, имеют суммы
сходятся, имеют суммы 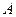 и
и 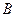 , то ряд
, то ряд 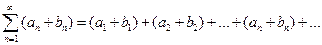 также сходится и имеет сумму
также сходится и имеет сумму 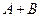 .
.
Аналогично, ряд 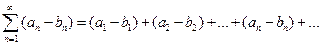 также сходится и имеет сумму
также сходится и имеет сумму 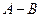 .
.
3. Если сходится ряд 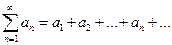 , то сходится и ряд
, то сходится и ряд 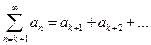 ,
,
полученный из данного отбрасыванием 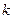 его первых членов. Верно и обратное.
его первых членов. Верно и обратное.
Необходимый признак сходимости и достаточный признак расходимости ряда.
Необходимый признак сходимости.Если ряд 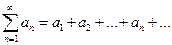 сходится, то его общий член
сходится, то его общий член 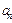 стремится к нулю при
стремится к нулю при 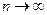 (
(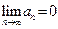 - необходимое условие сходимости).
- необходимое условие сходимости).
Доказательство. Поскольку ряд сходится, то последовательность его частичных сумм 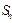 имеет конечные предел при
имеет конечные предел при  :
: 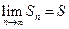 . При этом последовательность
. При этом последовательность 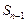 очевидно также сходится, и имеет тот же предел:
очевидно также сходится, и имеет тот же предел: 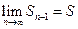 . А так как
. А так как 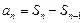 , то
, то 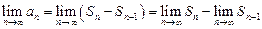
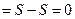 . Что и требовалось доказать.
. Что и требовалось доказать.
Достаточный признак расходимости.Если 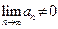 , т.е. общий член ряда не стремится к нулю при
, т.е. общий член ряда не стремится к нулю при 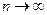 , то ряд расходится.
, то ряд расходится.
Доказательство от противного. Предположим, что ряд сходится, тогда по необходимому признаку его общий член стремится к нулю при 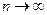 . Но это противоречит условию. Потому данный ряд расходится.
. Но это противоречит условию. Потому данный ряд расходится.
4.2). Исследовать на сходимость ряд 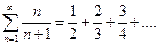 .
.
Проверим выполнение необходимого условия сходимости для этого ряда.
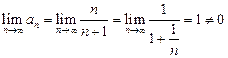 . Поэтому данный ряд расходится.
. Поэтому данный ряд расходится.
4.3). Исследовать на сходимость ряд 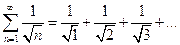 .
.
Необходимое условие сходимости для этого ряда выполнено: 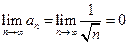 . Но, так как
. Но, так как
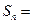
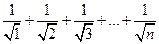
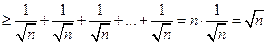 , т.е.
, т.е. 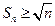 , то
, то 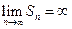 . Таким образом, данный ряд расходится. Этот пример показывает, что хотя признак
. Таким образом, данный ряд расходится. Этот пример показывает, что хотя признак 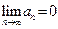 является необходимым, но он недостаточен для сходимости ряда.
является необходимым, но он недостаточен для сходимости ряда.
Достаточные признаки сходимости знакоположительных рядов.
Ряд
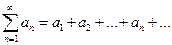 (4.5)
(4.5)
с положительными членами 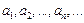 называется знакоположительным .
называется знакоположительным .
Последовательность частичных сумм такого ряда 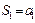 ,
, 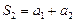 , …,
, …, 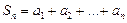 ,....
,....
является возрастающей последовательностью. А для такой последовательности имеются две возможности: 1. последовательность частичных сумм неограниченна, тогда 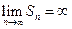 , т.е. ряд расходится; 2. последовательность частичных сумм ограничена,
, т.е. ряд расходится; 2. последовательность частичных сумм ограничена, 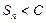 для
для 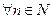 . Это означает, что существует конечный предел такой последовательности
. Это означает, что существует конечный предел такой последовательности 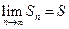 , т.е. ряд сходится. Перечислим несколько достаточных признаков сходимости знакоположительных рядов.
, т.е. ряд сходится. Перечислим несколько достаточных признаков сходимости знакоположительных рядов.
Даны два знакоположительных ряда
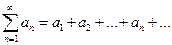 (4.6)
(4.6)
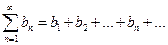 (4.7)
(4.7)
Первый признак сравнения.Если 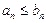 ,
, 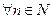 , то из сходимости ряда (4.7) следует сходимость ряда (4.6). А из расходимости ряда (4.6) следует расходимость ряда (4.7).
, то из сходимости ряда (4.7) следует сходимость ряда (4.6). А из расходимости ряда (4.6) следует расходимость ряда (4.7).
Второй признак сравнения.Если существует конечный предел 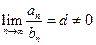 , то ряды (4.6) и (4.7) сходятся и расходятся одновременно.
, то ряды (4.6) и (4.7) сходятся и расходятся одновременно.
Признак Даламбера.Если для знакоположительного ряда (4.5) существует конечный или бесконечный предел 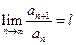 , то ряд (4.5) сходится при
, то ряд (4.5) сходится при 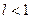 и расходится при
и расходится при 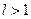 .
.
4.4). Исследовать на сходимость ряд 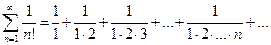
Вычислим предел отношения 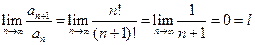 . Так как
. Так как 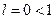 , то данный ряд сходится по признаку Даламбера.
, то данный ряд сходится по признаку Даламбера.
Радикальный признак сходимости.Еслидля знакоположительного ряда (4.5) существует конечный или бесконечный предел 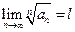 , то при
, то при 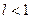 ряд сходится. А при
ряд сходится. А при 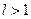 ряд расходится.
ряд расходится.
4.5). Исследовать на сходимость ряд 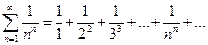 .
.
Следуя радикальному признаку сходимости вычислим предел 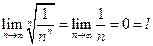 . Так как
. Так как
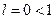 , то данный ряд сходится.
, то данный ряд сходится.
Интегральный признак сходимости Коши.Дан знакоположительный ряд (4.5), члены которого не возрастают, функция 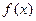 - непрерывная, невозрастающая и такая, что
- непрерывная, невозрастающая и такая, что 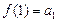 ,
,
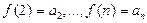 . Тогда ряд (4.5) и несобственный интеграл
. Тогда ряд (4.5) и несобственный интеграл 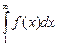 сходятся и расходятся одновременно.
сходятся и расходятся одновременно.
4.6). Исследовать на сходимость ряд 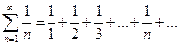 , называемый гармоническим.
, называемый гармоническим.
Для этого ряда выполнено необходимое условие сходимости: 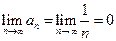 . Но, пользуясь интегральным признаком сходимости Коши, можем утверждать, что сходимость или расходимость этого ряда обусловлена сходимостью или расходимостью несобственного интеграла
. Но, пользуясь интегральным признаком сходимости Коши, можем утверждать, что сходимость или расходимость этого ряда обусловлена сходимостью или расходимостью несобственного интеграла 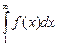 , где
, где 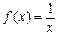 . Ранее, в примере 1.30), было показано, что несобственный интеграл
. Ранее, в примере 1.30), было показано, что несобственный интеграл 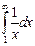 расходится. А это означает, что и данный гармонический ряд тоже расходится.
расходится. А это означает, что и данный гармонический ряд тоже расходится.
4.7). Исследовать на сходимость обобщенный гармонический ряд
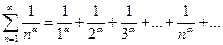 (4.8)
(4.8)
Следуя интегральному признаку сходимости Коши составим функцию 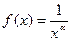 . В примере 1.31) было показано, что несобственный интеграл
. В примере 1.31) было показано, что несобственный интеграл 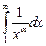 сходится при
сходится при 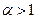 , а, значит, сходится и обобщенный гармонический ряд (4.8). При
, а, значит, сходится и обобщенный гармонический ряд (4.8). При 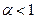 интеграл
интеграл 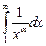 расходится, потому и ряд (4.8) тоже расходящийся.
расходится, потому и ряд (4.8) тоже расходящийся.
Теперь очевидно, что, например, ряд 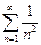 сходится как обобщенный гармонический при
сходится как обобщенный гармонический при 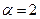 . А ряд
. А ряд 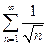 - расходится как обобщенный гармонический при
- расходится как обобщенный гармонический при 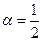 .
.
Знакопеременные ряды.
Ряд
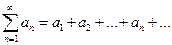 (4.9)
(4.9)
с членами разных знаков называется знакопеременным рядом.
Знакопеременный ряд (4.9) называется абсолютно сходящимся,если сходится ряд
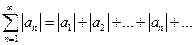 (4.10)
(4.10)
составленный из абсолютных значений его членов.
Знакопеременный сходящийся ряд (4.9) называется условно сходящимся, если ряд (4.10) расходится.
Всякий абсолютно сходящийся ряд является в то же время и сходящимся рядом.
Знакочередующийся– это ряд, знаки членов которого строго чередуются:
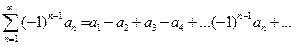 (4.11)
(4.11)
Здесь 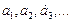 - положительные числа.
- положительные числа.
