Задачи Коши. Теорема существования и единственности решения
Задачи, приводящие к ду
Задача 1
Материальная точка массы m замедляет свое движение под действием силы сопротивления среды, пропорциональной квадрату скорости V. Найти зависимость скорости от времени. Найти скорость точки через 3 с после начала замедления, если V(0)=100 м/с, а V(l)=50 м/с.
Решение: Примем за независимую переменную время Т, отсчитываемое от начала замедления движения материальной точки. Тогда скорость точки V будет функцией Т, т. е. V=V(T). Для нахождения V(T) воспользуемся вторым законом Ньютона (основным законом механики): m • a=F, где а=V'(T) - есть ускорение движущегося тела, F - результирующая сила, действующая на тело в процессе движения.
В данном случае F=- KV2, К > 0 - коэффициент пропорционально-сти (знак минус указывает на то, что скорость тела уменьшается). Следовательно, функция V=V(T) является решением дифференциального уравнения 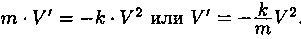 , Здесь m - масса тела.
, Здесь m - масса тела.
Как будет показано ниже (пример 2.5), 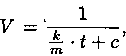 где с - const.
где с - const.
Найдя зависимость скорости от времени, легконайти скорость точки через 3 с после начала замедления.
Найдем сначала параметры k/m и с. Согласно условию задачи, имеем: 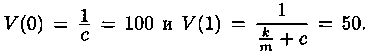 Отсюда
Отсюда 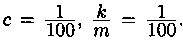
Следовательно, скорость точки изменяется по закону 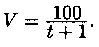 Поэтому V(3)=25 м/с.
Поэтому V(3)=25 м/с.
Задача 2
Найти кривую, проходящую через точку (4; 1), зная, что отрезок любой касательной к ней, заключенный между осями координат, делится в точке касания пополам.
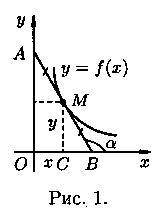 Решение: Пусть М(х; у) - произвольная точка кривой, уравнение которой y=ƒ(х). Для определенности предположим, что кривая расположена в первой четверти (см. рис.1).
Решение: Пусть М(х; у) - произвольная точка кривой, уравнение которой y=ƒ(х). Для определенности предположим, что кривая расположена в первой четверти (см. рис.1).
Для составления дифференциального уравнения воспользуемся геометрическим смыслом первой производной: tg а есть угловой коэффициент касательной; в точке М(х;υ) он равен y', т. е. y'=tg а.
Из рисунка видно, что 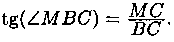 Но
Но 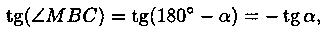
МС=υ. По условию задачи АМ=МВ, следовательно, ОС=СВ=х. Таким образом, получаем - tg a=у/x или y'=- у/x. Решением полученного дифференциального уравнения является функция y=4/x (гипербола). Решение будет приведено в п. 2.2 (пример 2.4).
Другие задачи
Можно показать, что:
• закон изменения массы радия в зависимости от времени («радиоактивный распад») описывается дифференциальным уравнением 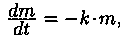 где К > 0 - коэффициент пропорциональности, м(Т) - масса радия в момент Т;
где К > 0 - коэффициент пропорциональности, м(Т) - масса радия в момент Т;
• «закон охлаждения тел», т. е. закон изменения температуры тела в зависимости от времени, описывается уравнением 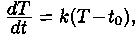 где T(t) - температура тела в момент времени t, k - коэффициент про-порциональности, tо - температура воздуха (среды охлаждения);
где T(t) - температура тела в момент времени t, k - коэффициент про-порциональности, tо - температура воздуха (среды охлаждения);
• зависимость массы х вещества, вступившего в химическую реакцию, от времени Т во многих случаях описывается уравнением 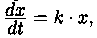 где К - коэффициент пропорциональности;
где К - коэффициент пропорциональности;
• «закон размножения бактерий» (зависимость массы м бактерий от времени Т) описывается уравнением m't=k•m, где k > 0;
• закон изменения давления воздуха в зависимости от высоты над уровнем моря описывается уравнением 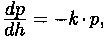 где р(Н) - атмосферное давление воздуха на высоте h, k > 0.
где р(Н) - атмосферное давление воздуха на высоте h, k > 0.
Уже приведенные примеры указывают на исключительно важную роль дифференциальных уравнений при решении самых разнообразных задач.
Основные понятия теории ду
Соотношение вида: 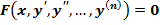 называется ДУ относительно функции y=y(x)
называется ДУ относительно функции y=y(x)
Порядком ДУ наз. порядок старшей производной входящей в это уравнение. Если искомая функция зависит от одной переменной то ДУ наз. обыкновенным, а если больше (2е или более), то уравнение наз. Уравнением частных производных.
Решением или интегралом ДУ наз. всякая функция y=f(x), которая превращает его в тождество.
Уравнение Бернулли
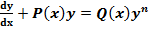
Здесь Р(х) и Q(x) непрерывная функция от х, а п≠0≠ 1
Это уравнение можно привести к линейному сдел преоброзованием разделив его на 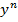
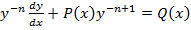
Делаем замену: z= 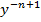
Получим 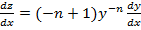
Подставим данное уравнение в 1е и получим:
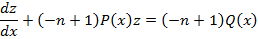
Получили линейное уравнение
Особые решения ду 1 порядка
Особые точки и особые решения уравнения первого порядка. Если в окрестности точки (x0, y0) плоскости для уравнения 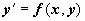 выполняются условия существования и единственности решения задачи Коши (непрерывность f(x, y) и
выполняются условия существования и единственности решения задачи Коши (непрерывность f(x, y) и 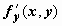 ), то через эту точку проходит единственная интегральная кривая. Если эти условия нарушаются, точку (x0, y0) называют особой точкой дифференциального уравнения. Через особую точку может не проходить ни одной
), то через эту точку проходит единственная интегральная кривая. Если эти условия нарушаются, точку (x0, y0) называют особой точкой дифференциального уравнения. Через особую точку может не проходить ни одной 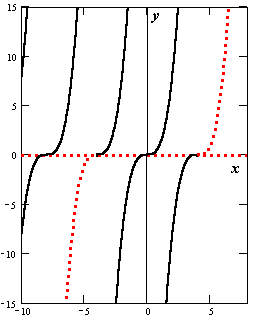 интегральной кривой (т.е. задача
интегральной кривой (т.е. задача 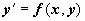 , y(x0) = y0 не имеет решения); может проходить одна интегральная кривая; может проходить несколько интегральных кривых. Особые точки могут образовать кривую, которая сама является интегральной кривой уравнения. Решение уравнения, в каждой точке которого нарушается его единственность, называют особым решением. Для примера рассмотрим уравнение
, y(x0) = y0 не имеет решения); может проходить одна интегральная кривая; может проходить несколько интегральных кривых. Особые точки могут образовать кривую, которая сама является интегральной кривой уравнения. Решение уравнения, в каждой точке которого нарушается его единственность, называют особым решением. Для примера рассмотрим уравнение 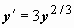 . Здесь
. Здесь 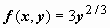 - непрерывна в любой точке (x, y), но
- непрерывна в любой точке (x, y), но 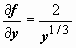 - не имеет конечного предела при
- не имеет конечного предела при 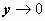 , т.е. в любой точке (x, y) при y = 0 нарушается условие существования непрерывной производной
, т.е. в любой точке (x, y) при y = 0 нарушается условие существования непрерывной производной 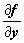 . Следовательно, любая точка (x, 0) является особой точкой уравнения. Прямая y = 0, очевидно, интегральная кривая уравнения (функция y = 0 удовлетворяет уравнению). Найдём общее решение этого уравнения:
. Следовательно, любая точка (x, 0) является особой точкой уравнения. Прямая y = 0, очевидно, интегральная кривая уравнения (функция y = 0 удовлетворяет уравнению). Найдём общее решение этого уравнения: 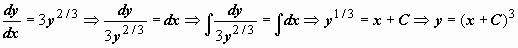 . Несколько таких функций приведено на рисунке справа вверху вместе с решением y = 0. В любой точке (x, 0) нарушается единственность решения, таким образом, решение y = 0 - особое. На самом деле через любую точку (x, 0)проходит бесконечное количество интегральных кривых, так как любая кривая, составленная из частей особого и неособых решений (одна такая кривая выделена красным пунктиром), также является интегральной кривой.
. Несколько таких функций приведено на рисунке справа вверху вместе с решением y = 0. В любой точке (x, 0) нарушается единственность решения, таким образом, решение y = 0 - особое. На самом деле через любую точку (x, 0)проходит бесконечное количество интегральных кривых, так как любая кривая, составленная из частей особого и неособых решений (одна такая кривая выделена красным пунктиром), также является интегральной кривой.
Формула Лиувиля
Теорема 14.5.6.1. Определитель Вронского системы y1(x), y2(x), …, yn(x) решений однородного уравнения удовлетворяет уравнению 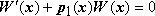 где p1(x) - коэффициент при n - 1 производной.
где p1(x) - коэффициент при n - 1 производной.
Док-во. Докажем эту теорему для уравнения второго порядка 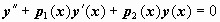 Пусть y1(x), y2(x) - частные решения этого уравнения, тогда ,
Пусть y1(x), y2(x) - частные решения этого уравнения, тогда , 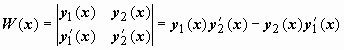 .
. 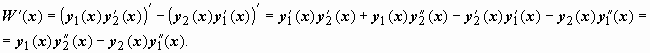 Так как y1(x), y2(x) - решения уравнения, то ,
Так как y1(x), y2(x) - решения уравнения, то , 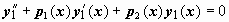
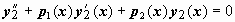 . Умножим первое из этих уравнений на - y2(x), второе - на y1(x) и сложим:
. Умножим первое из этих уравнений на - y2(x), второе - на y1(x) и сложим: 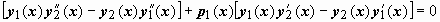
В первой из квадратных скобок стоит W(x), во второй - , поэтому 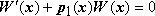 , что и требовалось доказать.
, что и требовалось доказать.
Для доказательства этой теоремы в общей случае надо знать правило дифференцирования функциональных определителей: производная определителя n-го порядка равна сумме n определителей, которые получаются из исходного определителя построчным дифференцированием. Для определителя Вронского 
так как первые n - 1 определитель содержат равные строки и равны нулю. Каждая из функций y1(x), y2(x), …, yn(x) удовлетворяет уравнению 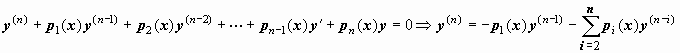 поэтому, поставив эти выражения в последнюю строку и пользуясь свойствами определителей, получим
поэтому, поставив эти выражения в последнюю строку и пользуясь свойствами определителей, получим 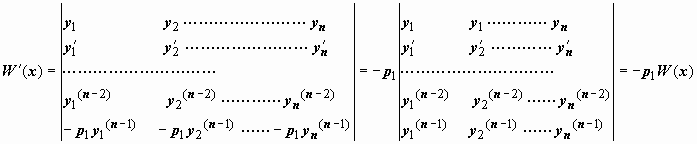
т.е. 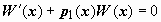 .
.
Решим это уравнение относительно W(x). Функция W(x) = 0 является решением этого уравнения; если 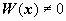 то
то 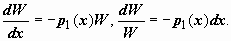 Интегрируем последнее выражение в пределах от x0 до x:
Интегрируем последнее выражение в пределах от x0 до x: 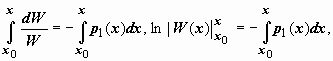
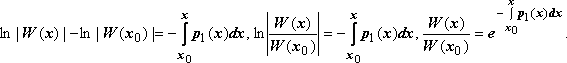 (Мы отбросили знак модуля у дроби, так как W(x) - непрерывная функция, не обращающаяся в нуль, поэтому значения W(x) и W(x0) всегда имеют один знак). Окончательно .
(Мы отбросили знак модуля у дроби, так как W(x) - непрерывная функция, не обращающаяся в нуль, поэтому значения W(x) и W(x0) всегда имеют один знак). Окончательно . 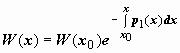 (28)
(28)
Формула (28)называется формулой Лиувилля. Из неё также следуют результаты предыдущих разделов: если W(x0) = 0, то 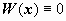 ; если
; если 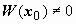 , то
, то 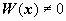 ни в одной точке интервала (a, b).
ни в одной точке интервала (a, b).
Интегрирование систем ДУ
Системы дифференциальных уравнений n–го порядка можно решать сведением к уравнению n–го порядка. Такой метод решения систем называетсяметодом исключения.
Рассмотрим, например, нормальную систему дифференциальных уравнений 2 –го порядка
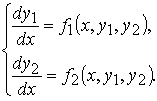
Исключим функцию y2. Для этого сначала выразим y2 через x и y1 из первого уравнения системы , затем продифференцируем по x первое уравнение системы, заменяя y2 полученным для него выражением, а производную y2 − правой частью второго уравнения системы:
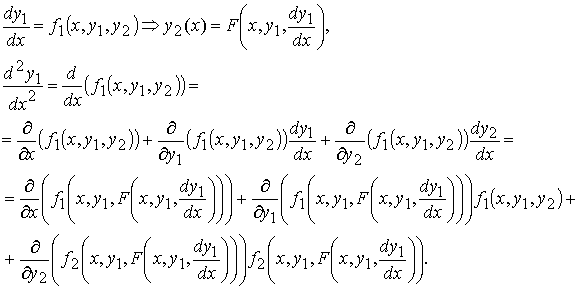
Получили обыкновенное дифференциальное уравнение 2 –го порядка
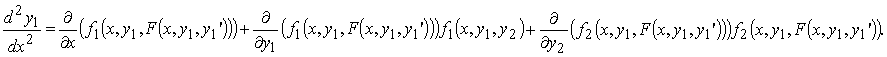
Таким же образом решают методом исключения произвольные системы n–го порядка: дифференцируют уравнения системы и, последовательно исключая функции y2, ..., yn и их производные, сводят систему к одному дифференциальному уравнению n–го порядка относительно y1.
Типы точек покоя
Пусть имеем систему двух линейных однородных дифференциальных уравнений с постоянными коэффициентами причем
(1)
Причём
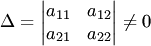
Точка 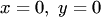 , в которой правые части уравнений системы (1) обращаются в ноль, называется точкой покоя системы (1).
, в которой правые части уравнений системы (1) обращаются в ноль, называется точкой покоя системы (1).
Для исследования точки покоя системы (1) надо составить характеристическое уравнение
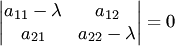 (2)
(2)
и найти его корни 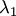 и
и 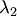 .
.
Возможны следующие случаи.
1. Корни 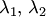 характеристического уравнения (2) вещественные и разные:
характеристического уравнения (2) вещественные и разные:
а) 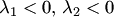 . Точка покоя асимптотически устойчива (устойчивый узел, рис. 32);
. Точка покоя асимптотически устойчива (устойчивый узел, рис. 32);
б) 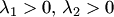 . Точка покоя неустойчива (неустойчивый узел, рис. 33);
. Точка покоя неустойчива (неустойчивый узел, рис. 33);
в) 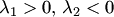 . Точка покоя неустойчива (седло, рис. 34).
. Точка покоя неустойчива (седло, рис. 34).
2. Корни характеристического уравнения (2) комплексные: 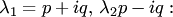
а) 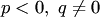 . Точка покоя асимптотически устойчива (устойчивый фокус, рис.35);
. Точка покоя асимптотически устойчива (устойчивый фокус, рис.35);
б) 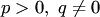 . Точка покоя неустойчива (неустойчивый фокус, рис.36);
. Точка покоя неустойчива (неустойчивый фокус, рис.36);
в) 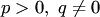 . Точка покоя устойчива (центр, рис. 37).
. Точка покоя устойчива (центр, рис. 37).
3. Корни 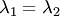 кратные:
кратные:
а) 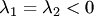 . Точка покоя асимптотически устойчива (устойчивый узел, рис.38, 39);
. Точка покоя асимптотически устойчива (устойчивый узел, рис.38, 39);
б) 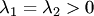 . Точка покоя неустойчива (неустойчивый узел, рис.40, 41).
. Точка покоя неустойчива (неустойчивый узел, рис.40, 41).
Теорема. Если все корни характеристического уравнения для системы (6) имеют отрицательную вещественную часть, то точка покоя системы (6) 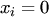
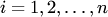 , асимптотически устойчива. Если хотя бы один корень характеристического уравнения имеет положительную вещественную часть, то точка покоя неустойчива.
, асимптотически устойчива. Если хотя бы один корень характеристического уравнения имеет положительную вещественную часть, то точка покоя неустойчива.
Числовой ряд сумма ряда
ЧИСЛОВОЙ РЯД – бесконечная сумма членов бесконечной числовой последовательности {an} называется числовым рядом:
a1 + a2+ a3 + … + an+ … = 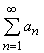 .
.
Каждому натуральному n сопоставляется сумма первых n членов последовательности {an}
S1 = a1, S2= a1 + a2, …, Sn = 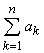 = a1 + a2 + a3 + … + an, …
= a1 + a2 + a3 + … + an, …
Значения Sn называют частичными суммами ряда. Они образуют последовательность {Sn} последовательность частичных сумм (бесконечного) ряда an – общий член ряда.
Если последовательность частичных сумм данного ряда имеет предел S,то есть
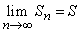 ,
,
то ряд сходится и S – его сумма. Записывается это следующим образом:
a1 + a2 + a3 + … + an + … = S, или 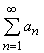 = S.
= S.
В противном случае ряд называют расходящимся.
Таким образом, сумма ряда – это, по определению, предел последовательности его частичных сумм.
Пусть есть геометрическая прогрессия bn = b1qn–1, знаменатель которой qпо абсолютной величине меньше единицы (–1 < q < 1). Вычислим сумму первых n членов геометрической прогрессии:
Sn= b1+ b1qn + b1q2 + …+ b1qn–1= 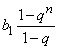 .
.
Очевидно, что при |q| < 1 с ростом n значение qn стремится к нулю. Тогда значение Sn стремится к 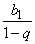 и это число называется суммой всех членов бесконечной убывающей геометрической прогрессии: b1 + b1qn + b1q2 + …=
и это число называется суммой всех членов бесконечной убывающей геометрической прогрессии: b1 + b1qn + b1q2 + …= 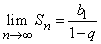 .
.
Знакочередующиеся ряды
Переходя к рассмотрению рядов, члены которых уже не обязательно положительны, остановимся сначала на одном важном частном типе этих рядов - на рядах знакочередующихся, теория которых сравнительно проста.
Ряд называется знакочередующимся, если любые два его соседних члена суть числа разных знаков.
Несколько изменяя употреблявшуюся выше символику, будем обозначать через an не сам общий член ряда, а его абсолютную величину. Тогда, предполагая для определенности, что первый член знакочередующегося ряда положителен, мы сможем записать этот ряд в форме*
a1 - a2 + a3 - a4 + a5 - ... (36)
Теорема Лейбница. Если абсолютная величина общего члена знакочередующегося ряда убывает и стремится к нулю, то этот ряд сходится.
Действительно, допустим, что ряд (36) таков, что
a1 > a2 > a3 > a4 > ..., (37)
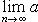
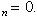 (38)
(38)
Образуем частичные суммы S2n:
S2 = (a1 - a2),
S4 = (a1 - a2) + (a3 - a4),
S6 = (a1 - a2) + (a3 - a4) + (a5 - a6),
. . . . . . . . . . . . . .
Благодаря (37), все скобки положительны. Значит,
S2 < S4 < S6 < ...
Иначе говоря, последовательность {S2n} возрастает. С другой стороны,
S2n = a1 - (a2 - a3) - (a4 - a5) - ... - (a2n-2 - a2n-1) - a2n,
откуда ясно, что
S2n < a1.
Как известно, при этих условиях существует конечный предел
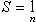
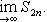
Но
S2n+1 = S2n + a2n+1,
откуда в связи с (38) вытекает, что сумма S2n+1 с возрастанием n также стремится к S. Итак, при достаточно больших n сумма Sn будет сколь угодно близка к Sнезависимо от четности n. Иначе говоря,
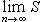
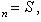
чем и доказана теорема.
Заметим, что теорема перестает быть верной, если отбросить условие убывания an. Например, знакочередующийся ряд
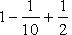
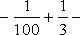
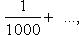
как легко видеть, расходится
Мажорируемый ряд.
Ряды Тейлора и Маклорена.
Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:
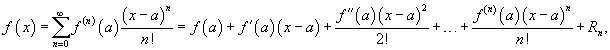
где Rn − остаточный член в форме Лагранжа определяется выражением
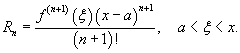
Если приведенное разложение сходится в некотором интервале x, т.е. 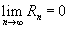 , то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.
, то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.
Если a = 0, то такое разложение называется рядом Маклорена:
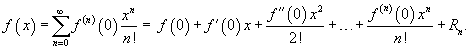
43.
44.
Четные и нечетные функции
Разложение в ряд Фурье четной функции, определенной в интервале [− L, L], имеет вид
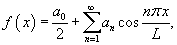
где
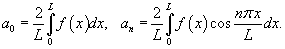
Разложение в ряд Фурье нечетной функции, заданной в интервале [− L, L], выражается формулой
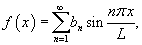
где коэффициенты Фурье равны
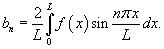
Интеграл Фурье
Достаточные условия представимости функции в интеграл Фурье.
Для того, чтобы f(x) была представлена интегралом Фурье во всех точках непрерывности и правильных точках разрыва, достаточно:
1) абсолютной интегрируемости на 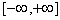
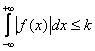 (т.е. интеграл сходится)
(т.е. интеграл сходится)
2) на любом конечном отрезке [-L, L] функция была бы кусочно-гладкой
3) в точках разрыва функции, ее интеграл Фурье определяется полусуммой левого и правого пределов в этих точках, а в точках непрерывности к самой функции f(x)
Интегралом Фурье функции f(x) называется интеграл вида:
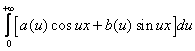
, где 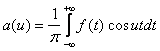 ,
,
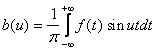 .
.
Интеграл Фурье для четной и нечетной функции
Пусть f(x)-четная функция, удовлетворяющая условиям представимости интегралом Фурье.
Учитывая, что 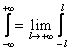 , а также свойство интегралов по симметричному относительно точки x=0 интервалу от четных функций, из равенства (2) получаем:
, а также свойство интегралов по симметричному относительно точки x=0 интервалу от четных функций, из равенства (2) получаем:
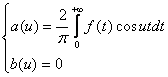 (3)
(3)
Таким образом, интеграл Фурье четной функции f(x) запишется так:
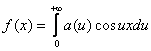 ,
,
где a(u) определяется равенством (3).
Рассуждая аналогично, получим, для нечетной функции f(x) :
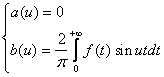 (4)
(4)
и, следовательно, интеграл Фурье нечетной функции имеет вид:
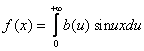 ,
,
где b(u) определяется равенством (4).
Комплексная форма интеграла Фурье
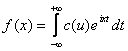 , (5)
, (5)
где
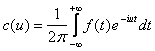 .
.
Выражение в форме (5) является комплексной формой интеграла Фурье для функции f(x).
Если в формуле (5) заменить c(u) его выражением, то получим:
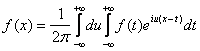 , где правая часть формулы называется двойным интегралом
, где правая часть формулы называется двойным интегралом
Фуpье в комплексной форме. Переход от интеграла Фурье в комплексной форме к интегралу
в действительной форме и обратно осуществим с помощью формул:
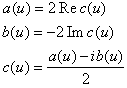
Формулы дискретного преобразования Фурье
Обратное преобразование Фурье.
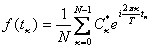
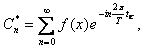
где n=1,2,..., k=1,2,...
Дискретным преобразованием Фурье - называется N-мерный вектор 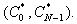
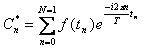
при этом, 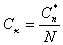 .
.
50. Преобразование Фурье
Дискретное преобразование Фурье трансформирует последовательность комплексных (либо вещественных) чисел xn в последовательность комплексных чисел Xn . Прямое и обратное преобразования Фурье определяются, как:
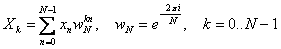
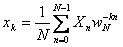
Приведенные выше формулы имеют сложность O(N 2), однако широко известен способ снизить сложность дискретного преобразования Фурье доO(N·log(N)). Быстрое преобразование Фурье широко используется как само по себе, так и для ускорения вычисления других преобразований - быстрого вычисления свертки и кросс-корреляции.
Условие Коши-Римана
Теорема (необходимые условия дифференцирования). Пусть функция 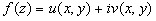 дифференцируема в точке
дифференцируема в точке 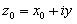 . Тогда функции
. Тогда функции 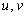 имеют частные производные в точке
имеют частные производные в точке 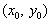 удовлетворяют следующим условиям:
удовлетворяют следующим условиям:
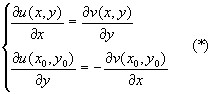
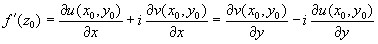 .
.
Условия (*) называются условиями Коши-Римана.
Доказательство.
Пусть 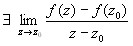 . Какую бы не выбрали траекторию
. Какую бы не выбрали траекторию 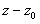 отношение
отношение 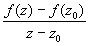 будет стремится к одному и тому же числу.
будет стремится к одному и тому же числу.
Выберем 2 траектории.
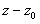
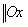 (действительная ось)
(действительная ось)
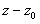
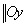 (мнимая ось)
(мнимая ось)
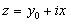
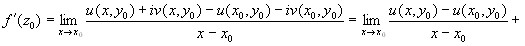
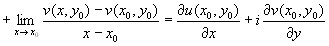 .
.
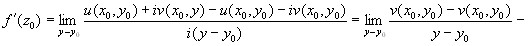
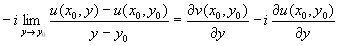 .
.
Сравнивая вещественные и мнимые части первого и второго уравнения получаем условие Коши-Римана.
Пример.
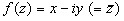
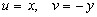
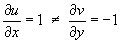
Конформные отображения
Взаимно однозначное отображение области D на область D* (евклидова пространства или риманова многообразия) называется конформным (лат. conformis — подобный), если в окрестности любой точки D дифференциал этого преобразования есть композиция ортогонального преобразования и гомотетии.
Этот термин пришёл из комплексного анализа, изначально использовался только для конформных отображений областей плоскости.
Связанные определения
Если при конформном отображении сохраняется ориентация, то говорят о конформном отображении первого рода; если же она меняется на противоположную, то говорят о конформном отображении второго рода либо антиконформном отображении .
Две метрики 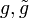 на гладком многообразии M называются конформноэквивалентными если существует гладкая функция
на гладком многообразии M называются конформноэквивалентными если существует гладкая функция 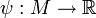 такая что
такая что 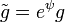 . В этом случае тождественное отображение на M индуцирует конформное отображение
. В этом случае тождественное отображение на M индуцирует конформное отображение 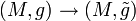 .
.
Свойства
Конформное отображение сохраняет форму бесконечно малых фигур;
Конформное отображение сохраняет углы между кривыми в точках их пересечения (свойство сохранения углов).
Это свойство можно также взять за определение конформного отображения.
Теорема Лиувилля: Всякое конформное отображение области евклидова пространства 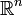 при
при 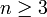 можно представить в виде конечного числа суперпозиций — изометрий и инверсий.
можно представить в виде конечного числа суперпозиций — изометрий и инверсий.
Кривизна Вейля сохраняется при конформном отображении, то есть если 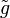 и g — конформноэквивалентные метрические тензоры, то
и g — конформноэквивалентные метрические тензоры, то
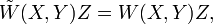
где 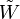 и W обозначают тензоры Вейля для
и W обозначают тензоры Вейля для 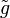 и g соответственно.
и g соответственно.
Для конформно-эквивалентых метрик 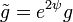
Связности связаны следующей формулой:
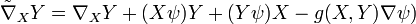
Кривизны связаны следующей формулой:
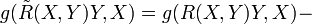
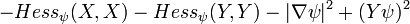
если g(X,X) = g(Y,Y) = 1,g(X,Y) = 0,Xψ = 0 а Hessψ обозначает Гессиан функции ψ.
Формулу для секционных кривизн можно записать в следующем виде:
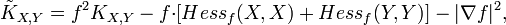
где f = e − ψ.
При вычислении скалярной кривизны n-мерного риманова многообразия, удобнее записывать конформный фактор в виде 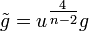 . В этом случае:
. В этом случае:
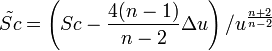
Теорема Коши. Интеграл Коши
Результат, полученный в примере 3-5, является частным случаем теоремы Коши и, если 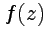 является аналитической (или только дифференцируемой) функцией в области
является аналитической (или только дифференцируемой) функцией в области 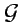 комплексной плоскости, то интеграл по любой замкнутой кривой
комплексной плоскости, то интеграл по любой замкнутой кривой  от
от 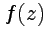 равен нулю:
равен нулю:
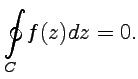 | (48) |
Теорема Коши имеет несколько важных следствий:
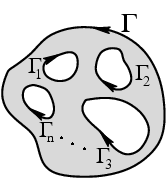 |  интеграл от интеграл от 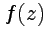 не зависит от пути интегрирования, а определяется только значениями начальной и конечной точек (см. пример 3-5 для аналитической функции не зависит от пути интегрирования, а определяется только значениями начальной и конечной точек (см. пример 3-5 для аналитической функции 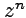 ); );  если если 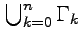 - объединенная граница многосвязной области (рис.17), то имеет место формула - объединенная граница многосвязной области (рис.17), то имеет место формула | ||
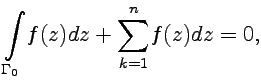 | (49) | ||
| Рис.17 | |||
где все участки границы обходятся в положительном направлении, т. е. когда захватываемая область остается слева при движении вдоль каждой кривой 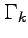 ;
;
 значение интеграла
значение интеграла 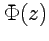 от функции
от функции 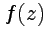 по некоторой кривой, соединяющей точки
по некоторой кривой, соединяющей точки 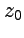 и
и 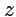 , т. е.:
, т. е.:
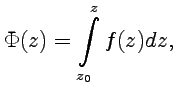 | (50) |
будет аналитической функцией переменной 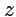 , причем
, причем 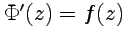 . Функция
. Функция 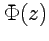 (50) называется первообразной, и для нее имеет место комплексный аналог формулы Ньютона-Лейбница:
(50) называется первообразной, и для нее имеет место комплексный аналог формулы Ньютона-Лейбница:
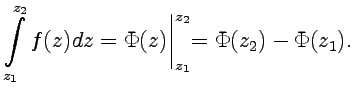 | (51) |
Ряд Лорана
Ряд Лорана. Пусть функция f(z) аналитична в кольце ρ ≤ |z − z0| ≤ R. Тогда для любой точки этого кольца 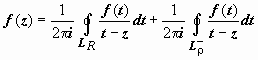 ; при этом окружности проходятся так, что область остаётся слева (следствие 3 раздела 19.7.2. Интегральная формула Коши). Изменим в интеграле по внутренней окружности направление обхода на противоположное:
; при этом окружности проходятся так, что область остаётся слева (следствие 3 раздела 19.7.2. Интегральная формула Коши). Изменим в интеграле по внутренней окружности направление обхода на противоположное: 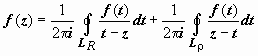 . Интеграл по внешней окружности преобразуем так, как и при выводе формулы Тейлора:
. Интеграл по внешней окружности преобразуем так, как и при выводе формулы Тейлора: 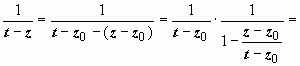 (так как | z – z0| < | t – z0| , то
(так как | z – z0| < | t – z0| , то 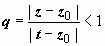 )
) 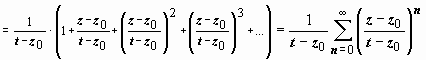 , и ряд сходится абсолютно, поэтому его можно почленно интегрировать:
, и ряд сходится абсолютно, поэтому его можно почленно интегрировать: 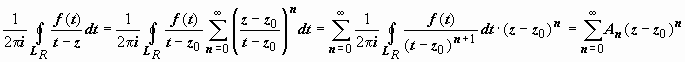 , где
, где 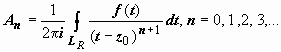 . Интеграл по внутренней окружности преобразуем аналогично, учитывая только, что на Lρ | t – z0| < | z – z0| :
. Интеграл по внутренней окружности преобразуем аналогично, учитывая только, что на Lρ | t – z0| < | z – z0| : 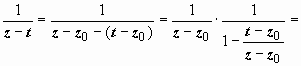
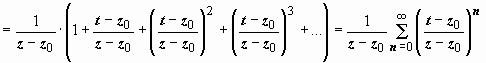 . И здесь ряд сходится абсолютно, поэтому его можно почленно интегрировать:
. И здесь ряд сходится абсолютно, поэтому его можно почленно интегрировать: 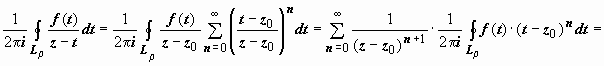
 ,
, 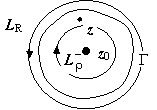 где
где 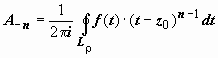 . Переобозначим n → −n, тогда форма коэффициентов ряда для Lρ совпадёт с формой коэффициентов ряда для LR:
. Переобозначим n → −n, тогда форма коэффициентов ряда для Lρ совпадёт с формой коэффициентов ряда для LR: 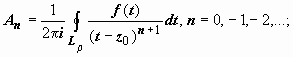 поэтому окончательно для интеграла по Lρ получим
поэтому окончательно для интеграла по Lρ получим 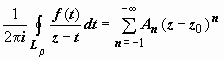 . Докажем, что и контур для вычисления коэффициентов может быть взят один и тот же. Действительно, пусть Γ - кусочно-гладкий контур, расположенный в кольце ρ ≤ |z − z0| ≤ R, и точка z0 расположена внутри этого контура. По теореме Коши для многосвязной области
. Докажем, что и контур для вычисления коэффициентов может быть взят один и тот же. Действительно, пусть Γ - кусочно-гладкий контур, расположенный в кольце ρ ≤ |z − z0| ≤ R, и точка z0 расположена внутри этого контура. По теореме Коши для многосвязной области 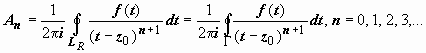 ;
; 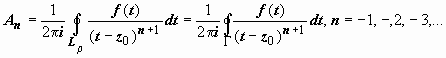 , поэтому для любого n
, поэтому для любого n 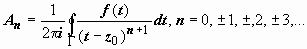 , и
, и
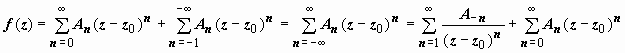 .
.
Этот ряд (содержащий и положительные, и отрицательные степени (z – z0), называется рядом Лорана функции f(z). Его часть, содержащая неотрицательные степени ( 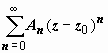 ), называется правильной; часть, содержащая отрицательные степени (
), называется правильной; часть, содержащая отрицательные степени ( 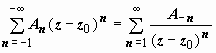 ), называется главной. Правильная часть, по самому своему построению, сходится в круге | z – z0| ≤ R, главная - во внешности круга | z – z0| ≥ ρ, поэтому весь ряд сходится в пересечении этих областей, т.е. в кольце ρ ≤ | z – z0| ≤ R. Так же, как и для ряда Тейлора, разложение в ряд Лорана единственно.
), называется главной. Правильная часть, по самому своему построению, сходится в круге | z – z0| ≤ R, главная - во внешности круга | z – z0| ≥ ρ, поэтому весь ряд сходится в пересечении этих областей, т.е. в кольце ρ ≤ | z – z0| ≤ R. Так же, как и для ряда Тейлора, разложение в ряд Лорана единственно.
Еще раз подчеркнем, что в ряд Лорана раскладывается функция, аналитическая в кольце, и ширина этого кольца определяется областью аналитичности функции, т.е. разложение теряет смысл там, где функция теряет аналитичность. Рассмотрим
Вычисление вычетов
Вычеты и их применение
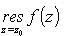 - вычет функции f(z) относительно изолированной особой точки z0:
- вычет функции f(z) относительно изолированной особой точки z0:
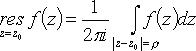
(в круге 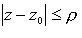 нет других особых точек).
нет других особых точек).
Если 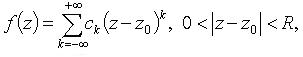 то
то
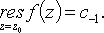
Вычисление вычетов
1. z0 - устранимая особая точка:
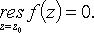
2. z0 - полюс:
а) z0 - простой полюс:
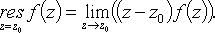
В частности, если 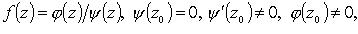 то
то
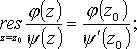
б) z0 - полюс порядка m:
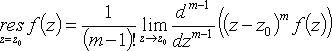
(формула также верна, если z0 - полюс порядка не выше m).
3. z0 - существенно особая точка. Вычет находится по разложению в ряд Лорана.
Основная теорема о вычетах
Основная теорема о вычетах
Если f(z) - аналитическая на границе 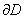 области D и внутри области, за исключением конечного числа особых точек z1, z2, ..., zn, лежащих в D, то
области D и внутри области, за исключением конечного числа особых точек z1, z2, ..., zn, лежащих в D, то
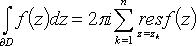
(обход контура положительный).
Вычисление интегралов от функций действительной переменной
1. 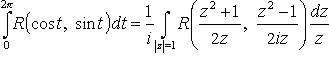 (R - рациональная функция двух переменных).
(R - рациональная функция двух переменных).
2. Если R(x) - рациональная функция, а 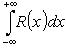 сходится, то
сходится, то
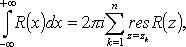
где zk - все особые точки функции R(z), лежащие в верхней полуплоскости (Im zk > 0).
Если 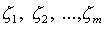 - особые точки функции R(z), лежащие в нижней полуплоскости, то
- особые точки функции R(z), лежащие в нижней полуплоскости, то
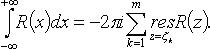
3. Если R(x) - рациональная функция, не обращающаяся в нуль на действительной оси, 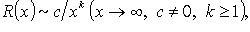 то
то
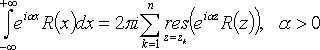
(zk - все особые точки, лежащие в верхней полуплоскости);
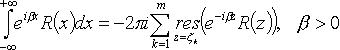
( 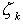 - все особые точки, лежащие в нижней полуплоскости).
- все особые точки, лежащие в нижней полуплоскости).
Замечание.
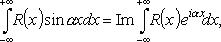
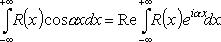
Теорема о свертке
Определение. Сверткой функций f1(t) и f2(t) называется функция 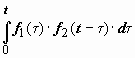 .
.
Свёртка обозначается символом f1 * f2: 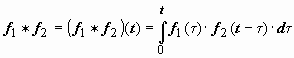 . Если f1(t) и f2(t) - функции-оригиналы, то их свёртка - тоже функция-оригинал, показатель роста которой превышает наибольший из показателей роста функций f1(t) и f2(t) не больше, чем на 1. Действительно, пусть
. Если f1(t) и f2(t) - функции-оригиналы, то их свёртка - тоже функция-оригинал, показатель роста которой превышает наибольший из показателей роста функций f1(t) и f2(t) не больше, чем на 1. Действительно, пусть 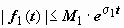 ,
, 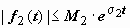 ,
, 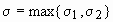 , тогда
, тогда 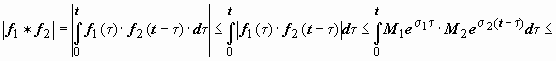
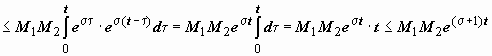 , так как t < e t.
, так как t < e t.
Свёртка функций коммутативна: f (t) * g (t) = g (t) * f (t), в этом легко убедиться, заменив в интеграле 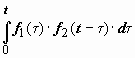 переменную τ на τ1 = t −τ.
переменную τ на τ1 = t −τ.
Можно показать, что свёртка обладает свой
