Теорема 1.1 (теорема Коши о существовании и единственности решения)
Если в уравнении 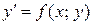 функция
функция 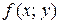 и ее частная производная
и ее частная производная 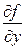 непрерывны в некоторой области
непрерывны в некоторой области 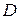 на плоскости
на плоскости 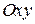 , содержащей некоторую точку
, содержащей некоторую точку 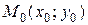 , то существует единственное решение этого уравнения
, то существует единственное решение этого уравнения 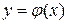 , удовлетворяющее условию
, удовлетворяющее условию 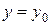 при
при 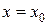 .
.
Геометрический смысл теоремы заключается в том, что существует и притом единственная функция 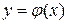 , график которой проходит через точку
, график которой проходит через точку 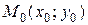 .
.
Из только что сформулированной теоремы вытекает, что уравнение 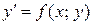 имеет бесчисленное множество решений.
имеет бесчисленное множество решений.
Каково бы ни было начальное условие 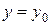 при
при 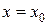 , можно найти такое значение
, можно найти такое значение 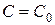 , что функция
, что функция 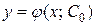 удовлетворяет данному начальному условию. При этом предполагается, что значения
удовлетворяет данному начальному условию. При этом предполагается, что значения 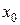 и
и 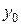 принадлежат к той области изменения переменных
принадлежат к той области изменения переменных 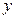 и
и 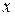 , в которой выполняются условия теоремы существования и единственности решения.
, в которой выполняются условия теоремы существования и единственности решения.
Определение 1.5. Частным решением ДУ называется любая функция 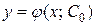 , которая получается из общего решения
, которая получается из общего решения 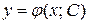 , если в последнем произвольной постоянной
, если в последнем произвольной постоянной 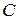 придать определенное значение
придать определенное значение 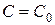 при начальном условии
при начальном условии 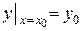 . Соотношение
. Соотношение 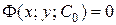 называется в этом случае частным интегралом ДУ.
называется в этом случае частным интегралом ДУ.
Пример 1.1. Для уравнения первого порядка 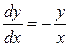 общим решением будет семейство функций
общим решением будет семейство функций 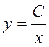 (это можно проверить простой подстановкой в уравнение).
(это можно проверить простой подстановкой в уравнение).
Найдем частное решение (решим задачу Коши), удовлетворяющее следующему начальному условию: 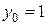 при
при 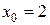 . Подставляя эти значения
. Подставляя эти значения 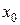 и
и 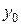 в формулу
в формулу 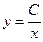 , получаем
, получаем 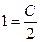 или
или 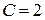 . Следовательно, искомым частным решением будет функций
. Следовательно, искомым частным решением будет функций 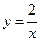 .
.
,
Определение 1.6.График частного решения ДУ называется интегральной кривой. Общему решению 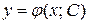 соответствует семейство интегральных кривых.
соответствует семейство интегральных кривых.
Таким образом, отыскание частного решения сводится к тому, что из семейства интегральных кривых нужно выбрать ту, которая проходит через точку 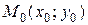 .
.
Решить или, как часто говорят, проинтегрировать ДУ – значит:
1) найти его общее решение или общий интеграл (если начальные условия не заданы);
2) найти его частное решение (частный интеграл), которое удовлетворяет заданным начальным условиям (если таковы имеются).
Дадим геометрическую интерпретацию ДУ первого порядка.
Пусть дано ДУ, разрешенное относительно производной, т.е. 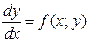 , и пусть
, и пусть 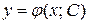 есть общее решение данного уравнения. Это общее уравнение определяет семейство интегральных кривых на плоскости
есть общее решение данного уравнения. Это общее уравнение определяет семейство интегральных кривых на плоскости 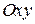 .
.
Данное ДУ для каждой точки 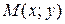 определяет значение производной
определяет значение производной 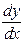 , т.е. угловой коэффициент касательной к интегральной кривой, проходящей через эту точку. Таким образом, ДУ
, т.е. угловой коэффициент касательной к интегральной кривой, проходящей через эту точку. Таким образом, ДУ 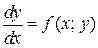 дает совокупность направлений или, как говорят, определяет поле направлений на плоскости
дает совокупность направлений или, как говорят, определяет поле направлений на плоскости 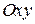 .
.
Следовательно, с геометрической точки зрения задача интегрирования ДУ заключается в нахождении кривых, направление касательных к которым совпадает с направлением поля в соответствующих точках.
Кривая, во всех точках которой направление поля одинаково, т.е. 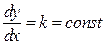 , называется изоклиной. При различных значениях
, называется изоклиной. При различных значениях 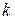 получаем различные изоклины. Построив семейство изоклин, можно приближенно построить семейство интегральных кривых. Говорят, что, зная изоклины, можно качественно определить расположение интегральных кривых на плоскости.
получаем различные изоклины. Построив семейство изоклин, можно приближенно построить семейство интегральных кривых. Говорят, что, зная изоклины, можно качественно определить расположение интегральных кривых на плоскости.
Пример 1.2. С помощью изоклин начертить вид интегральных кривых ДУ
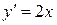 .
.
Решение. Уравнение изоклин этого ДУ будет 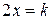 , т.е. изоклинами здесь будут
, т.е. изоклинами здесь будут
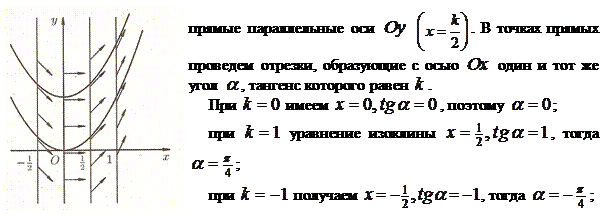
при 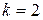 уравнение изоклины
уравнение изоклины 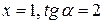 , тогда
, тогда 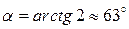 .
.
Построив четыре изоклины и отметив на каждой из них ряд стрелочек, наклоненных к оси 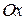 под определенным углом (см. рисунок), по их направлениям строим линии. Они, как видно, представляют собой семейство парабол вида
под определенным углом (см. рисунок), по их направлениям строим линии. Они, как видно, представляют собой семейство парабол вида 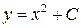 .
.
,
