Несобственные интегралы с бесконечными пределами
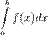
, f(x) –непрерывна [a,b]
Предполагаем:
1) f(x) –непрерывна [a,b]
2) [a,b] – конечны
Предположим нарушение 2-ого условия. f(x) –непрерывна [a,+∞]
a≤B<+∞
на любом отрезке [a,B] f(x) – непрерывна, тогда существует интеграл ∫f(x)dx
Несобственным интегралом от функции f(x) с бесконечным верхним пределом называется 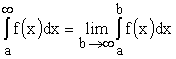 (1)
(1)
Если этот предел существует и конечен, то интеграл (1) называется сходящимся. В противном случае – расходящимся.
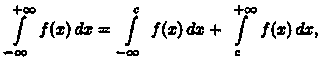
(3)
Интеграл (3) называется сходящимся, если сходится 2 интеграла в формуле (3) и называются расходящимися, если расходится хотя бы один из них
_
Несобственные интегралы сот неограниченных ф-ций.
y=f(x), a≤x≤b, f(x)- непрерывна, x ? [a, +∞], x=b, f(x) терпит разрыв 2 рода.
f(b)= ∞. f(x) непрерывна на любом отрезке. f(x) –непрерывна [a,b-e]
Несобственный интеграл от f(x) неогран. на [a,b] называется пределом
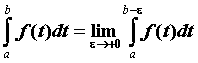
Если у интеграла существует конечный предел, то он называется сходящимся. 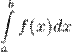 (2)
(2)
Аналогично определяем: f(x) –непрерывна [a,b], f(a)= ∞ разрыв 2 рода.
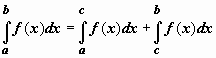
x=c(x=a, x=b) назыв. особыми точками, а несобств. интегралы от неогранич. функции называются интегралами 2-ого рода
_
Диф уравнения(ДУ). Основные понятия
Соотношения вида f(x,y,y’,…, yn)=0 (1), кот. Связывает независимую переменную х, y=y(x) – независимую ф. и ее производные, наз. диф уравнением предела n.
Порядок старшей производной - порядок ДУ
Опр. Решением ДУ-1 наз ф. y=y(x), кот. при подстановке в уравнение (1) обращает его в тождество.
График решения ДУ наз интегральной кривой.
Одно отдельно взятое решение ДУ наз. частным решением. Частное решение в неявном виде наз частным интегралом.
Общим решением ДУ наз ф. y=y(x, с1,с2,…) зависящая от n независимых произвольных постоянных, кот. при соответствующем выборе значений произвольных постоянных является решением ДУ
Нахождение решений ДУ наз. его интегрированием. Проинтегрировать ДУ значит найти все его решения.
_
ДУ-1. Задача Коши.
ДУ 1ого порядка имеет вид F(x,y,y’)=0 (1)
Если можно в уравнении (1) выразить производную через независимую х и ф. у, то y’=f(x,y) (2)
y’=dy/dx, dy/dx=f(x,y), dy-f(x,y)dx=0
Вводим обозначение p(x,y)dx+Q(x,y)dy=0 (3)–диф.форма ду-1
Теорема Коши: Если для уравнения y’=f(x,y) производная df/dy и ф. f(x,y) непрерывна в нек. открытой области D, то сущ., при том единственное решение y=y(x) этого ду, уд. условию y(x0)=y0 для любой (х0 у0) принадлежащей D
Если 2 решения у=у1(х) и у=у2(х) совпадают хотя бы при одном значении х=х0, у=у0, то у1(х)=у2(х) для всех допустимых значений аргумента.
Общим решением ДУ-1 наз. Ф. y=f(x,y) зависящая от одной производной и уд. 2ум условиям:
1) y=f(x,c)
2) х=х0, у=у0 ,(х0 у0) принадлежат D, существует c=c0 , что y=f(x,c0) является решение ду
Задача Коши:
Среди всех решений ДУ y’=f(x,y) выделить решения, удовлетворяющие условиям y(x0)=y0 и y=y(x)
Геометрически: среди всех интегральных кривых уравнения (2) выделить кривую, проходящую через точку (х0,у0)
_
