Несобственные интегралы с бесконечными пределами (несобственные
интегралы 1-го рода)
Пусть функция f(x) определена и непрерывна при х ≥ а. Тогда интеграл 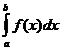 имеет смысл при любом b > a и является непрерывной функцией аргумента b.
имеет смысл при любом b > a и является непрерывной функцией аргумента b.
Определение 15.1. Если существует конечный предел
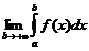 , (15.1)
, (15.1)
то его называют несобственным интегралом 1-го рода от функции f(x) на интервале 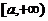 и обозначают
и обозначают 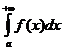 . Таким образом, по определению
. Таким образом, по определению
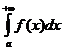 =
= 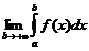 . (15.2)
. (15.2)
При этом говорят, что несобственный интеграл существует или сходится. Если же не существует конечного предела (15.1), несобственный интеграл не существует или расходится.
 y Повторим, что геометрической интерпрета-
y Повторим, что геометрической интерпрета-


 y=f(x) цией несобственного интеграла 1-го рода
y=f(x) цией несобственного интеграла 1-го рода


 является площадь неограниченной области,
является площадь неограниченной области,
 расположенной между графиком функции
расположенной между графиком функции


 y=f(x) , прямой х = а и осью Ох.
y=f(x) , прямой х = а и осью Ох.
a b
Замечание. Аналогичным образом можно определить и несобственные интегралы 1-го рода для других бесконечных интервалов:
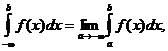
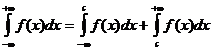 (15.3)
(15.3)
В частности, последний интеграл существует только в том случае, если сходятся оба интеграла, стоящие в правой части равенства.
Часто достаточно бывает только установить сходимость или расходимость несобственного интеграла и оценить его значение.
Лемма.
Если 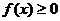 на интервале [a, +∞), то для сходимости интеграла
на интервале [a, +∞), то для сходимости интеграла 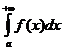 необходимо и достаточно, чтобы множество всех интегралов
необходимо и достаточно, чтобы множество всех интегралов 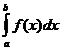 (b > a) было ограничено сверху, то есть чтобы существовала такая постоянная c > 0, чтобы
(b > a) было ограничено сверху, то есть чтобы существовала такая постоянная c > 0, чтобы 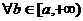 выполнялось неравенство
выполнялось неравенство 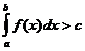 . (15.4)
. (15.4)
Доказательство.
Рассмотрим функцию 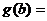
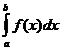 и покажем, что в условиях леммы она монотонно возрастает на [a, +∞). Действительно, при
и покажем, что в условиях леммы она монотонно возрастает на [a, +∞). Действительно, при 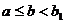
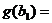
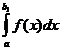 =
= 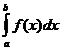 +
+
+ 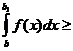
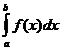 =g(b), так как при
=g(b), так как при 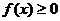
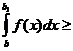 0. Следовательно, функция g(b) монотонно возрастает и ограничена сверху, поэтому она имеет конечный предел при
0. Следовательно, функция g(b) монотонно возрастает и ограничена сверху, поэтому она имеет конечный предел при 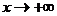 , что по определению означает существование интеграла
, что по определению означает существование интеграла 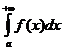 .
.
Теорема 15.1 (признак сравнения). Пусть 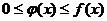 при
при 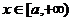 . Тогда:
. Тогда:
1) если интеграл 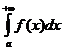 сходится, то сходится и интеграл
сходится, то сходится и интеграл 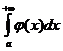 ;
;
2) если интеграл 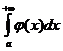 расходится, то расходится и интеграл
расходится, то расходится и интеграл 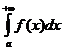 .
.
Доказательство.
Из условия теоремы следует, что 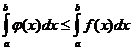
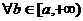 . Поэтому, если интегралы
. Поэтому, если интегралы 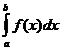 ограничены сверху (по лемме), то сверху ограничены и интегралы
ограничены сверху (по лемме), то сверху ограничены и интегралы 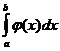 , следовательно,
, следовательно, 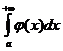 сходится (по той же лемме). Если же интеграл
сходится (по той же лемме). Если же интеграл 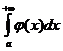 расходится, то, если бы интеграл
расходится, то, если бы интеграл 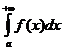 сходился, то по ранее доказанному
сходился, то по ранее доказанному 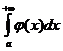 должен был бы сходиться, что противоречит сделанному предположению. Значит, в этом случае
должен был бы сходиться, что противоречит сделанному предположению. Значит, в этом случае 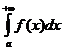 расходится. Теорема полностью доказана.
расходится. Теорема полностью доказана.
Следствие.
Пусть 
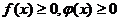 на [a,∞),
на [a,∞), 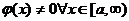 и существует конечный или бесконечный предел
и существует конечный или бесконечный предел 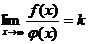 , то:
, то:
а) если интеграл 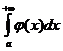 сходится и
сходится и 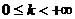 , то сходится и интеграл
, то сходится и интеграл 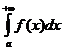 ;
;
б) если интеграл 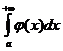 расходится и
расходится и 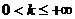 , то интеграл
, то интеграл 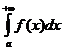 тоже расходится.
тоже расходится.
В частности, если k = 1, то есть функции f(x) и φ(х) эквивалентны при 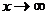 , то интегралы
, то интегралы 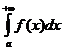 и
и 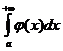 сходятся и расходятся одновременно.
сходятся и расходятся одновременно.
При применении признака сравнения удобно сравнивать подынтегральную функцию с функцией 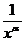 , α > 0, для которой сходимость или расходимость соответствующего несобственного интеграла легко установить непосредственно. Пусть
, α > 0, для которой сходимость или расходимость соответствующего несобственного интеграла легко установить непосредственно. Пусть 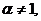 тогда
тогда
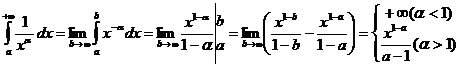 . При α = 1
. При α = 1
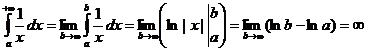 . Следовательно,
. Следовательно, 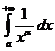 сходится при α > 1 и расходится при α ≤ 1.
сходится при α > 1 и расходится при α ≤ 1.
Пример.
Исследуем на сходимость 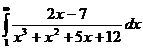 . При
. При 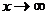 подынтегральная функция эквивалентна
подынтегральная функция эквивалентна 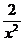 . Таким образом, α = 2 > 1, и данный интеграл сходится.
. Таким образом, α = 2 > 1, и данный интеграл сходится.
