Задачи для самостоятельного решения. В задачах 3.3.1–3.3.2 решить линейные системы а) по формулам Крамера
В задачах 3.3.1–3.3.2 решить линейные системы а) по формулам Крамера, б) матричным способом, в) методом Гаусса.
3.3.1. 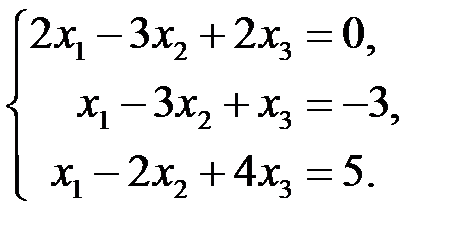 | 3.3.2.  |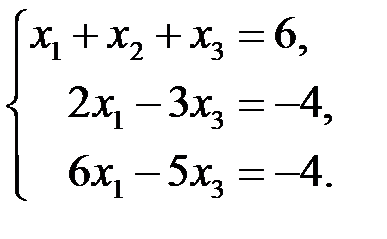
В задачах 3.3.3–3.3.4 решить линейные системы матричным способом.
3.3.3. 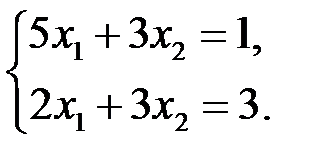 | 3.3.4.  |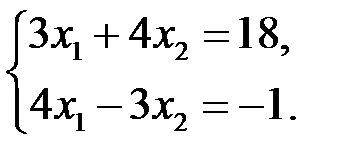
В задачах 3.3.5–3.3.10 решить линейные системы методом Гаусса.
3.3.5. 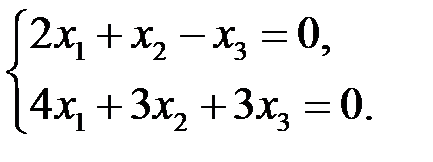 | 3.3.6.  |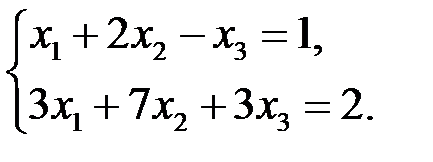
3.3.7. 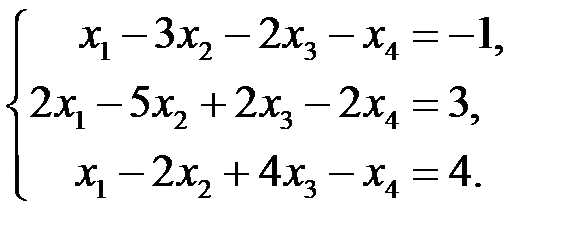 | 3.3.8.  |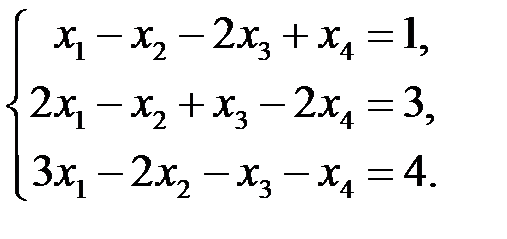
РАНГ МАТРИЦЫ
Основные понятия и формулы
Понятие ранга
В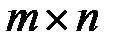 
-матрице 
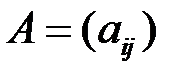выберем 
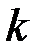строк с номерами 
и столько же столбцов с номерами 
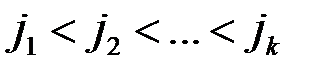. Определитель матрицы из элементов, находящихся в этих строках и столбцах, обозначим 
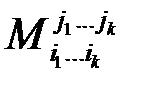и назовем минором 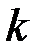-го порядка матрицы 
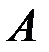. Например, у матрицы 
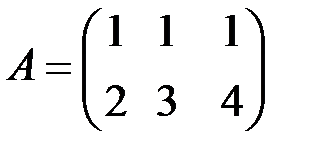три минора 2-го порядка:
, 
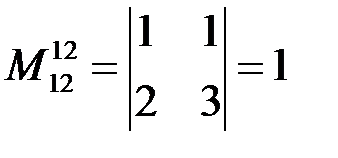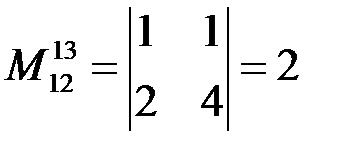и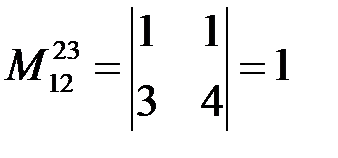 
.
Рангом (ненулевой) матрицы называется наибольший из порядков ненулевых миноров. Ранг матрицы 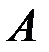мы будем обозначать 
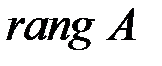. Таким образом, равенство 
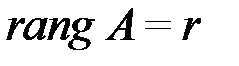означает, что у матрицы 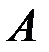есть ненулевой минор порядка 
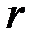, а все миноры больших порядков, если они имеются, равны нулю (см. пример 4.2.1). Ранг характеризует степень «вырожденности» матрицы. Например, для квадратной матрицы 
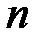-го порядка крайние случаи: нулевая матрица 
самая «вырожденная», у нее все миноры нулевые и естественно считать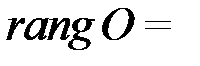 
0; и невырожденная матрица 
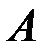с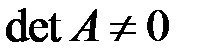 
, ее ранг 
.
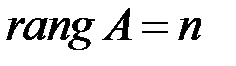Так как миноров у матрицы даже небольших размеров много, то нахождение ранга по определению связано с громоздкими вычислениями. Для нахождения ранга можно применять элементарные преобразования матриц, аналогичные элементарным преобразованиям систем, описанным в п. 3.1.3:
а) перестановки любых двух строк местами;
б) прибавление к строке другой строки, умноженной на число;
в) удаление строки, состоящей из нулей;
г) те же действия, что и в пунктах а)–в), для столбцов.
При этих преобразованиях ненулевые миноры переходят в ненулевые и потому они не меняют ранга. После преобразований получим матрицу вида
,
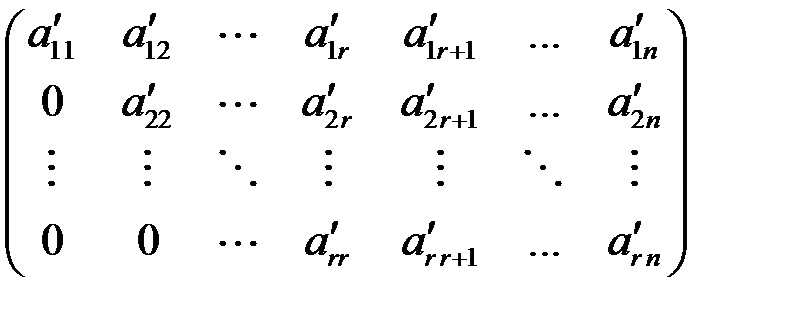у которой минор
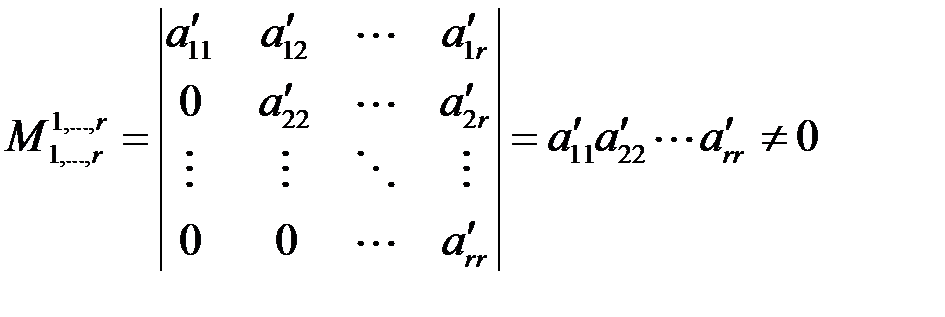
и потому ранг равен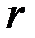 
(см. пример 4.2.2).
Матрицы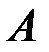 
и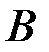 
называются эквивалентными (обозначение 
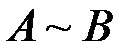), если у них одинаковый ранг: 
.
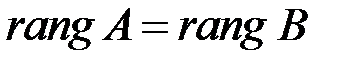Совместность линейной системы и ранг
Для произвольной линейной системы (3.1) из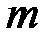 
уравнений с 
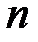неизвестными, наряду с основной матрицей системы 
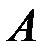размера 
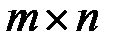, рассмотрим расширенную матрицу 
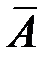размера 
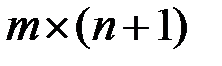, полученную добавлением к 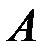справа столбца 
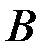свободных членов. Ясно, что 
.
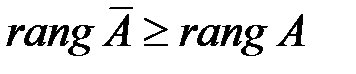Теорема Кронекера-Капелли. Линейная система совместна тогда и только тогда, когда ранги основной и расширенной матриц системы совпадают: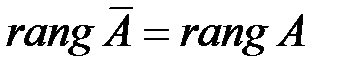 
.
Можно показать, что при решении системы методом Гаусса число уравнений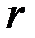 
в преобразованной системе (3.5) является рангом матриц 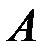и .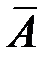
Примеры решения задач
4.2.1.Пользуясь определением, найти ранги матриц
, 
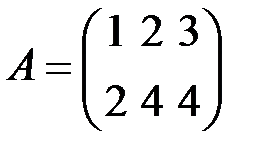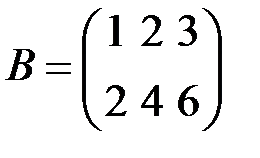и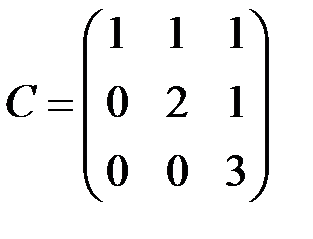 
.
◄ 1) Так как ранг матрицы – наибольший из порядков ненулевых миноров, то надо начать с нахождения миноров самого большого порядка – второго.
Найдем минор второго порядка матрицы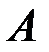 
, из элементов, взятых из строк с номерами 1 и 2 и столбцов с номерами 1 и 2: 
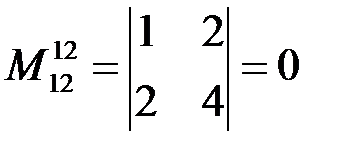. Он, увы, нулевой. Найдем еще один минор второго порядка 
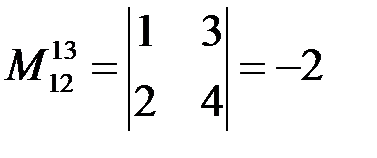. Он нулю не равен. Поэтому 
.
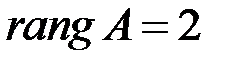2) У матрицы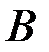 
все миноры наибольшего – второго порядка – нулевые:
, 
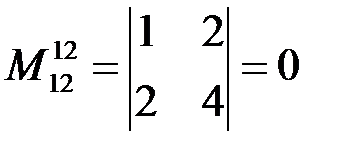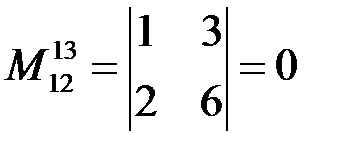и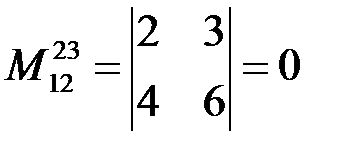 
.
Поэтому надо проверять миноры первого порядка – элементы матрицы. Например,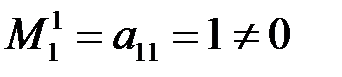 
. Поскольку есть ненулевой минор первого порядка, а все миноры большего порядка нулевые, то 
.
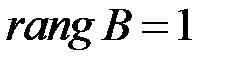3) У матрицы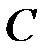 
единственный минор наибольшего – третьего порядка 
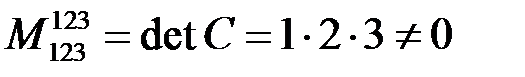. Поэтому 
. ►
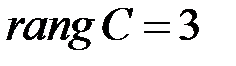4.2.2.Найти ранг матрицы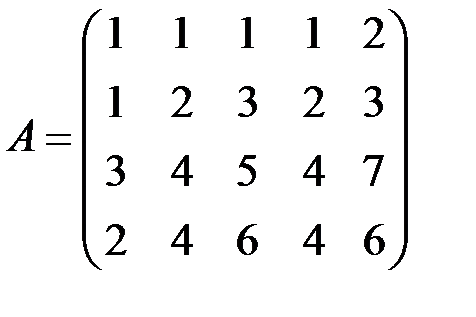 
.
◄ Будем делать элементарные преобразования матриц, не меняющие ранга:
.
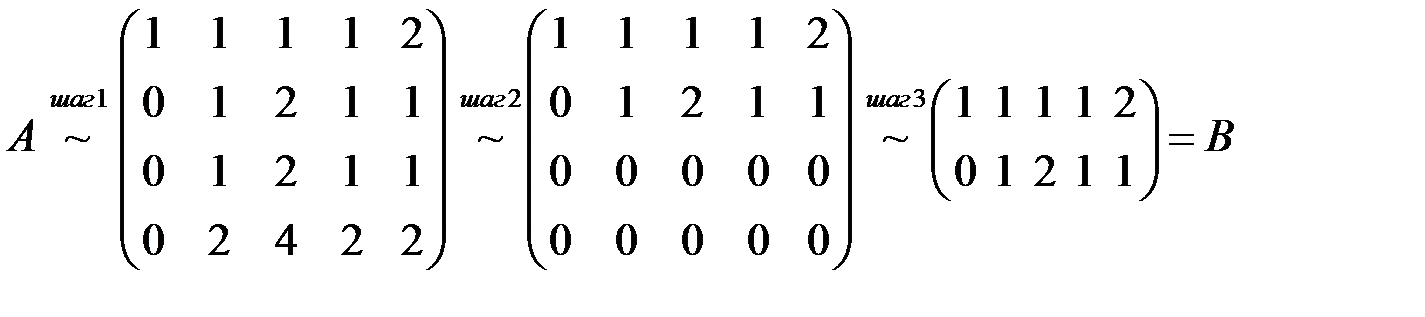Шаг 1. Первую строку оставили неизменной, ко второй прибавили первую, умноженную на (–1), к третьей прибавили первую, умноженную на (–3), к четвертой прибавили первую, умноженную на (–2).
Шаг 2. Первую и вторую строки оставили неизменными, к третьей прибавили вторую, умноженную на (–1), к четвертой прибавили вторую, умноженную на (–2).
Шаг 3. Удалили нулевые строки.
В итоге получили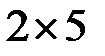 
-матрицу 
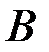, эквивалентную матрице 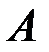, у которой минор второго порядка 
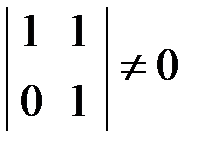. Поэтому 
.
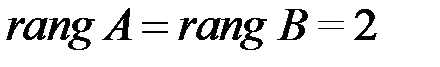Заметим, что, если бы мы попытались найти ранг по определению, то нам бы пришлось сначала вычислить все 10 миноров четвертого порядка, которые равны нулю, потом 20 миноров третьего порядка, тоже равные нулю, пока не обнаружим ненулевой минор второго порядка. ►
4.2.3.При каких значениях параметра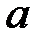 
линейная система
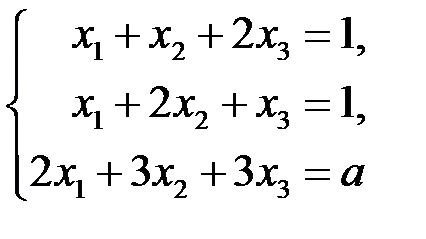
совместна?
◄ Выпишем расширенную матрицу системы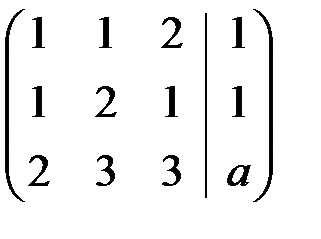 
.
Слева от вертикальной черты у нас выписана и основная матрица. Будем вычислять одновременно ранги обеих матриц, делая элементарные преобразования только со строками:
.
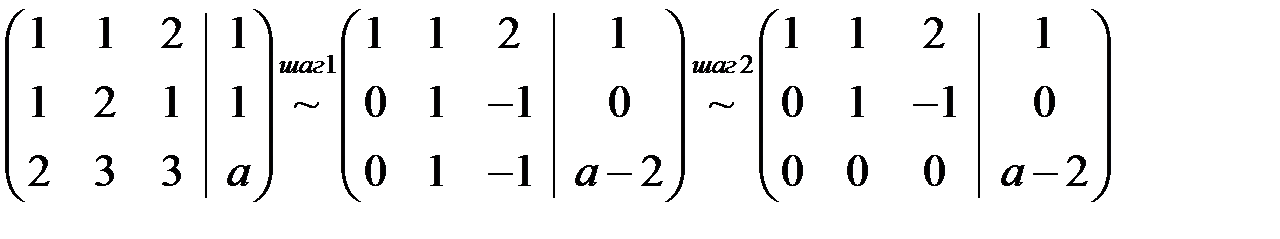Шаг 1. Первую строку оставили неизменной, ко второй прибавили первую, умноженную на (–1), к третьей прибавили первую, умноженную на (–2).
Шаг 2. Первую и вторую строки оставили неизменными, к третьей прибавили вторую, умноженную на (–1).
У преобразованной основной матрицы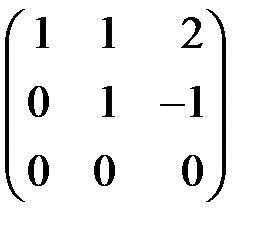 
можно удалить нулевую строку и ее ранг – 2. При 
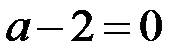у преобразованной расширенной матрицы тоже нулевая строка и ее ранг – 2. По теореме Кронекера-Капелли при 
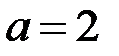система совместна. При 
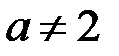минор третьего порядка расширенной матрицы
.
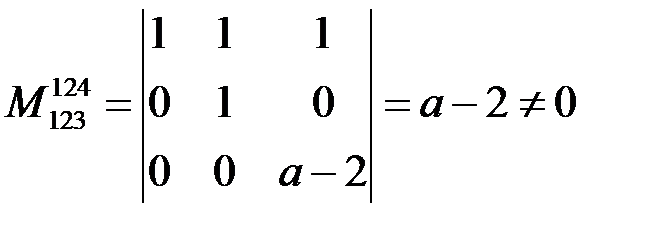Поэтому ранг расширенной матрицы равен 3. Он не совпадает с рангом основной матрицы. Согласно теореме Кронекера-Капелли при 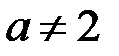система несовместна.
Наши действия с расширенной матрицей можно рассматривать как прямой ход метода Гаусса (см. п. 3.1.3). При 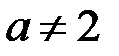получаем уравнение 
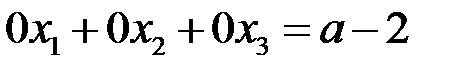, не имеющее решения, что влечет несовместность системы. ►