Классификация точек разрыва функции

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.

Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке

• Существуют левосторонний предел 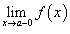и правосторонний предел ;
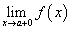• Эти односторонние пределы конечны.

При этом возможно следующие два случая:

• Левосторонний предел и правосторонний предел равны друг другу:

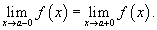
Такая точка называется точкой устранимого разрыва.

• Левосторонний предел и правосторонний предел не равны друг другу:

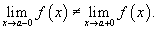
Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов 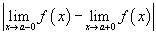называется скачком функции.

Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.

Пример 1

Исследовать функцию 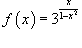на непрерывность.

Решение.

Данная функция не определена в точках x = −1 и x = 1. Следовательно, функция имеет разрывы в точкахx = ±1. Чтобы определить тип разрыва, вычислим односторонние пределы в этих точках.

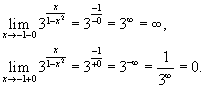
Поскольку левосторонний предел при x = −1 равен бесконечности, то данная точка является точкой разрыва второго рода.

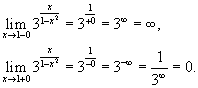
Аналогично, левосторонний предел в точке x = 1 равен бесконечности. Эта точка также является точкой разрыва второго рода.

Пример 2

Показать, что функция 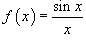имеет устранимый разрыв в точке x = 0.

Решение.

Очевидно, данная функция не определена при x = 0. Поскольку sin x является непрерывной функцией для всехx, то искомая функция 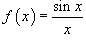также непрерывна при всех x за исключением точки x = 0.
Так как 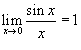, то в данной точке существует устранимый разрыв. Мы можем сконструировать новую функцию

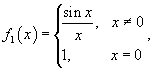
которая будет непрерывной при любом действительном x.

Пример 3

Найти точки разрыва функции 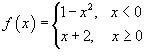, если они существуют.

Решение.

Данная функция существует при всех значениях x, однако она состоит из двух различных функций и, поэтому, не является элементарной. Исследуем "поведение" этой функции вблизи точки x = 0, где ее аналитическое выражение изменяется.

Вычислим односторонние пределеы при x = 0.

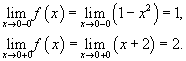
Следовательно, функция имеет точку разрыва первого рода при x = 0. Скачок функции в этой точке равен

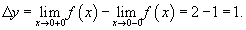
При всех других значениях x функция является непрерывной, поскольку обе составляющие функции слева и справа от точки x = 0 представляют собой элементарные функции без точек разрыва.

Пример 4

Найти точки разрыва функции 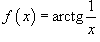, если они существуют.

Решение.

Данная элементарная функция определена для всех x, исключая точку x = 0, где она имеет разрыв. Найдем односторонние пределы в этой точке.

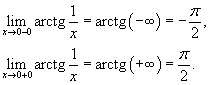
Видно, что в точке x = 0 существует разрыв первого рода (рисунок 2).

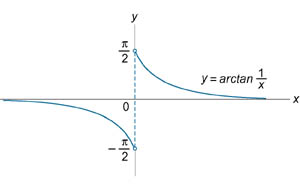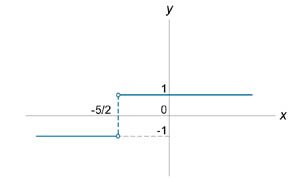Рис.2		Рис.3

Пример 5

Найти точки разрыва функции 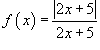, если таковые существуют.

Решение.

Функция определена и непрерывна при всех x, за исключением точки 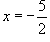, где существует разрыв. Исследуем точку разрыва.

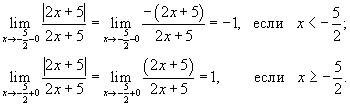
Так как значения односторонних пределов конечны, то, следовательно, в точке 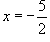существует разрыв первого рода. График функции схематически показан на рисунке 3.

42.

43.

Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897) - немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке 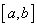выполняется условие - .

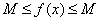Доказательство этого свойства основано на том, что функция, непрерывная в точке 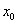, ограничена в некоторой ее окрестности, а если разбивать отрезок 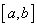на бесконечное количество отрезков, которые “стягиваются” к точке 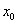, то образуется некоторая окрестность точки .

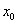Свойство 2: Функция, непрерывная на отрезке 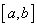, принимает на нем наибольшее и наименьшее значения.

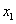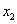Т.е. существуют такие значения и , что 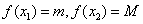, причем .

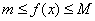Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например - ).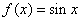

Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.

Свойство 3: (Вторая теорема Больцано - Коши). Функция, непрерывная на отрезке 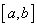, принимает на этом отрезке все значения между двумя произвольными величинами.

Свойство 4: Если функция 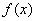непрерывна в точке 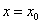, то существует некоторая окрестность точки 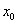, в которой функция сохраняет знак.

Свойство 5: (Первая теорема Больцано (1781-1848) - Коши). Если функция 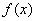- непрерывная на отрезке 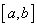и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где .

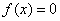Т.е. если 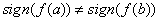, то .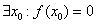

Определение. Функция 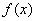называется равномерно непрерывной на отрезке 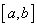, если для любого 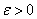существует 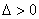такое, что для любых точек 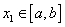и 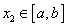таких, что 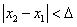верно неравенство .

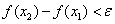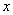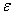Отличие равномерной непрерывности от “обычной” в том, что для любого e существует свое , не зависящее от , а при “обычной” непрерывности зависит от и .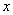

Свойство 6: Теорема Кантора (Кантор Георг (1845-1918) - немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем. (Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)

Свойство 7: Если функция 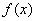определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция 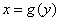тоже однозначна, монотонна и непрерывна.

Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть. 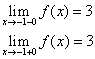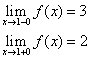в точке 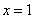функция непрерывна в точке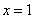

точка разрыва 1 - го рода