Теорема Лопиталя. Раскрытие неопределенностей по правилу Лопиталя

(Лопиталь (1661-1704) – французский математик)

К разряду неопределенностей принято относить следующие соотношения:

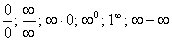
Теорема (правило Лопиталя). Если функции f(x) и g(x) дифференцируемы в вблизи точки а, непрерывны в точке а, g(x) отлична от нуля вблизи а и f(a) = g(a) = 0, то предел отношения функций при ха равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует.

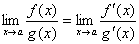
Доказательство. Применив формулу Коши, получим:

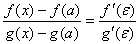
[an error occurred while processing this directive]

где  - точка, находящаяся между а и х. Учитывая, что f(a) = g(a) = 0:

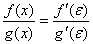
Пусть при ха отношение 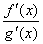стремится к некоторому пределу. Т.к. точка  лежит между точками а и х, то при ха получим а, а следовательно и отношение 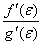стремится к тому же пределу. Таким образом, можно записать:

.

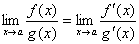Теорема доказана.

45. Свойства функций, дифференцируемых на интервале: Теорема Ролля. Теорема Коши. Теорема Лагранжа.

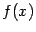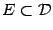Пусть функция определена на некотором множестве , и . Назовём точку 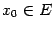точкой максимума функции 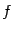на множестве 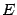, если при всех 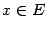выполняется неравенство 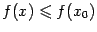, и точкой минимума, если при всех 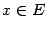выполняется неравенство .

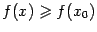Точка 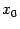, являющаяся либо точкой максимума, либо точкой минимума, называется точкой экстремума.

Теорема 5.2 (Ролля)Пусть функция 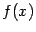дифференцируема на интервале 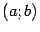, непрерывна в точках 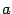и 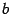и принимает в этих точках значение 0: 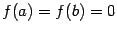. Тогда найдётся хотя бы одна точка 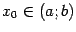, в которой .

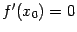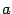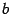Замечание 5.2 Это утверждение можно переформулировать так: между двумя корнями и дифференцируемой функции 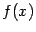обязательно найдётся корень её производной 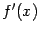(то есть точка 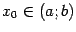, такая что 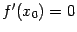). Условие 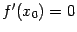означает, что касательная, проведённая к графику 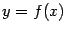при 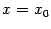, расположена горизонтально.

Заметим также, что теорема Ролля не утверждает, что корень 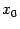-- единственный корень производной на интервале 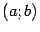; на этом интервале может находиться несколько корней производной.

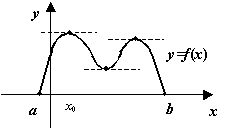
Рис.5.4.Между двумя корнями дифференцируемой функции лежит хотя бы один корень её производной

Доказательство теоремы Ролля. Так как при наших предположениях функция 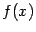непрерывна на отрезке 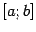, то она принимает своё максимальное значение 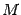и минимальное значение 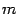в некоторых точках 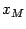и 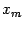этого отрезка.

Рассмотрим два случая. Если 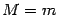, то наибольшее и наименьшее значения функции совпадают, и, следовательно, функция постоянна на отрезке 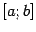: 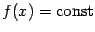. Значит, 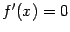при всех 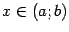, и в качестве 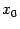в этом случае можно взять любую точку 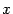интервала .

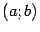Если же 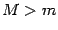, то либо 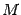, либо 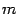отлично от 0 и, следовательно, либо точка 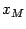, либо точка 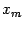не совпадает с концами отрезка 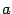и 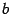, то есть лежит внутри интервала 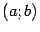. Пусть, для определённости, 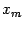-- внутренняя точка интервала. Тогда, по теореме Ферма, 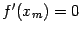, поскольку по предположению доказываемой теоремы, 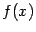имеет производную во всех точках интервала 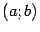и, следовательно, в точке 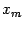. Итак, в этом случае точку 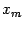можно взять в качестве искомой точки 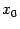: тогда .

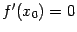Теорема 5.3 (Лагранжа) Пусть функция 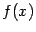дифференцируема на интервале 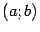и непрерывна в точках 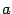и 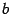. Тогда найдётся такая точка 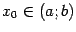, что

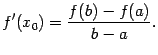(5.1)

Замечание 5.3 Формулу (5.1) можно записать в виде

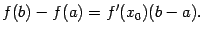(5.2)

Если считать, что аргументу 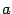придано приращение 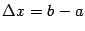, то функция получает приращение 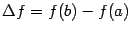. (При этом мы не считаем, что 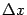и 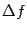стремятся к 0, то есть это конечные, а не бесконечно малые, приращения.) При этих обозначениях формулу (5.2) мы можем записать в виде

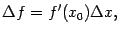
в котором участвуют конечные приращения аргумента и функции. Поэтому формулу (5.2) называют формулой конечных приращений.

Доказательство теоремы Лагранжа. Дадим сначала геометрическую иллюстрацию теоремы. Соединим конечные точки графика 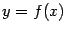на отрезке 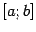хордой. Конечные приращения 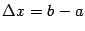и 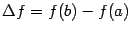-- это величины катетов треугольника, гипотенузой которого служит проведённая хорда.

Рис.5.5.Касательная в некоторой точке параллельна хорде

Отношение конечных приращений и -- это тангенс угла наклона хорды. Теорема утверждает, что к графику дифференцируемой функции можно провести в некоторой точке 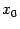касательную, которая будет параллельна хорде, то есть угол наклона касательной 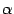( 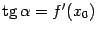) будет равен углу наклона хорды 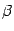( 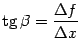). Но наличие такой касательной геометрически очевидно.

Заметим, что проведённая хорда, соединяющая точк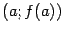и и 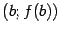-- это график линейной функции 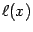. Поскольку угловой коэффициент этой линейной функции равен, очевидн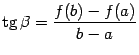о, , то

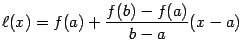
(мы учли то, что график линейной функции проходит через точку ).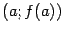

Сведём доказательство к применению теоремы Ролля. Для этого введём вспомогательную функцию 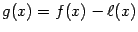, то есть

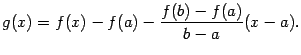
Заметим, что 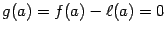и 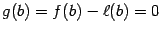(по построению функции 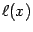). Так как линейная функция 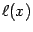дифференцируема при всех 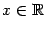, то функция 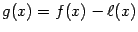удовлетворяет, тем самым, всем свойствам, перечисленным в условии теоремы Ролля. Поэтому найдётся такая точка 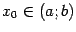, что .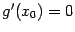

Заметим теперь, что

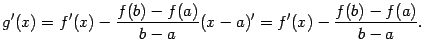
Значит, равенство 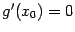можно переписать в виде

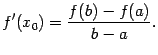
Таким образом, мы доказали формулу (5.1).

Из теоремы Лагранжа вытекает утверждение, обратное к тому, что производная постоянной есть 0, а именно:

Следствие 5.1 Пусть на интервале 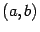функция 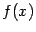имеет производную 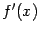, тождественно равную 0: 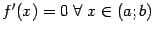. Тогда 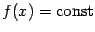на интервале .

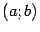Доказательство. Заметим для начала, что непрерывность функции 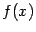в любой точке интервала 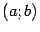следует из дифференцируемости в этой точке. Значит, теорему Лагранжа можно применить к функции 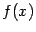на любом отрезке .

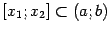Возьмём любые две точки 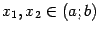, такие что 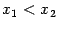, и выпишем для функции 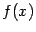на отрезке 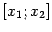формулу конечных приращений: 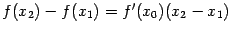, при некотором 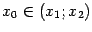. Но в любой точке производная по предположению равна 0, в том числе 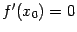. Отсюда 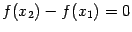, или 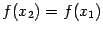. Обозначим это общее значение через 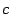. Выбирая произвольно точку 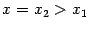, получим, что 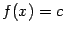при всех 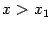; выбирая произвольно точку 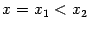, -- что 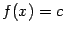при всех 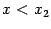. Но это означает, что 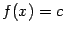при всех .

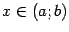Теорема 5.4 (Коши) Пусть функци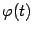и и 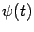дифференцируемы на интервале 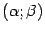и непрерывны пр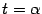и и 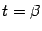, причём 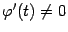при всех 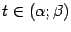. Тогда в интервале 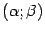найдётся такая точка 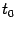, что

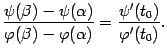
Доказательство. Докажем сначала, что 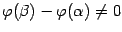, то есть что дробь в левой части формулы имеет смысл. Действительно, для этой разности можно записать формулу конечных приращений:

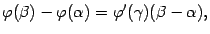
при некотором 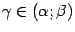. Но в правой части этой формулы оба множителя отличны от нуля.

Для доказательства теоремы применим тот же приём, что при доказательстве теоремы Лагранжа: введём вспомогательную функцию

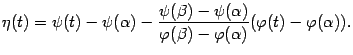
Функция 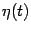, очевидно, является дифференцируемой при всех 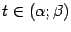и непрерывной в точках 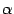и 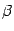, поскольку этими свойствами обладают функци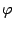и и 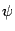. Кроме того, очевидно, что при 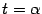получается 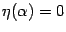. Покажем, что и :

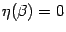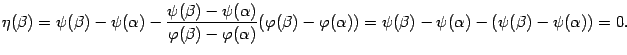
Значит, функция 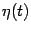удовлетворяет на отрезке 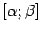условиям теоремы Ролля. Поэтому существует такая точка 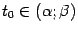, что .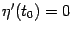

Вычислим теперь производную функции :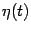

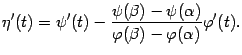
Получаем, что

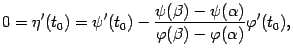
откуда получаем утверждение теоремы:

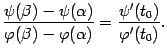
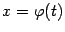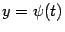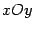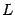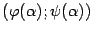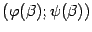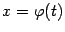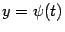Замечание 5.4 Можно считать функции и координатами движущейся на плоскости точки, которая описывает линию , соединяющую начальную точку с конечной точкой . (Тогда уравнения и параметрически задают некоторую зависимость 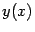, графиком которой служит линия .)

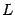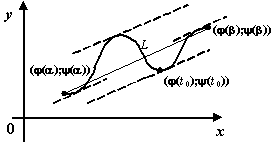
Рис.5.6.Хорда параллельна некоторой касательной к кривой

Отношение 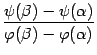, как нетрудно видеть из чертежа, задаёт тогда угловой коэффициент хорды, соединяющей точк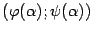и и 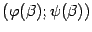. В то же время, по формуле производной функции, заданной параметрически, имеем: 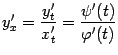. Значит, дробь 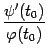-- это угловой коэффициент касательной к линии 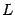в некоторой точке 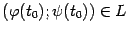. Тем самым утверждение теоремы означает, с геометрической точки зрения, что на линии 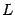найдётся точка, такая что проведённая в этой точке касательная параллельна хорде, соединяющей крайние точки линии. Но это -- то же самое утверждение, которое составляло геометрический смысл теоремы Лагранжа. Только в теореме Лагранжа линия 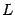была задана явной зависимостью 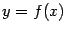, а в теореме Коши -- зависимостью, заданной в параметрической форме.

1. Частные производные и дифференциалы высших порядков для числовой функции нескольких переменных.

Частные производные функции нескольких переменных сами являются функциями этих переменных и могут иметь частные производные. Для исходной функции эти последние производные будут частными производными второго порядка. Так, для функции 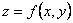двух независимых переменных можно определить (предполагается, что все производные существуют) четыре частные производные второго порядка, которые обозначаются символами

, ,

, .

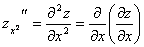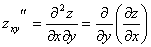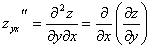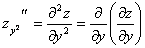Частные производные 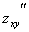и 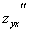, отличающиеся порядком дифференцирования, называются смешанными частными производными второго порядка.

Аналогично определяются частные производные третьего, четвертого и старших порядков.

Пример. Найти частные производные второго порядка функции .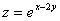

Имеем:

, ,,

, , , .

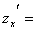
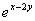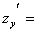
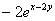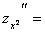
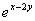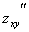
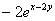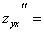
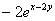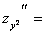
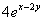Здесь 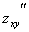= 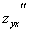. Оказывается, имеет место следующая теорема.

Теорема. Смешанные производные второго порядка равны, если они непрерывны: = .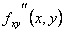

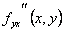Следствие. Смешанные производные высших порядков равны, если они непрерывны и получены в результате дифференцирования по одним и тем же переменным одинаковое число раз, но может быть в разной последовательность.

Покажем это на примере:

,

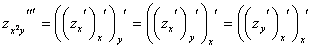т.е.

.

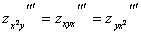Здесь мы дважды пользовались только что отмеченной теоремой: первый раз применительно к функции 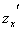(мы изменили порядок ее дифференцирования), второй раз использовали равенство 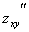= 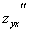. В общем случае схема рассуждений аналогична.
3.2
Признак полного дифференцирования.
Выясним, при каких условиях выражение 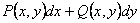, (1)

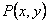где и 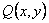непрерывны и вместе со своими частными производными первого порядка, является полным дифференциалом некоторой функции 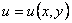, или, кратко, полным дифференциалом.

Теорема. Выражение (1) есть полный дифференциал тогда и только тогда, когда выполнено равенство

.
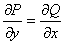3.3. Дифференциалы высших порядков.
Заметим прежде всего, что для функции нескольких переменных справедливы те же общие правила дифференцирования, что и для функции одной переменной:

I. , .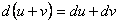

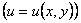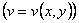II. .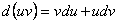

III. .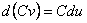

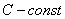IV. .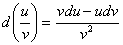

Пусть имеется функция 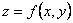независимых переменных xи y, обладающая непрерывными частными производными второго порядка. Рассмотрим ее полный дифференциал

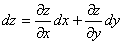
(dx
и dy – произвольные приращения), который назовем полным дифференциалом первого порядка (или, кратко, первым дифференциалом).

Так как 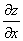и 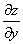по предложению имеют непрерывные частные производные первого порядка, то от функции 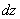, в свою очередь, можно взять полный дифференциал 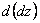. Так получим полный дифференциал второго порядка (или, кратко, второй дифференциал), который обозначается .

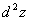Аналогично, потребовав существование непрерывных частных производных третьего, четвертого, п-го порядков, можно получить полные дифференциалы соответственно третьего, четвертого, п-ого порядков.

Найдем выражения для второго дифференциала через частные производные. Пользуясь правилами I, III (dx
и dy
не зависят от x
и y, т.е. рассматриваются как постоянные) и приведенной в п. 3.1 теоремой, можно записать:

(2)
(здесь , ).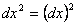

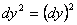Формула (2) обобщается на случай дифференциала п-го порядка.