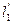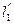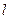Кривые второго порядка
Пример 1. Найти центр и радиус окружности, заданной уравнением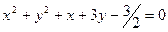 
.
Решение. Приведем исходное уравнение к виду (4.13). Для этого сгруппируем члены с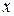 
и члены с 
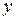, и выделим в скобках полные квадраты.
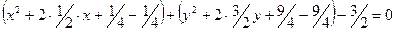, или
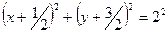- это уравнение окружности с центром в точке 
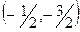и радиусом 2.
Пример 2. Найти координаты фокусов и эксцентриситет эллипса, описываемого уравнением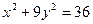 
.
Решение. Приведем уравнение к виду ( 4.14 ) разделив обе части уравнения 36
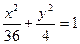, откуда 
, 
.
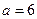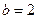Определяем расстояние фокусов от центра: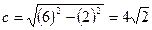 
.
Так как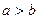 
то фокусы эллипса лежат на оси 
: 
, 
.
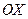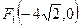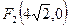Эксцентриситет данного эллипса определяем по формуле:
.
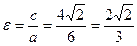Пример 3. Написать уравнение гиперболы, если ее фокусы находятся в точках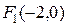 
, 
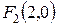, а длина ее действительной оси равна 1.
Решение. Для записи уравнения гиперболы в виде (4.15 ) необходимо знать величины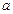 
и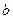 
. Величина 
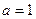по условию задачи (длина действительной оси). Определим величину .
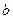Из условия задачи можно определить величину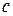 
. Это первая координата фокуса, то есть 
.
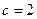По формуле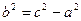 
определяем величину : 
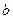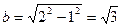
Подставляем в уравнение (4.15 ), получаем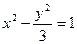 
.
Пример 4. Вывести каноническое уравнение параболы, если известно, что ее вершина расположена в начале координат, она расположена симметрично оси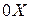 
, и проходит через точку 
.
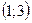Решение. По условию парабола симметрична оси 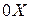и вершина расположена в начале координат, следовательно, для нахождения параметра параболы можно воспользоваться каноническим уравнением ( 4.16 ).
Подставим в уравнение (4.16 ) координаты точки, через которую проходит парабола: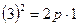 
, откуда 
.
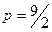Следовательно, уравнение параболы можно записать как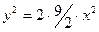 
; 
.
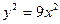Пример 5. Определить вид кривой второго порядка 
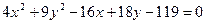
и её параметры .
Решение. Преобразуем уравнение линии, группируя члены с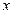 
и члены с 
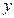, и вынося за скобки коэффициенты при квадратах:
,
;
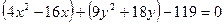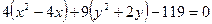выделим в скобках полные квадраты:
,
,
,
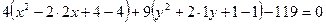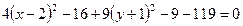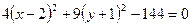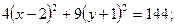
разделим обе части уравнения на (144):
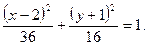
Получили уравнение эллипса (4.18) с центром в точке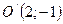 
.
Выполним параллельный перенос
.
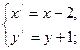
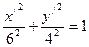Получили каноническое уравнение эллипса в систем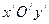е 
, где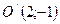 
- новое начало. Полуоси 
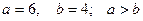, поэтому большая ось параллельна оси .
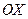Найдем фокусы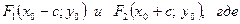 
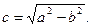
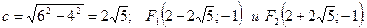
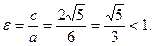
Вершины эллипса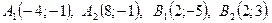 
Задачи для самостоятельного решения
1. Составить уравнение эллипса, полуоси которого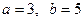 
, центр в точке (-2; 3)
2. Для гиперболы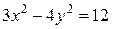 
найти действительную и мнимую полуоси, координаты фокусов и эксцентриситет.
3. Составить уравнение параболы с вершиной (-1; 1) и фокусом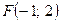 
.
4. Определить вид кривых второго порядка , их параметры. Построить кривые
а)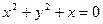 
;
б)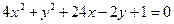 
;
в)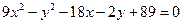 
;
г)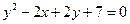 
Ответы
2. 
, 
, 
, 
, 
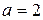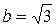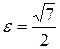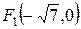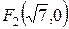
1. 
.
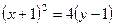Полярная система координат
Пример 1. Построить в полярной системе координат точки:
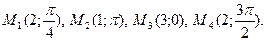
Решение.
|
|
|
|
|
|
 |
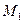
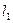
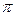
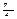
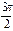
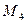
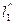
Пример 2.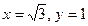 
- координаты точки М. Найти полярные координаты точки М.
Решение.
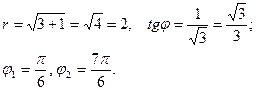
Равенства (4.25) примут вид: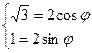 
Отсюда имеем:
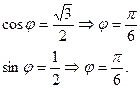
Таким образом, полярные координаты точки М равны: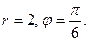 
Пример 3.. Дано полярное уравнение линии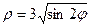 
. Построить эту линию по точкам. Найти ее декартово уравнение.
Решение. Выражение в правой части имеет смысл при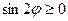 
, то есть 
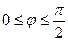и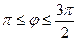 
. Учитывая периодичность функции (период Т= 
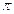) достаточно рассмотреть 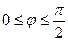. Составим таблицу значений функции, ограничиваясь точностью 0,01:
 |  |  |  |  |  |  | |
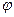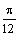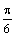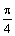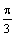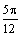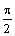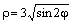 | 2,12 | 2,79 | 2,79 | 2,12 |
Проведем лучи, соответствующие выбранным значениям 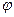, и на каждом из них отложим вычисленное значение 
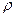. Полученные точки соединим плавной кривой (см. рис. ниже). Построенная линия называется лемнискатой Бернулли.
Чтобы перейти к декартовым координатам, запишем уравнение в виде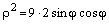 
и воспользуемся формулами (4.26, 4.28):
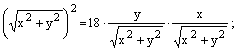
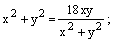
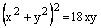
– уравнение линии в декартовой системе координат.
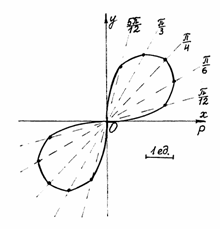
Рис.
Пример 4. Найти полярное уравнение окружности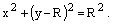 
Решение. Запишем уравнение в виде
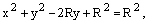или
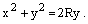
Воспользуемся формулами (4.25):
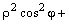
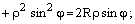
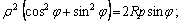
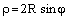– искомое уравнение.