Кривые второго порядка на плоскости
Уравнение вида Ах2+2Вху+Су2+2Dх+2Еу+F=0 называется общим уравнением кривой второго порядка. Коэффициенты уравнения – действительные числа, причем хотя бы одно из чисел А,В,С отлично от нуля. Такое уравнение определяет на плоскости окружность, эллипс, гиперболу или параболу.
В табл. 2 приведены уравнения кривых второго порядка и определен смысл входящих в них коэффициентов.
Таблица 2
| № п/п | Определение кривой | Вид уравнения | Примечание | |||||
 Эллипс – множество всех точек плоскости, сумма расстояний от которых до двух точек, называемых фокусами, есть величина постоянная (рис.4) Эллипс – множество всех точек плоскости, сумма расстояний от которых до двух точек, называемых фокусами, есть величина постоянная (рис.4) | 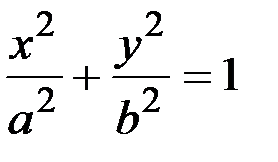 - каноническое уравнение эллипса - каноническое уравнение эллипса | 2а – большая ось; 2b – малая ось 2с–межфокус-ное расстояние с2=а2-b2; 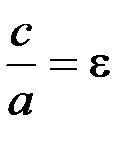 - эксцентриси-тет, 0<e<1. Т. А1,А2,В1,В2 – вершины эллипса - эксцентриси-тет, 0<e<1. Т. А1,А2,В1,В2 – вершины эллипса | ||||||
Гипербола – множество точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек, называемых фокусами, есть величина постоянная (рис.5) 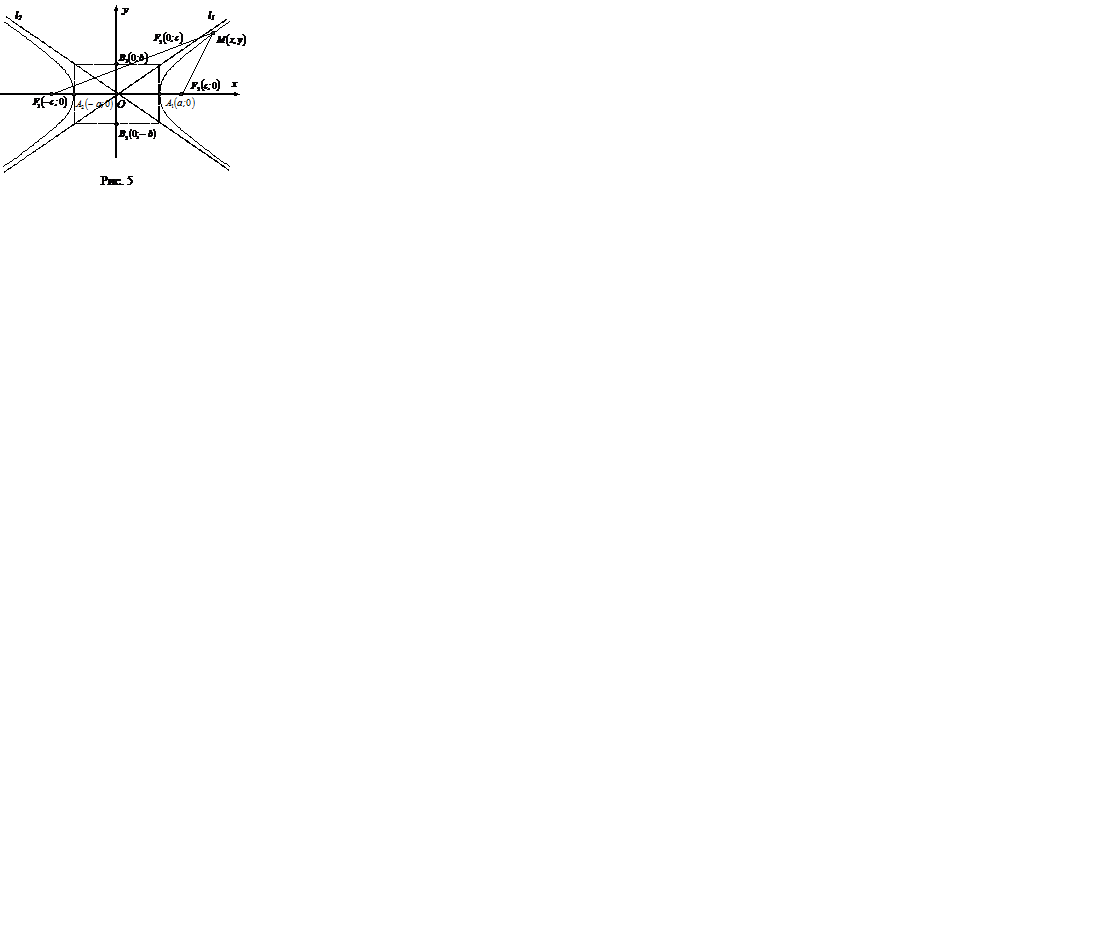 | 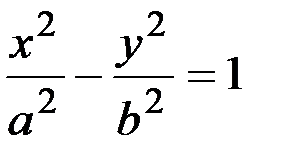 - каноническое уравнение гиперболы - каноническое уравнение гиперболы | 2а–действи-тельная ось; 2b–мнимая ось; 2с –меж-фокусное расстояние с2=а2+b2; 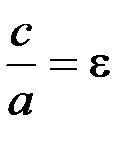 - эксцентри-ситет, e>1. Точки А1,А2 – вершины гиперболы. Прямые - эксцентри-ситет, e>1. Точки А1,А2 – вершины гиперболы. Прямые 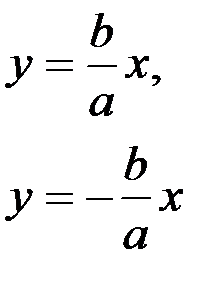 - асимптоты - асимптоты | ||||||
| 3. | Парабола - множество точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директриссой.
| у2=2px – каноническое уравнение параболы, симметричной относительно оси ОХ x2=2pу – каноническое уравнение параболы, симметричной относительно оси ОY (рис.6б) | F 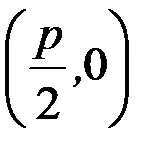 - фокус, - фокус, 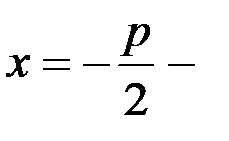 ди-ректриса. Точка (0;0) – вершина параболы (рис.6а) F ди-ректриса. Точка (0;0) – вершина параболы (рис.6а) F 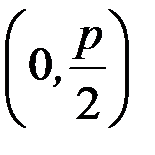 - фокус, - фокус, 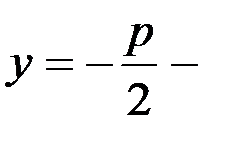 ди-ректриса. Точка (0;0) – вершина параболы (рис.6б) ди-ректриса. Точка (0;0) – вершина параболы (рис.6б) |
1. Найти координаты фокусов и эксцентриситет эллипса 36х2+100у2=3600.
Решение:
Приведем уравнение эллипса к каноническому виду:
36х2+100у2=3600, поделим обе части уравнения на 3600:
 , a2=100, b2=36.
, a2=100, b2=36.
Fл(-с,0) – левый фокус;
Fп(с,0) – правый фокус;
С= 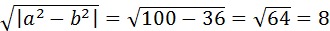 .
.
Fл(-8,0); Fп(8,0).
Эксцентриситет: 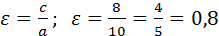 .
.
Ответ: Fл(-8,0); Fп(8,0); 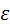 =0,8.
=0,8.
2.Написать уравнение прямой, проходящей через левую вершину эллипса 16х2+25у2=400 и точку М0(1;-3) (рис.7).
| у |
| -4 |
| -5 |
| М |
| х |
| М0 |
| Рис. 7 |
Приведем уравнение 16х2+25у2=400 к каноническому виду.
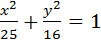 , a2=25, b2=16.
, a2=25, b2=16.
Левая вершина эллипса (-а,0)Þ(-5,0). Обозначим М(-5,0). Составим уравнение прямой, проходящей через точки М0 и М:
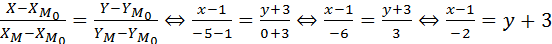 .
.
Ответ: 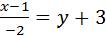 .
.
3. Написать уравнение прямой, проходящей через правый фокус гиперболы 9х2-16у2=144 и параллельно прямой 3х-2у+6=0 (рис.8).
Решение:
| -3 |
| -4 |
| FП |
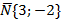 |
| х |
| у |
| Рис.8 |
Приведем уравнение 9х2-16у2=144 к каноническому виду 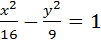 , a2=16, b2=9.
, a2=16, b2=9.
Правый фокус гиперболы Fп(с,0);
С= 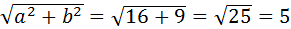 .
.
Итак, Fп(5,0).
1-й способ.
Условие параллельности двух прямых: k1=k2.
Пусть уравнение искомой прямой имеет вид y=k2x+b2;
3х-2у+6=0;
2у=3х+6;
у=(3/2)х+3;
k1=3/2Þk2=3/2.
Значит, y=(3/2)x+b2 проходит через точку Fп(5,0), то 0=(3/2)5+b2Þb2=-15/2. Итак, 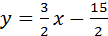 Û3x-2у-15=0.
Û3x-2у-15=0.
2-й способ.
Искомая прямая проходит через точку Fл(5,0) параллельно прямой 3х-2у+6=0. Из общего уравнения заданной прямой определяем вектор нормали 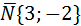 , который будет являться нормалью и для параллельной ей искомой прямой. Пользуемся уравнениемА(х-х0)+В(у-у0)=0, 3(х-5)-2(у-0)=0, 3х-2у-15=0.
, который будет являться нормалью и для параллельной ей искомой прямой. Пользуемся уравнениемА(х-х0)+В(у-у0)=0, 3(х-5)-2(у-0)=0, 3х-2у-15=0.
Ответ: 3х-2у-15=0.
4. Написать уравнение прямой l, проходящей через нижнюю вершину эллипса 4х2+20у2=80, перпендикулярно прямой 2х-у+1=0 (рис.9).
| М |
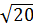 |
| -2 |
| y |
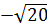 |
| l |
| х |
 |
| Рис. 9 |
Решение:
Приведем уравнение к каноническому виду 4х2+20у2=80,
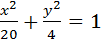 , a2=20, b2=4.
, a2=20, b2=4.
Нижняя вершина имеет вид: М(0;-b)=М(0;-2).
1-й способ.
Условие перпендикулярности двух прямых: k1k3=-1.
2х-у+1=0
у=2х+1Þk1=2.
Пусть уравнение прямой имеет вид: y=k2x+b2;
k2=-1: k1Þk2=-1/2, 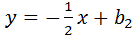
Так как прямая 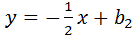 проходит через точку М(0;-2), то
проходит через точку М(0;-2), то 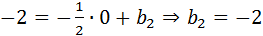 .
.
Итак, 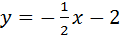 Þх+2у+4=0.
Þх+2у+4=0.
2-й способ.
По условию задачи требуется написать уравнение прямой l, проходящей через точку М(0;-2) перпендикулярно прямой 2х-у+1=0. Из общего уравнения прямой определяем координаты вектора нормали 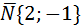 . Несложно представить (рис.9), что если искомая прямая l перпендикулярна заданной, то вектор
. Несложно представить (рис.9), что если искомая прямая l перпендикулярна заданной, то вектор 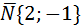 параллелен искомой прямой, т.е. является ее направляющим вектором. Используя уравнение прямой, проходящей через точку М0(х0,у0) параллельно вектору
параллелен искомой прямой, т.е. является ее направляющим вектором. Используя уравнение прямой, проходящей через точку М0(х0,у0) параллельно вектору 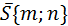 , получим:
, получим:
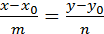 . У нас
. У нас 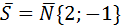 ;
; 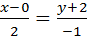 ;
;
-х=2у+4, х+2у+4=0.
Ответ: х+2у+4=0.
5. Написать уравнение прямой, проходящей через правый фокус эллипса 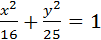 под углом 45˚ к оси Ох.
под углом 45˚ к оси Ох.
Решение:
a2=16, b2=25.
Правый фокус эллипса имеет вид Fп(с,0);
С= 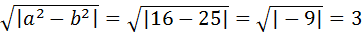 .
.
Итак, Fп(3,0).
Так как прямая проходит под углом 45˚ к оси Ох, то k=tgα=tg45˚=1.
Пусть уравнение искомой прямой имеет вид: y=kx+b;
k=1Þy=x+b.
Так как прямая проходит через точку Fп(3,0), то 0=3+bÞb=-3.
Значит, y=x-3.
Ответ: y=x-3.
Плоскость в пространстве
Любое уравнение первой степени в трехмерном пространстве определяет какую-либо плоскость.
Разным способам задания плоскости соответствуют различные виды уравнений (табл. 3.)
Таблица 3
| № п/п | Вид уравнения | Смысл входящих в уравнение коэффициентов | Примечание |
| Уравнение плоскости, проходящей через данную точку перпендикулярно заданному вектору А(х-х0)+В(у-у0)+С(z-z0)=0 | (x0,y0,z0) – координаты заданной точки; АВС – координаты заданного вектора | Вектор N(А,В,С) называется нормальным вектором плоскости | |
| Общее уравнение плоскости Ах+Ву+Сz+D=0 | D=-Ax0-By0-Cz0, АВС – нормальный вектор плоскости; | Это уравнение получается из уравнения (1) эле-ментарными | |
| № п/п | Вид уравнения | Смысл входящих в уравнение коэффициентов | Примечание |
| х0,y0,z0 – координаты данной точки | преобразованиями | ||
Уравнение плоскости, проходящей через три заданные точки 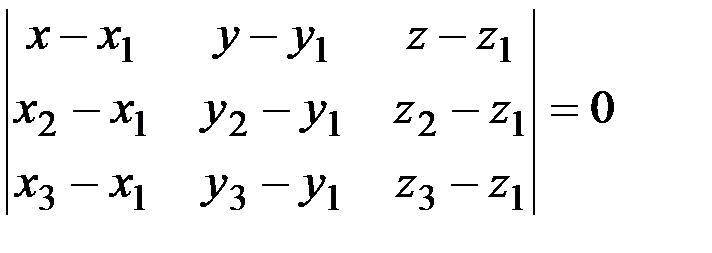 | М1(х1,y1,z1), М2(х2,y2,z2), М3(х3,y3,z3) – три точки, заданные своими координатами | Точки М1, М2, М3 не должны лежать на одной прямой | |
Уравнение плоскости в отрезках на осях 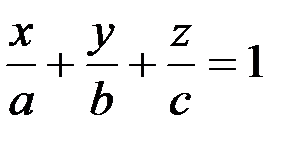 | а,b,c – отрезки, отсекаемые плоскостью от осей координат | аbc≠0 |
Пусть даны две плоскости a1 и a2:
a1: А1х +В1у+С1z+D1=0,
a2: А2х +В2у+С2z+D2=0.
Угол между двумя плоскостями определяется как 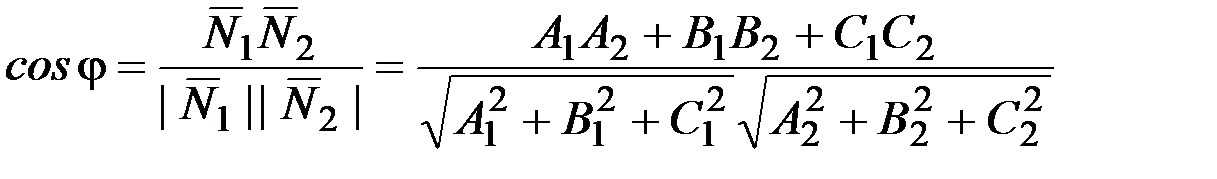 .
.
Условие перпендикулярности двух плоскостей:
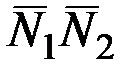 =0, то есть
=0, то есть 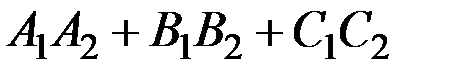 =0.
=0.
Условие параллельности двух плоскостей:
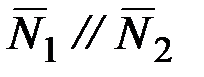 или
или 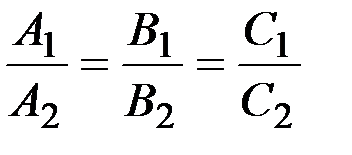 .
.
Расстояние от точки до плоскости:
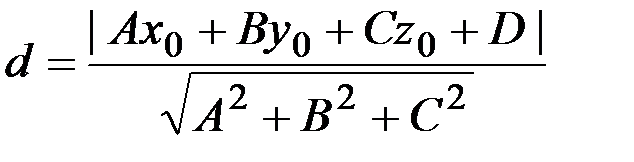 ,
,
где Ах+Ву+Сz+D=0 – заданная плоскость; М(x0,y0,z0) – данная точка.
Примеры решения типовых задач
1. Написать уравнение плоскости, проходящей через точку М(-1;1,3) перпендикулярно вектору 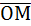 .
.
Решение:
Найдем координаты вектора 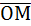 : О(0;0;0); М(-1;1;3) Þ
: О(0;0;0); М(-1;1;3) Þ
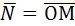 {-1;1;3}.
{-1;1;3}.
Уравнение плоскости имеет вид:
A(x-x0)+B(y-y0)+C(z-z0)=0
А=-1, В=1, С=3 – координаты вектора нормали.
X0=-1, y0=1, z0=3.
-1(х+1)+1(у-1)+3(z-3)=0
-х-1+у-1+3z-9=0
-х+у+3z-11=0.
Ответ: -х+у+3z-11=0.
2.Написать уравнение плоскости, проходящей через точки М1(1;-1;3), М2(2;-1;0), М3(4;2;-1).
Решение:
Уравнение плоскости, проходящей через три точки имеет вид:
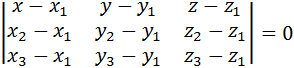 ,
,
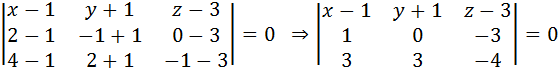
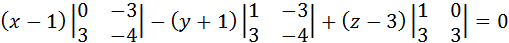 ,
,
9(х-1)-5(у+1)+3(z-3)=0
9х-9-5у-5+3z-9=0
9х-5у+3z-23=0.
Ответ: 9х-5у+3z-23=0.
3. Написать уравнение плоскости, проходящей через точку М0(-2;7;3) параллельно плоскости х-4у+5z+1=0 (рис.10).
 {1;-4;5} {1;-4;5} |
| М0(-2;7;3) |
| Рис. 10 |
Решение:
Нормальный вектор для плоскости х-4у+5z+1=0  {1;-4;5} является нормальным для искомой плоскости. Так как плоскость проходит через точку М0(-2;7;3), то уравнение плоскости имеет вид:
{1;-4;5} является нормальным для искомой плоскости. Так как плоскость проходит через точку М0(-2;7;3), то уравнение плоскости имеет вид:
A(x-x0)+B(y-y0)+C(z-z0)=0;
1(х+2)-4(у-7)+5(z-3)=0;
х+2-4у+28+5z-15=0;
х-4у+5z+15=0.
Ответ: х-4у+5z+15=0.
4. Найти расстояние от точки М0(1;-1;3) до плоскости 13х+2у- -5z+1=0.
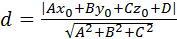 ; х0=1; у0=-1; z0=3.
; х0=1; у0=-1; z0=3.
А=13; В=2; С=-5, D=1.
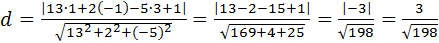 .
.
Ответ: d= 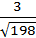 .
.
5. Найти угол между плоскостями х+у-1=0 и 2х-у+3z-1=0.
Решение:
Угол между плоскостями определяем как угол между нормалями к этим плоскостям. Из общих уравнений плоскостей определяем координаты нормалей 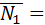 {1;1;0},
{1;1;0}, 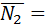 {2;-1;3}.
{2;-1;3}.
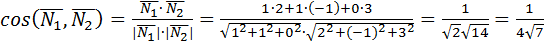 .
.
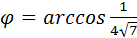 .
.
Ответ: 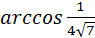 .
.
Прямая в пространстве.
Прямая и плоскость
Различным способам задания прямой в пространстве соответствуют разные виды ее уравнений, основные из которых представлены в табл. 4.
Таблица 4
| № п/п | Вид уравнения | Смысл входящих в уравнение коэффициентов | Примечание |
Канонические уравнения прямой 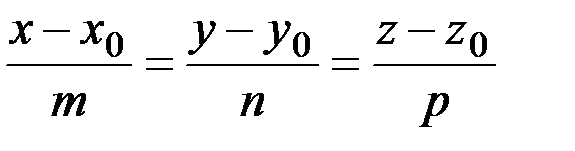 | (x0,y0,z0) – координаты точки М0, лежащей на прямой; m,n,p – координаты вектора, параллельного прямой | Вектор 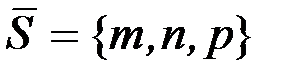 называется направля-ющим вектором прямой называется направля-ющим вектором прямой | |
Уравнение прямой, проходящей через две заданные точки 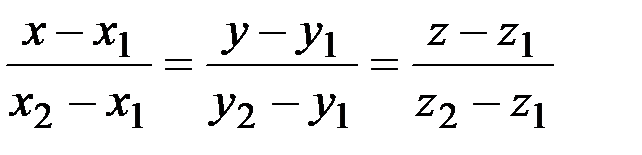 | (x1,y1,z1), (x2,y2,z2) – координаты двух заданных точек | Уравнение является обобще-нием уравнения прямой на плоскости | |
Уравнения прямой как линии пересечения двух плоскостей 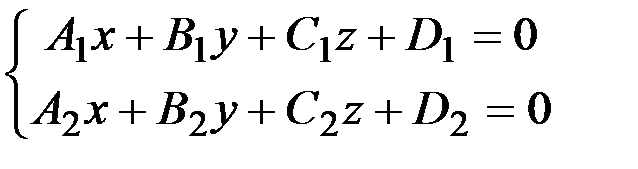 | 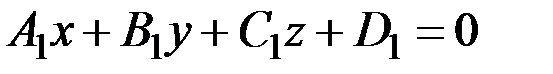 - уравнение одной плоскости; - уравнение одной плоскости; 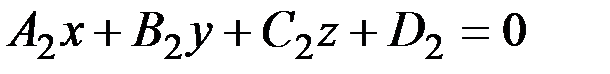 - уравнение второй плоскости - уравнение второй плоскости | Уравнения иначе назы-ваются общими уравне-ниями прямой в простран-стве |
Пусть заданы две прямые своими каноническими уравнениями:
l1: 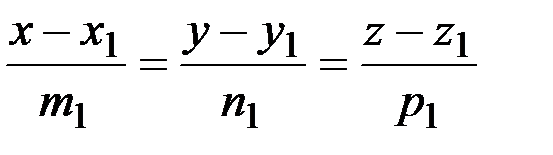
l2: 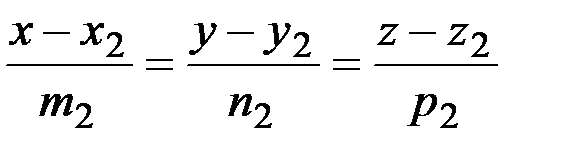 .
.
Угол между прямыми определяется как 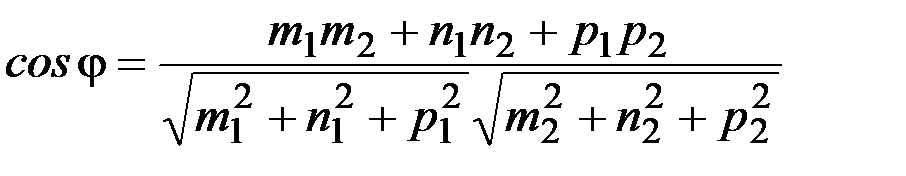 .
.
Условие перпендикулярности прямых:
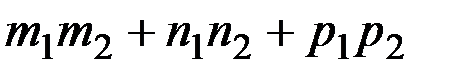 =0.
=0.
Условие параллельности прямых:
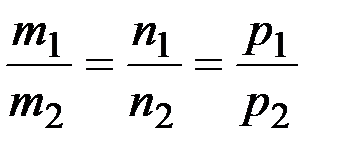 .
.
Пусть плоскость a задана уравнением Ах+Ву+Сz+D=0, а прямая l – своими каноническими уравнениями 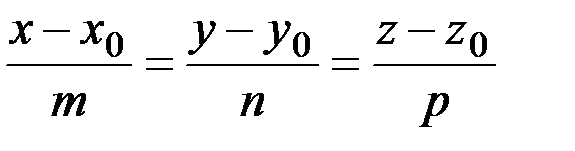 , тогда угол между прямой и плоскостью определяется как
, тогда угол между прямой и плоскостью определяется как
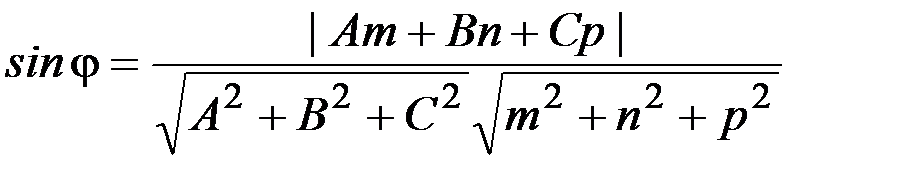 .
.
Условие параллельности прямой и плоскости Аm+Bn+Cp=0.
Условие перпендикулярности прямой и плоскости:
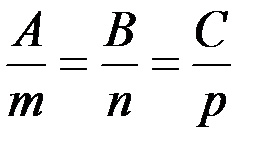 .
.
Примеры решения типовых задач
1. Написать уравнение плоскости, проходящей через точку М(2,4,-3) перпендикулярно прямой 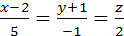 (рис.11).
(рис.11).
Решение:
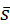 {5;-1;2} {5;-1;2} |
| М(2;4;-3) |
| Рис. 11 |
Чтобы написать уравнение плоскости A(x-x0)+B(y-y0)+C(z-z0)=0, необходимо знать координаты любой точки, лежащей в плоскости (у нас это точка М(2;4;-3)), и координаты вектора, перпендикулярного плоскости. Так как прямая 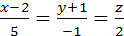 перпендикулярна плоскости, то ее направляющий вектор
перпендикулярна плоскости, то ее направляющий вектор 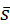 {5;-1;2} можно взять в качестве вектора-нормали к плоскости. Теперь запишем уравнение искомой плоскости:
{5;-1;2} можно взять в качестве вектора-нормали к плоскости. Теперь запишем уравнение искомой плоскости:
5(х-2)-1(у-4)+2(z+3)=0;
5х-10-у+4+2z+6=0;
5х-у+2z=0.
Ответ: 5х-у+2z=0.
2. Написать канонические уравнения прямой, проходящей через точку М(2;4;-3) перпендикулярно плоскости 3х-2у+5z-1=0 (рис.12).
Решение:
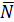 {-3;-2;5} {-3;-2;5} |
| М(2;4;-3) |
| Рис.12 |
Чтобы написать канонические уравнения прямой в пространстве 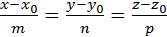 , необходимо знать координаты любой точки М(х0,у0,z0), через которую проходит прямая (у нас эта точка М(2;4;-3)), и координаты направляющего вектора
, необходимо знать координаты любой точки М(х0,у0,z0), через которую проходит прямая (у нас эта точка М(2;4;-3)), и координаты направляющего вектора 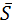 {m;n;p}(вектора, параллельного прямой). Так как прямая перпендикулярна плоскости, то она параллельна вектору нормали к плоскости. Следовательно, определив из уравнения плоскости координаты вектора нормали
{m;n;p}(вектора, параллельного прямой). Так как прямая перпендикулярна плоскости, то она параллельна вектору нормали к плоскости. Следовательно, определив из уравнения плоскости координаты вектора нормали 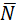 {-3;-2;5}, возьмем его в качестве направляющего вектора прямой. Теперь запишем каноническое уравнение искомой прямой
{-3;-2;5}, возьмем его в качестве направляющего вектора прямой. Теперь запишем каноническое уравнение искомой прямой
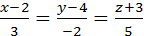 .
.
Ответ: 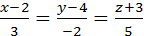 .
.
3. Написать уравнения прямой, проходящей через точку М0(2;-3;-4) параллельно прямой 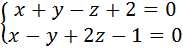 .
.
Решение:
Уравнение прямой будем искать в виде 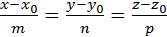 , где
, где
x0,y0,z0 – координаты точки, через которую проходит прямая (у нас это точка М0(2;-3;-4)), 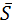 {m;n;p} – направляющий вектор прямой. Так как искомая прямая параллельна заданной прямой, у них один и тот же направляющий вектор. Найдем направляющий вектор прямой, заданной в условии общими уравнениями. Общие уравнения прямой задают, как линию пересечения двух плоскостей (рис.13).
{m;n;p} – направляющий вектор прямой. Так как искомая прямая параллельна заданной прямой, у них один и тот же направляющий вектор. Найдем направляющий вектор прямой, заданной в условии общими уравнениями. Общие уравнения прямой задают, как линию пересечения двух плоскостей (рис.13).
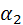 |
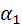 |
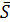 |
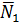 |
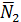 |
| М0(2;-3;-4) |
| Рис.13 |
Из общих уравнений плоскостей определяем координаты их нормалей 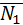 {1;1;-1} и
{1;1;-1} и 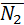 {1;-1;2}. Заметим, что направляющий вектор
{1;-1;2}. Заметим, что направляющий вектор 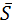 ^
^ 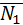 и
и 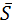 ^
^ 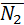 , следовательно, вектор
, следовательно, вектор 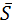 можно найти как векторное произведение
можно найти как векторное произведение 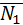 и
и 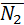 .
.
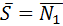 ´
´ 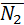 =
= 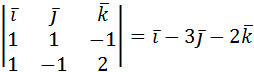 .
.
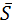 {1;-3;-2} – направляющий вектор искомой прямой. Тогда канонические уравнения прямой имеют вид:
{1;-3;-2} – направляющий вектор искомой прямой. Тогда канонические уравнения прямой имеют вид: 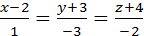 .
.
Ответ: 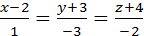 .
.
4. Написать уравнение плоскости, проходящей через пару параллельных прямых 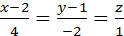 и
и 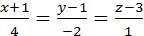 (рис. 14).
(рис. 14).
Решение:
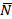 |
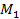 |
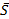 |
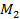 |
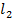 |
 |
| Рис.14 |
Чтобы написать уравнение плоскости в виде A(x-x0)+B(y-y0)+C(z-z0)=0, необходимо знать координаты любой точки М0(x0,y0,z0), лежащей в плоскости, и координаты вектора 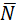 {А,В,С}, перпендикулярного плоскости.
{А,В,С}, перпендикулярного плоскости.
Из уравнений прямых определяем координаты точек М1(2;1;0) и М2(-1;1;3), лежащих на прямых, а следовательно, и в искомой плоскости. В качестве М0(x0,y0,z0) можем взять любую из них.
Теперь ищем вектор нормали. Заметим, что направляющий вектор прямых 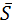 {4;-2;1} параллелен плоскости, а следовательно,
{4;-2;1} параллелен плоскости, а следовательно, 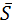 ^
^ 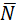 . Вектор
. Вектор 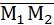 лежит в плоскости, следовательно,
лежит в плоскости, следовательно, 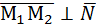 . Тогда
. Тогда 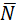 =
= 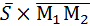 .
.
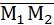 ={-1-2;1-1;3-0}={-3;0;3}.
={-1-2;1-1;3-0}={-3;0;3}.
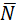 =
= 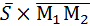 =
= 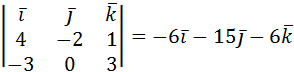 .
.
Итак, 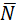 {-6;-15;-6} – нормальный вектор плоскости. Подставим координаты вектора и координаты любой из точек М1 или М2 в уравнение плоскости A(x-x0)+B(y-y0)+C(z-z0)=0, получим: -6(х-2)- -15(у-1)-6(z-0)=0 (мы подставили точку М1(2;1;0)).
{-6;-15;-6} – нормальный вектор плоскости. Подставим координаты вектора и координаты любой из точек М1 или М2 в уравнение плоскости A(x-x0)+B(y-y0)+C(z-z0)=0, получим: -6(х-2)- -15(у-1)-6(z-0)=0 (мы подставили точку М1(2;1;0)).
2(х-2)+5(у-1)+2(z-0)=0;
2х-4+5у-5+2z=0;
2х+5у+2z-9=0.
Ответ: 2х+5у+2z-9=0.
5. Написать уравнение плоскости, проходящей через точки М1(-1;0;2) и М2(3;2;1) перпендикулярно плоскости α: 2х-3у+z-5=0.
Решение:
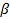 |
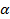 |
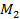 |
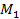 |
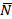 |
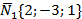 |
| Рис.15 |
Ищем уравнение плоскости β в виде A(x-x0)+B(y-y0)+C(z-z0)=0 (рис.15). Нам необходимо иметь координаты любой точки, лежащей в плоскости (у нас их две М1 и М2), и координаты вектора нормали. Так как вектора нормали 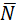 в условии задачи нет, следует найти любые два вектора, ортогональные нормали. Тогда их векторное произведение даст нам нормаль. На рис.15 видно, что
в условии задачи нет, следует найти любые два вектора, ортогональные нормали. Тогда их векторное произведение даст нам нормаль. На рис.15 видно, что 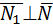 и
и 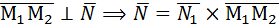 . Координаты вектора
. Координаты вектора 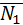 {2;-3;1}определяются из уравнения плоскости α. Найдем координаты вектора
{2;-3;1}определяются из уравнения плоскости α. Найдем координаты вектора 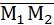 .
.
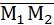 ={3-(-1);2-0;1-2}={4;2;-1}.
={3-(-1);2-0;1-2}={4;2;-1}.
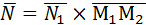 =
= 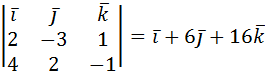 .
.
Подставляем координаты вектора 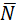 {1;6;16} и координаты любой из точек М1 и М2 (мы возьмем М1(-1;0;2)) в уравнение плоскости, получим:
{1;6;16} и координаты любой из точек М1 и М2 (мы возьмем М1(-1;0;2)) в уравнение плоскости, получим:
1(х+1)+6(у-0)+16(z-2)=0;
х+6у+16z-31=0;
Ответ: х+6у+16z-31=0.
6. Написать уравнение плоскости, проходящей через прямую 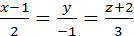 и точку М(2;3;-4).
и точку М(2;3;-4).
 |
| М1(1;0;-2) |
 |
| М(2;3;-4) |
| Рис.16 |
Чтобы написать уравнение плоскости A(x-x0)+B(y-y0)+C(z-z0)=0, необходимо знать координаты точки, лежащей в плоскости (у нас точка М(2;3;-4)), и координаты вектора нормали 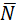 .
.
В условии задачи нет вектора нормали, но мы заметим (рис. 16), что направляющий вектор прямой 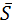 {2;-1;3}^
{2;-1;3}^ 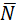 и вектор
и вектор 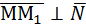 . Тогда
. Тогда 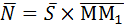 . Определив из уравнений прямой координаты точки М1(1;0;-2), найдем вектор
. Определив из уравнений прямой координаты точки М1(1;0;-2), найдем вектор 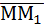 ={1-2;0-3;-2-(-4)}={-1;-3;2}.
={1-2;0-3;-2-(-4)}={-1;-3;2}.
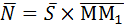 =
= 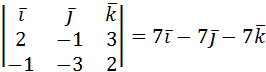 . Теперь запишем уравнение искомой плоскости:
. Теперь запишем уравнение искомой плоскости:
7(х-2)-7(у-3)-7(z+4)=0;
7х-14-7у+21-7z-28=0;
7х-7у-7z-21=0;
х-у-z-3=0.
Ответ: х-у-z-3=0.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Написать уравнение прямой, отсекающей на оси Оу отрезок b=3 и составляющей с осью Ох угол 45˚.
Ответ: у=-х+3.
2. Написать уравнение прямой, параллельной и перпендикулярной к прямой 2х+у+1=0 и проходящей через точку А(1;4).
Ответ: 2х+у-6=0, х-2у+7=0.
3. Найти расстояние от начала координат до прямой 6х+8у+20=0.
Ответ: 2.
4. Найти угол между прямыми у=2х-3 и 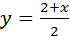 .
.
Ответ: arctg(2/4).
5. Написать каноническое уравнение эллипса, зная, что его большая полуось а=12, эксцентриситет равен 0,5. Найти расстояние между фокусами.
Ответ: 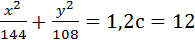 .
.
6. Написать каноническое уравнение гиперболы, зная, что: а) расстояние между фокусами равно 10, между вершинами равно 8; б) вещественная полуось равна 2Ö5, эксцентриситет равен Ö1,2.
Ответ: а) 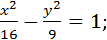 б)
б) 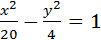 .
.
7. Написать уравнение плоскости, проходящей через точку М(-1;2;3) перпендикулярно вектору 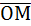 .
.
Ответ: х-2у-3z+14=0.
8. Написать уравнение плоскости, проходящей через точки М1(3;-1;2), М2(4;-1;-1), М3(2;0;2).
Ответ: 3х+3у+z-8=0.
9. Найти угол между плоскостями х+у-1=0 и 2х-у+ 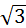 z+1=0.
z+1=0.
Ответ: arcos(1/4).
10. Найти расстояние от точки М(2;-1;-1) до плоскости 16х+12у+15z-4=0.
Ответ: 1.
11. Найти уравнение плоскости, проходящей через прямую 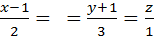 перпендикулярно плоскости 3х+3у-z+1=0.
перпендикулярно плоскости 3х+3у-z+1=0.
Ответ: 6х-5у+3z-11=0.
12. Написать уравнение прямой, проходящей через точки А(-1,2,3) и В(2,6,-2).
Ответ: 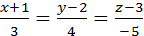 .
.
13. Написать уравнение прямой, проходящей через точку (-4;3;0) параллельно прямой 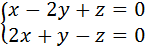 .
.
Ответ: 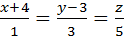 .
.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Основная
1. Письменный, Д.Т. Конспект лекций по высшей математике/ Д.Т. Письменный. – 6-е изд. М.: Айрис-пресс, 2006.-288с.
2. Минорский, В.П. Сборник задач по высшей математике: учеб. пособ. для втузов/ В.П. Минорский. – М.: Физматлит., 2004.
Дополнительная
1. Данко, П.Е. Высшая математика в упражнениях и задачах/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Оникс 21 век: Мир и образование, 2005. – 242с.
2. Лунку, К.Н. Сборник задач по высшей математике/ К.Е. Лунку. – М.: Айрис-пресс, 2009. – 592с.
Высшая математика. Векторная алгебра. Аналитическая геометрия: методические указания и примеры решения типовых задач для студентов I курса очной формы обучения инженерно-технических направлений (I семестр)
Ольшевская Наталия Андреевна
Цуленева Галина Георгиевна
Сенько Ксения Александровна
Научный редактор А.И.Гореленков
Редактор издательства Л.И. Афонина
Компьютерный набор А.П. Левкина
Темплан. 2012г,п. 59
Подписано в печать Формат 60´84 1/16. Бумага офсетная. Печать офсетная. Печ. л. 2,9 Уч.-изд. л. 2,9 Т. 40экз. Заказ бесплатно
Брянский государственный технический университет
241035, г. Брянск, бульвар им. 50-летия Октября, 7, БГТУ, 58-82-49.
Лаборатория оперативной полиграфии БГТУ, ул. Институтская, 16.