Задача СП.6. Пряма задача розходження суден
Судно А йде курсом 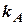 з абсолютним значенням швидкості
з абсолютним значенням швидкості 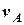 . За допомогою його радіолокаційної апаратури встановлено, що на момент часу t = 0 пеленг іншого судна В становить
. За допомогою його радіолокаційної апаратури встановлено, що на момент часу t = 0 пеленг іншого судна В становить 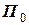 та відстань до нього
та відстань до нього 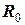 і воно рухається курсом
і воно рухається курсом 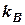 з абсолютним значенням швидкості
з абсолютним значенням швидкості 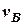 . В області руху суден течія відсутня.
. В області руху суден течія відсутня.
Визначити схему розходження суден. Визначити мінімальну відстань між судами (dкр) при розходженні та проміжок часу (tкр), через який це відбудеться. Задачу розв’язати методом абсолютного та відносного рухів. При графічному методі дотримуватися масштабу: 1 см = 1 миля та 1 см = 2 вуз.
Дані взяти з таблиці СП.6.
Таблиця СП.6 – вихідні дані для виконання задачі СП.6
| № | 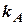 ,° ,° | 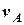 , вуз. , вуз. | 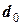 , миль , миль | 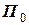 ,° ,° | 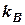 ,° ,° | 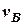 , вуз. , вуз. |
| 10,3 | ||||||
| 9,8 | 17,8 | |||||
| 13,2 | 8,5 | 11,8 | ||||
| 16,4 | 9,4 | 17,6 | ||||
| 15,6 | 10,2 | 11,8 | ||||
| 11,2 | 14,6 | |||||
| 14,4 | 9,7 | 17,2 | ||||
| 15,2 | 10,3 | 16,4 | ||||
| 15,8 | 11,2 | 18,2 | ||||
| 8,4 | 14,2 | |||||
| 9,3 | ||||||
| 11,5 | ||||||
| 16,6 | 11,8 | |||||
| 10,5 | ||||||
| 10,2 | ||||||
| 8,3 | ||||||
| 11,5 | ||||||
| 11,8 | ||||||
| 14,2 | 18,4 | |||||
| 20,8 | 8,1 | |||||
| 9,6 | 11,2 | |||||
| 9,1 | ||||||
| 16,2 | 10,5 | |||||
| 11,3 |
Продовження таблиці СП.6
| № | 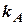 ,° ,° | 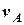 , вуз. , вуз. | 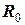 , миль , миль | 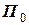 ,° ,° | 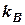 ,° ,° | 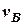 , вуз. , вуз. |
| 9,6 | ||||||
| 9,8 | 15,6 | |||||
| 14,6 | 11,7 | 17,4 | ||||
| 14,8 | 8,3 | |||||
| 10,6 | 20,4 | |||||
| 16,4 | 16,2 |
Обернена задача розходження суден
Методика розв’язання оберненої задачі
Графічно. Вважаючи судно 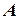 нерухомим, вказуємо положення судна
нерухомим, вказуємо положення судна 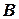 у початковий момент часу
у початковий момент часу 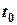 = 0 та у момент часу
= 0 та у момент часу 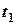 =0,1 год. = 6 хв.. Визначаємо відносне переміщення судна В і будуємо лінію відносного руху.
=0,1 год. = 6 хв.. Визначаємо відносне переміщення судна В і будуємо лінію відносного руху.
Визначаємо вектор швидкості 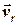 судна В відносно судна А.
судна В відносно судна А.
Знаходимо мінімальну відстань між суднами 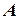 та
та 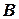 і обчислюємо момент часу
і обчислюємо момент часу 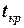 , коли це відбувається.
, коли це відбувається.
Будуємо абсолютну швидкість 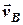 судна
судна 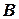 як суму векторів
як суму векторів 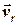 і
і 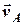 та вимірюємо його величину та напрям.
та вимірюємо його величину та напрям.
Будуємо схему абсолютного руху суден. Знаходимо шлях, який проходить кожне судно на момент розходження і вказуємо положення суден на цій схемі.
Аналітично – вводимо декартову систему координат, початок якої знаходиться у положенні судна 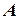 . Записуємо вирази для координат відносного положення судна
. Записуємо вирази для координат відносного положення судна 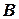 у моменти часу
у моменти часу 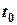 = 0 та
= 0 та 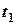 =0,1 год.
=0,1 год.
Розраховуємо вектор відносної швидкості 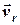 що дозволяє знайти найкоротшу відстань при розходженні та момент розходження.
що дозволяє знайти найкоротшу відстань при розходженні та момент розходження.
Записуємо вираз для вектора швидкості судна 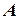
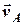 і знаходимо вектор абсолютної швидкості судна
і знаходимо вектор абсолютної швидкості судна 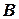
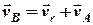 ,
,
знаходимо його модуль 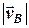 та курс
та курс 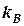 .
.
Визначаємо шлях, який проходить кожне судно на момент розходження і .
Приклад. Судно 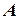 рухається курсом
рухається курсом 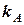 = 42° зі швидкістю
= 42° зі швидкістю 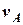 = 24 вузла. З судна
= 24 вузла. З судна 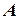 , на якому знаходиться спостерігач, за допомогою навігаційної апаратури встановлено, що у початковий момент часу
, на якому знаходиться спостерігач, за допомогою навігаційної апаратури встановлено, що у початковий момент часу 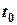 = 0 пеленг на корабель
= 0 пеленг на корабель 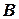 складав
складав 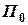 = 120°, а відстань (дистанція) до нього
= 120°, а відстань (дистанція) до нього 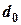 =12,8 миль, а у момент часу
=12,8 миль, а у момент часу 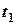 =0,1 год = 6 хв. вказані величини отримали значення
=0,1 год = 6 хв. вказані величини отримали значення 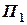 = 126° та
= 126° та 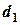 =9,6 миль. Вважаючи кожне судно матеріальною точкою, знайти:
=9,6 миль. Вважаючи кожне судно матеріальною точкою, знайти:
1) Графічно мінімальну відстань між суднами 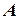 та
та 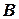 і момент часу
і момент часу 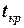 , коли це відбувається.
, коли це відбувається.
2) Графічно та аналітично швидкість 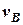 судна
судна 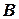 та його курс
та його курс 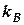 .
.
3) На схемі абсолютного руху суден 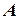 та
та 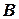 і вказати положення суден на момент часу
і вказати положення суден на момент часу 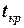 .
.
