Средства системы MATHCAD для моделирования на основе обыкновенных дифференциальных уравнений

В Mathcad имеются три встроенные функции, которые позволяют решать задачу Коши различными численными методами.

• rkfixed(y0, t0, t1, M, D) — метод Рунге-Кутты с фиксированным шагом,
• Rkadapt(y0, t0, t1, M, D) — метод Рунге-Кутты с переменным шагом;
• Buistoer(y0, t0, t1, M, D) — метод Булирша-Штера;
• у0 — вектор начальных значений в точке to размера NXI;
• t0 — начальная точка расчета,
• t1 — конечная точка расчета,
• M — число шагов, на которых численный метод находит решение;
• D — векторная функция размера NXI двух аргументов — скалярного t и векторного у При этом у — искомая векторная функция аргумента t того же размера NXI.

Соблюдайте регистр первой буквы рассматриваемых функций, поскольку это влияет на выбор алгоритма счета, в отличие от многих других встроенных функций Mathcad.

Каждая из приведенных функций выдает решение в виде матрицы размера (M+1)х(N+1). В ее левом столбце находятся значения аргумента t, делящие интервал на равномерные шаги, а в остальных N столбцах — значения искомых функций y₀(t) ,y₁(t), .. ,y_N-1(t), рассчитанные для этих значений аргумента. Поскольку всего точек (помимо начальной) М, то строк в матрице решения будет всего M+1

В подавляющем большинстве случаев достаточно использовать первую функцию rkfixed,

rkfixed(y,x1,x2,N,F) –выдает таблицу результатов решения системы обыкновенных дифференциальных уравнений методом Рунге-Кутта четвертого порядка точности с фиксированным шагом интегрирования :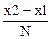

y – вектор начальных значений искомого решения;

x1 – начальное значение независимой переменной;

x2 – конечное значение независимой переменной;

N – фиксированное число шагов интегрирования на отрезке от х1 до х2: ;

F – правые части системы уравнений, записанные в символьном виде.

Пример использования функции rkfixed приведен ниже:

Результатом решения функции rkfixed является матрица. Первый столбец этой матрицы – это независимая переменная х с N=5 равномерными интервалами разбиения заданного отрезка х1-х2. Второй и так далее столбцы – это решения для соответствующих функций 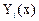с заданными начальными значениями.

Rkadapt(y,x1,x2,N,F) -выдает таблицу результатов решения системы обыкновенных дифференциальных уравнений методом Рунге-Кутта с адаптивным шагом интегрирования. Список параметров аналогичен функции rkfixed.

Пример использования функции Rkadapt приведен ниже.

Результирующая матрица имеет такой же вид, что и в функции rkfixed. Как видно, для одного итого же примера, приведенного для rkfixed и для Rkadapt решения немного расходятся. Следует ожидать, что решение по функции Rkadapt будет более точным.

Во-первых, функция D, входящая в число параметров встроенных функций для решения ОДУ, должна быть функцией обязательно двух аргументов. Во-вторых, второй ее аргумент должен быть вектором того же размера, что и сама функция D. В-третьих, точно такой же размер должен быть и у вектора начальных значений.

Не забывайте, что векторную функцию D(t,y) следует определять через компоненты вектора у с помощью кнопки нижнего индекса (Subscript) с наборной панели Calculator (Калькулятор) или нажатием клавиши <[>. В третьей строке листинга определено число шагов, на которых рассчитывается решение, а его последняя строка присваивает матричной переменной и результат действия функции rkfixed.

Чтобы построить график решения, надо отложить соответствующие компоненты матрицы решения по координатным осям" значения аргумента и<0> — вдоль оси х, а u<1> и u<2> — вдоль оси У .

При решении систем ОДУ многие проблемы могут быть устранены при помощи простой попытки увеличить число шагов численного метода В частности, сделайте так при неожиданном возникновении ошибки "Found a number with a magnitude greater than 10^307" (Найдено число, превышающее значение 10307) Данная ошибка может означать не то, что решение в действительности расходится, а просто недостаток шагов для корректной работы численного алгоритма

В заключение следует сказать несколько слов об особенностях различных численных методов. Все они основаны на аппроксимации дифференциальных уравнений разностными аналогами. В зависимости от конкретной формы аппроксимации, получаются алгоритмы различной точности и быстродействия. В Mathcad использован наиболее популярный алгоритм Рунге-Кутты четвертого порядка, описанный в большинстве книг по методам вычислений. Он обеспечивает малую погрешность для широкого класса систем ОДУ за исключением жестких систем. Поэтому в большинстве случаев стоит применять функцию rkfixed. Если по различным причинам время расчетов становится критичным или точность неудовлетворительна, стоит попробовать вместо rkfixed другие функции, благо сделать это очень просто, благодаря одинаковому набору параметров. Для этого нужно только поменять имя функции в программе.

Функция Rkadapt может быть полезна в случае, когда известно, что решение на рассматриваемом интервале меняется слабо, либо существуют участки медленных и быстрых его изменений. Метод Рунге-Кутты с переменным шагом разбивает интервал не на равномерные шаги, а более оптимальным способом. Там, где решение меняется слабо, шаги выбираются более редкими, а в областях его сильных изменений — частыми. В результате, для достижения одинаковой точности требуется меньшее число шагов, чем для rkf ixed. Метод Булирша-Штера Buistoer часто оказывается более эффективным для поиска гладких решений.

Задание 1. Стационарный режим, открытая СМО.

Задача 1 (По вариантам)

Имеется птелефонных линий. Вызов, пришедший в момент, когда все линии заняты, получает отказ. Интенсивность потока вызовов в минуту равна L. Средняя продолжи­тельность одного разговора равна t минут. Определить основные характеристики данной системы массового обслуживания в стационарном режиме.

ЗАМЕЧАНИЕ. Эта СМО без очереди, в отличие от рассмотренного ниже демонстрационного примера. Внимательно прочтите теорию!