Исследование функций и построение графиков
Целесообразно исследовать функцию по некоторой общей схеме, позволяющей последовательно изучить ее особенности. Можно рекомендовать такой порядок:
1. Найти область определения функции.
2. Исследовать функцию на четность и нечетность.
3. Найти точки пересечения графика функции с осями координат.
4. Исследовать функцию на непрерывность, найти (если они существуют) точки разрыва и установить характер разрыва; найти асимптоты кривой.
5. Найти интервалы возрастания и убывания функции и ее экстремумы.
6. Найти интервалы выпуклости и вогнутости кривой и точки ее перегиба.
Отметим, что иногда порядок исследования целесообразно выбирать, исходя из особенностей функции. Может быть пополнен и перечень исследуемых характеристик (например вопросом о периодичности функции).
Первые две позиции более подробно рассмотрены в разделе 1.1. Обсудим третью – Точки пересечения графика с осями координат.
Пусть функция задана соотношением 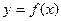 . Уравнения осей координат известны:
. Уравнения осей координат известны: 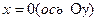 и
и 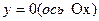 . Точки пересечения определятся как решения соответствующих систем уравнений:
. Точки пересечения определятся как решения соответствующих систем уравнений:
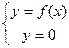 (с осью
(с осью 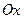 ) и
) и 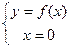 (с осью
(с осью 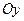 )
)
Пример 5.1. 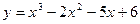
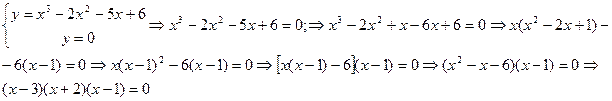
Т.е. график функции пересекает ось 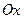 в точках
в точках 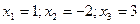 .
.
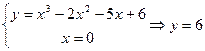 т.е. график пересекает ось
т.е. график пересекает ось 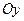 в точке
в точке 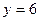 .
.
Непрерывность функции и характер точек разрыва рассмотрены в разделе 2. Напомним, что элементарная функция непрерывна во всей области определения. Т.е. исследовать нужно границы области D(f) и выколотые точки.
Пример 5.2. 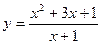 . Функция существует всюду, кроме точки
. Функция существует всюду, кроме точки 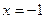 . Рассмотрим пределы
. Рассмотрим пределы
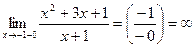 и
и 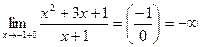 .
.
Т.о. 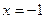 – точка разрыва 2-го рода (бесконечный разрыв).
– точка разрыва 2-го рода (бесконечный разрыв).
Обсудим проблему асимптот ( и убедимся в том, что 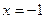 - уравнение вертикальной асимптоты).
- уравнение вертикальной асимптоты).
Асимптотой графика  называется прямая линия, обладающая тем свойством, что расстояние от переменной точки на графике до прямой стремится к нулю при неограниченном удалении этой точки по графику от начала координат.
называется прямая линия, обладающая тем свойством, что расстояние от переменной точки на графике до прямой стремится к нулю при неограниченном удалении этой точки по графику от начала координат.
Два вида асимптот – вертикальная и наклонная.
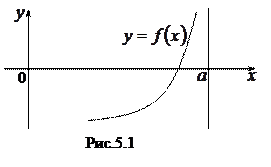 а) Вертикальной асимптотой кривой
а) Вертикальной асимптотой кривой 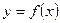 называется прямая
называется прямая 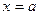 (рис. 5.1), если выполнено хотя бы одно условий:
(рис. 5.1), если выполнено хотя бы одно условий:
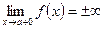 ; (5.1) или
; (5.1) или 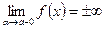 . (5.2)
. (5.2)
Для отыскания вертикальной асимптоты графика функции 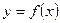 надо найти те значения
надо найти те значения 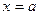 , при которых функция обращается в бесконечность. Тогда вертикальная асимптота имеет уравнение
, при которых функция обращается в бесконечность. Тогда вертикальная асимптота имеет уравнение 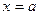 .
.
б) Наклонной асимптотой кривой 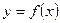 называется прямая (рис 5.2), имеющая уравнение
называется прямая (рис 5.2), имеющая уравнение 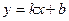 , если параметры
, если параметры 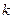 и
и 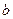 находятся по формулам:
находятся по формулам:
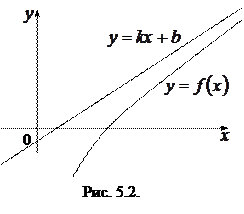
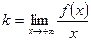 , (5.3) и
, (5.3) и 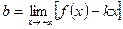 ,(5.4)
,(5.4)
Замечания:
1) Если хотя бы один из пределов не существует (или равен 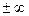 ), то график функции
), то график функции 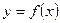 асимптоты при
асимптоты при 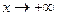 не имеет.
не имеет.
2) Частным случаем наклонной асимптоты при 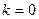 и
и 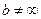 является горизонтальная асимптота (уравнение
является горизонтальная асимптота (уравнение 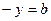 ).
).
3) Если 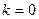 и
и 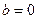 , то горизонтальной асимптотой является ось
, то горизонтальной асимптотой является ось 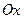 .
.
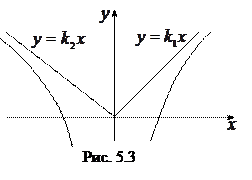 4) Аналогично находятся асимптоты при
4) Аналогично находятся асимптоты при 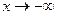 .
.
Заметим, что пределы (5.3) и (5.4) могут быть различными при 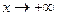 и
и 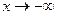 , т.е. график функции может иметь две различные наклонные асимптоты при
, т.е. график функции может иметь две различные наклонные асимптоты при 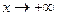 и
и 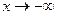 (рис. 5.3, где
(рис. 5.3, где 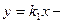 асимптоты при
асимптоты при 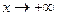 ,
, 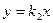 при
при 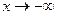 ).
).
Продолжим обсуждение примера 5.2. Очевидно, что 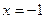 действительно уравнение вертикальной асимптоты. Проверим, существуют ли наклонные асимптоты. По формуле (5.3)
действительно уравнение вертикальной асимптоты. Проверим, существуют ли наклонные асимптоты. По формуле (5.3)
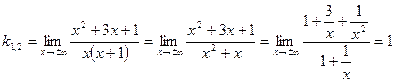
По формуле (5.4) 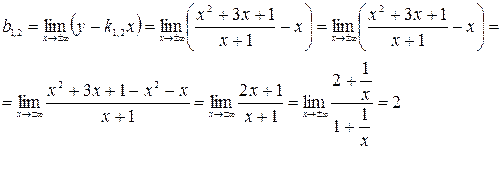
Прямая 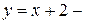 наклонная асимптота (при
наклонная асимптота (при 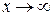 и
и 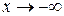 ) .
) .
Пример 5.3. 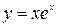
Функция 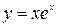 не имеет вертикальных асимптот, т.к. она всюду непрерывна (не имеет разрывов).
не имеет вертикальных асимптот, т.к. она всюду непрерывна (не имеет разрывов).
Наклонная: 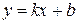 ,
, 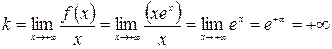 , т.е при
, т.е при 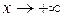 кривая не имеет наклонной асимптоты;
кривая не имеет наклонной асимптоты;
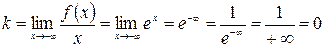
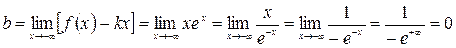
(применено правило Лопиталя).
Итак, прямая 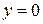 (ось
(ось 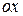 ) есть горизонтальная асимптота при
) есть горизонтальная асимптота при 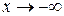 .
.
Интервалы монотонности (возрастания и убывания функции) и её экстремумы.
Функция 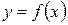 называется монотонно возрастающей на интервале
называется монотонно возрастающей на интервале 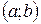 , если для любых
, если для любых 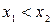 из этого интервала выполнено условие
из этого интервала выполнено условие
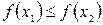 при
при 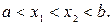
Функция 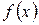 называется монотонно убывающей на интервале
называется монотонно убывающей на интервале 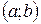 , если для любых
, если для любых 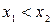 из этого интервала выполнено условие
из этого интервала выполнено условие
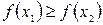 при
при 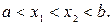
Дифференцируемая функция является монотонно возрастающей на интервале 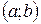 тогда и только тогда, когда
тогда и только тогда, когда 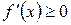 при
при 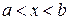 , (5.5)
, (5.5)
и является монотонно убывающей, если 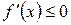 при
при 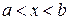 , (5.6)
, (5.6)
Условие (5.5) геометрически означает, что касательная к графику монотонно возрастающей функции образует с положительным направлением оси 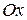 острый угол или параллельна ей. Касательная к графику монотонно убывающей функции образует тупой угол с положительным направлением оси
острый угол или параллельна ей. Касательная к графику монотонно убывающей функции образует тупой угол с положительным направлением оси 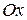 или параллельна ей.
или параллельна ей.
Экстремумы функции – максимум и минимум.
Функция 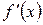 имеет максимум или минимум в точке
имеет максимум или минимум в точке 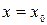 (локальный экстремум), если существует окрестность (
(локальный экстремум), если существует окрестность ( 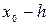 ;
; 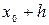 ), для всех точек которой выполнено условие
), для всех точек которой выполнено условие 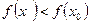 для максимума или
для максимума или 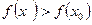 для минимума. Точка максимума или минимума называется точкой экстремума.
для минимума. Точка максимума или минимума называется точкой экстремума.
Точка 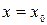 называется критической точкой первого рода, если:
называется критической точкой первого рода, если:
1) 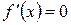 (касательная к графику параллельна оси
(касательная к графику параллельна оси 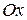 );
);
2) 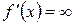 (касательная параллельна оси
(касательная параллельна оси 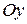 );
);
3) 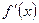 не существует (нет определенной касательной, например, как в угловой точке).
не существует (нет определенной касательной, например, как в угловой точке).
Наличие критической точки это необходимое условие экстремума.
Достаточным условием экстремума функции является перемена знака первой производной при переходе через критическую точку.
Отсюда правило исследования функции на экстремум:
1) Найти производную 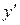 и критические точки, в которых
и критические точки, в которых 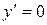 , или
, или 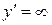 , или
, или 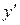 не существует, а сама функция непрерывна, и которые принадлежат области определения функции.
не существует, а сама функция непрерывна, и которые принадлежат области определения функции.
2) Определить знак 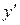 слева и справа от каждой критической точки.
слева и справа от каждой критической точки.
Если при переходе аргумента 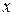 через критическую точку
через критическую точку 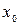 :
:
1) 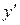 меняет знак с «+» на «-», то
меняет знак с «+» на «-», то 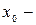 точка максимума;
точка максимума;
2) 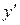 меняет знак с «-» на «+», то
меняет знак с «-» на «+», то 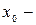 точка минимума;
точка минимума;
3) 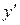 не меняет знак, то в точке
не меняет знак, то в точке 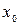 нет экстремума.
нет экстремума.
Далее следует найти экстремумы функции, т.е. вычислить значение функции в найденных точках экстремума.
Наибольшее и наименьшее значения функции на отрезке.
Для отыскания этих точек на отрезке 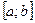 необходимо найти критические точки, принадлежащие этому отрезку и, вычислить значения функции в этих точках и на концах отрезка, выбрать наибольшее и наименьшее.
необходимо найти критические точки, принадлежащие этому отрезку и, вычислить значения функции в этих точках и на концах отрезка, выбрать наибольшее и наименьшее.
Пример 5.4. Определить интервалы монотонности функций:
1) 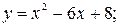 2)
2) 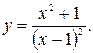
1) Данная функция всюду имеет производную
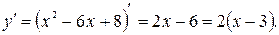
При 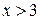 ,
, 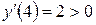 , поэтому, в силу условия (5.5), функция возрастает на интервале
, поэтому, в силу условия (5.5), функция возрастает на интервале 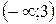 .
.
При 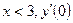 и, по условию (5.6) убывает на интервале
и, по условию (5.6) убывает на интервале 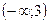
2) Функция 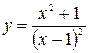 имеет производную всюду, кроме точки
имеет производную всюду, кроме точки 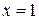 , в которой сама функция не определена. На каждом из интервалов
, в которой сама функция не определена. На каждом из интервалов 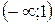 и
и 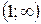 определим знаки производной
определим знаки производной 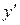 . Имеем
. Имеем
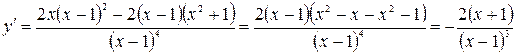 ,
,
Для определения знака 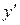 , выделим точки
, выделим точки 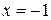 , в которой
, в которой 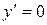 и
и 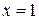 , в которой
, в которой 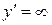 . Итак, имеем три интервала
. Итак, имеем три интервала 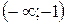 ,
, 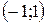 и
и 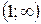 . На интервале
. На интервале 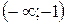 производная
производная 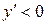 , на интервале
, на интервале 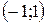
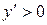 , на интервале
, на интервале 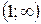
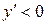 . Таким образом, функция убывает на интервалах
. Таким образом, функция убывает на интервалах 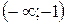 и
и 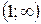 и возрастает на интервале
и возрастает на интервале 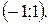
Пример 5.5. Найти точки экстремума функции: 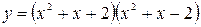
Функция 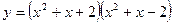 и её производная существует всюду, поэтому определим критические точки из условия
и её производная существует всюду, поэтому определим критические точки из условия 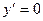 . Продифференцируем функцию как произведение двух функций:
. Продифференцируем функцию как произведение двух функций: 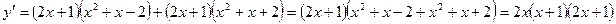 .
.
Из условия 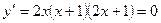 находим, приравнивая нулю каждый множитель отдельно, критические точки (необходимое условие экстремума):
находим, приравнивая нулю каждый множитель отдельно, критические точки (необходимое условие экстремума): 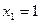 ;
; 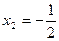 ;
; 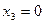 .
.
Исследуем критические точки, определяя знак 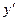 слева и справа от этой точки (первое достаточное условие экстремума). Для сокращения вычислений и для наглядности это исследование удобно записать в таблицу:
слева и справа от этой точки (первое достаточное условие экстремума). Для сокращения вычислений и для наглядности это исследование удобно записать в таблицу:
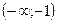 | 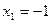 | 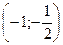 | 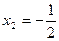 | 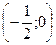 | 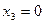 | 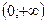 | |
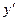 | - | + | - | + | |||
 |  Убыв. Убыв. |  min min |  Возр. Возр. |  max max |  Убыв. Убыв. |  min min |  Возр. Возр. |
В первой строчке помещены интервалы и критические точки в порядке расположения их на числовой оси. Во второй строке помещены знаки производной в промежутках между критическими точками. Например, берем 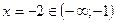 и находим
и находим 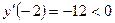 ,т.е.
,т.е. 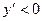 на интервале
на интервале 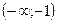 , аналогично
, аналогично 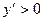 на интервале
на интервале 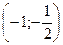 и
и 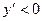 при
при 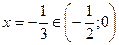 , и
, и 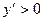 при
при 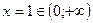 . В третьей строке – заключение о поведении функции. С использованием условий (5.7) получаем, что в точках
. В третьей строке – заключение о поведении функции. С использованием условий (5.7) получаем, что в точках 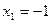 и
и 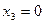 функция имеет минимум, а в точке
функция имеет минимум, а в точке 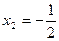 - максимум. Вычислим значения функции в этих точках:
- максимум. Вычислим значения функции в этих точках: 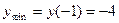 ;
; 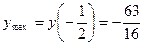 ,
, 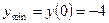 .
.
Пример 5.6. Найти наибольшее и наименьшее значения функции 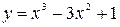 на отрезке
на отрезке 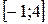 .
.
Найдем критические точки функции 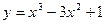 , лежащие внутри отрезка
, лежащие внутри отрезка 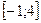 :
: 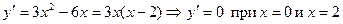 .
.
Эти точки лежат внутри отрезка 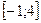 .
.
Вычислим значения функции на концах отрезка 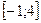 :
: 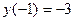 ,
, 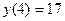 и в критических точках:
и в критических точках: 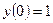 ,
, 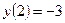 .
.
Сравнивая все вычисленные значения функции во внутренних критических точках и на концах отрезка, заключаем: наибольшее значение функции 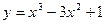 на отрезке
на отрезке 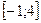
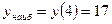 , а наименьшее
, а наименьшее 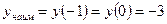 . Итак, наибольшее значение при
. Итак, наибольшее значение при 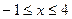 функция принимает на правом конце отрезка при
функция принимает на правом конце отрезка при 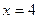 , а наименьшее значение достигается в двух точках, в точке минимума функции и на левой границе отрезка, при
, а наименьшее значение достигается в двух точках, в точке минимума функции и на левой границе отрезка, при 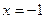 .
.
