Метод интегрирования по частям. Пусть u = u(x), v = v(x) – дифференцируемые функции

Пусть u = u(x), v = v(x) – дифференцируемые функции.

По свойству дифференциала 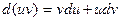или .

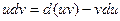Интегрируя обе части равенства, получим:

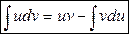- формула интегрирования по частям.

Метод заключается в следующем: подынтегральное выражение разбивается на 2 множителя u и dv. Далее, при переходе к правой части формулы, первый множитель дифференцируется, а второй – интегрируется: , .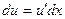

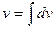Этот метод применяется для двух групп интегралов:

I. 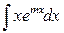; ; 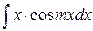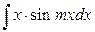(где m=const). В этой группе в качестве u выбирают х, а остальная часть подынтегрального выражения принимается за dv (u = x).

II. 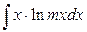; ; 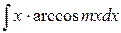; ; 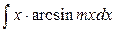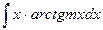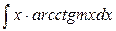(где m=const). В этой группе xdx = dv.

Пример 4. .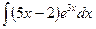

В нашем случае интеграл относится к I-ой группе интегралов, поэтому в качестве u возьмем 5х – 2 : u = 5х – 2, dv = e^3x∙dx.

= =

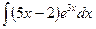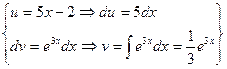(по формуле интегрирования по частям) = =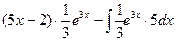

= .

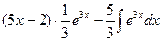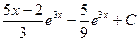Ответ: = .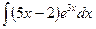

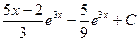Тема 4. Определённый интеграл

В.1 Формула Ньютона-Лейбница.

Пусть функция 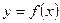непрерывна не отрезке 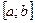и 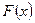любая первообразная функция на этом отрезке. Тогда определенный интеграл от функции 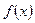на отрезке 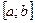равен приращению первообразной на данном отрезке.

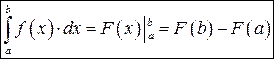
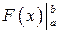- приращение первообразной на данном отрезке

То есть нахождение определенного интеграла с помощью формулы Ньютона-Лейбница осуществляется в два этапа:

1. Используя технику нахождения неопределенного интеграла находим первообразную подынтегральной функции.

2. Вычисляем приращение первообразной на заданном отрезке.

Пример 1: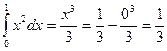

В.2. Замена переменной и интегрирование по частям

В определенном интеграле.

Метод замены переменной для определенного интеграла.

Пусть функция 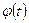имеет непрерывную производную на отрезке 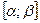, а также 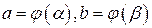и функция 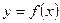непрерывна в любой точк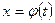е , где .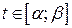

Тогда формула для замены переменной выглядит следующим образом:

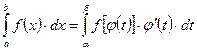
Замечание: в случае определенного интеграла нет необходимости возвращаться к исходной переменной интегрирования.

Пример 2: Вычислить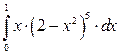

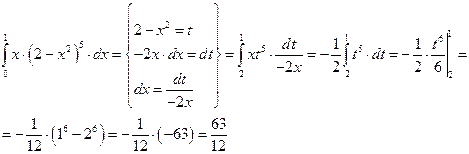
Метод интегрирования по частям для определенного интеграла

Пусть функция 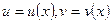имеет непрерывную производную на отрезке 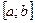, тогда формула интегрирования по частям:

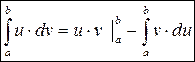
где 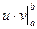- приращение: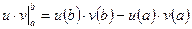

Тема 5. Обыкновенные дифференциальные уравнения (ОДУ)

В. 1. Основные понятия

Опр.: ОДУ называется уравнение вида: F(x, y, y’, y’’, …, y⁽ⁿ⁾) = 0, которое связывает искомую функцию одной переменной у = у(х), эту переменную и производные различных порядков искомой функции.

Наивысший порядок производной, входящей в запись уравнения, называется порядком уравнения.

ОДУ n-го порядка называется разрешенным относительно старшей производной, если оно имеет вид: у⁽ⁿ⁾ = f(x, y, y’, …, y^(n-1)).

Общим решением ОДУ n-го порядка называется функция у = φ(х, С₁, С₂, …, С_n) (где C_i – произвольные постоянные), которая обращает данное уравнение в тождество при подстановке в него этой функции и ее производных. Количество постоянных в решении совпадает с порядком уравнения.

Если общее решение уравнения будет получено в виде: Ф(х, у,С₁,С₂, …,С_n) = 0, то говорят, решение получено в виде общего интеграла уравнения.

Частные решения уравнения получаются из общего при конкретных значениях постоянных.

В.2. ОДУI

ОДУIв общем случае имеет вид: F(x, y, y’) = 0.

Разрешенное относительно производной: y’ = f(x, y)

или Р(х, у)dx + Q(x, y)dy = 0.

Опр.: Задача нахождения решения уравнения y’ = f(x, y), удовлетворяющего начальному условию y(x₀) = y₀, называется задачей Коши.

Общим решением ОДУI называется функция у = φ(х, С) (С = const), т. что:

1) она является решением уравнения при любом значении С;

2) для любого начального условия y(x₀) = y₀, существует С=С₀, т.что у = φ(х, С₀) удовлетворяет данному начальному условию.

Геометрически общее решение представляет собой семейство кривых на плоскости Оху, зависящее от С. Эти кривые называются интегральными кривыми данного ОДУI.