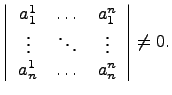
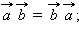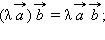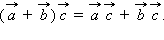Линейная зависимость и независимость векторов

Свойства арифметическогоn-мерного пространства

1. Ассоциативность

(a⃗ +b⃗ )+c⃗ =a⃗ +(b⃗ +c⃗ )(a→+b→)+c→=a→+(b→+c→).

2. Коммутативность

a⃗ +b⃗ =b⃗ +a⃗ a→+b→=b→+a→.

3. Единственность решения уравнения

∀a⃗ ,b⃗ ∃!x⃗ ∈Pⁿ(a⃗ +x⃗ =b⃗ ).

4. Существование нейтрального элемента

∃0⃗ =(0,0,0,…,0),∀a⃗ ,a⃗ +0⃗ =a⃗.

5. Существование противоположного вектора

∃0⃗ ,∀a⃗ ,a⃗ +0⃗ =a⃗ .

6. Ассоциативность скалярного умножения

∀λ,μ∈R :λ(μ⋅a⃗ )=(λ⋅μ)a⃗

7. Дистрибутивность умножения относительно сложения скаляров

(λ+μ)a⃗ =λa⃗ +μa⃗

8. Дистрибутивность умножения относительно сложения векторов

λ(a⃗ +b⃗ )=λa⃗ +λb⃗

Операции с векторами и их свойства

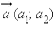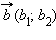Суммой векторов и называется

вектор 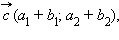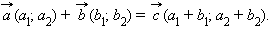Для любых векторов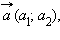 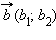справедливы равенства

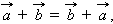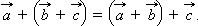Теорема 11.6.

Каковы бы ни были три точки A, B и C, имеет место векторное равенство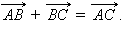

Правило параллелограмма: для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.

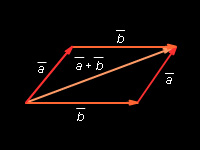Рисунок 11.2.3. Правило параллелограмма

Разностью векторов 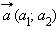и 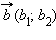называется такой вектор 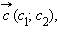который в сумме с вектором 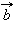дает вектор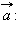 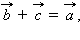откуда c₁ = a₁– b₁; c₂ = a₂– b₂.

Произведением вектора 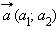на число λ называется вектор 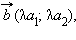т. е.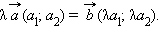

• Для любого вектора 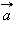и чисел λ и μ

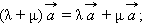• Для любых двух векторов 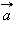и 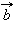и числа λ

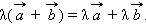Теорема 11.7.

Абсолютная величина вектора 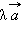равна |λ || a|. Направление вектора 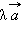при 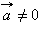совпадает с направлением вектора 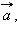если λ > 0, и противоположно направлению вектора 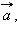если λ < 0.

Теорема 11.8.

Для любых отличных от нуля коллинеарных векторов 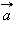и 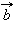существует такое число λ, что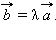

Теорема 11.9.

Пусть 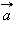и 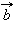– отличные от нуля неколлинеарные векторы. Любой вектор 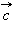можно единственным образом представить в виде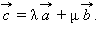

Скалярное произведение векторов.

Скалярным произведением векторов 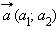и 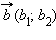называется число 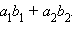Скалярное произведение векторов 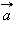и 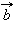обозначется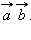

Для любых векторов 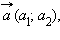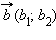и 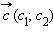верно:

• 
• 
• 

Теорема 11.10.

Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.

Единичные векторы 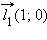и 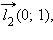имеющие направления положительных координатных полуосей, называются координатными векторами или ортами.

Теорема 11.11.

Любой ненулевой вектор 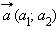единственным образом можно разложить по координатным векторам, то есть записать в виде .

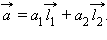Свойства умножения вектора на число:

1. 
2. 
3. 
4. 
5. 
6. .

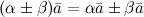
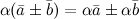
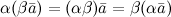
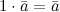
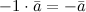
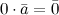Здесь 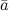и 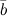- произвольные векторы, 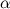, 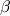- произвольные числа.

2. Определение 1. Система векторов 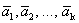называется линейно зависимой, если один из векторов системы можно представить в виде линейной комбинации остальных векторов системы, и линейно независимой - в противном случае.

Определение 1´. Система векторов 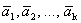называется линейно зависимой, если найдутся числа с₁, с₂, …, с_k, не все равные нулю, такие, что линейная комбинация векторов с данными коэффициентами равна нулевому вектору: 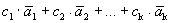= 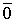, в противном случае система называется линейно независимой.

Покажем, что эти определения эквивалентны.

Пусть выполняется определение 1, т.е. один из векторов системы равен линейной комбинации остальных:

,

.

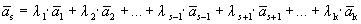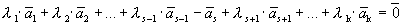Линейная комбинация системы векторов равна нулевому вектору, причем не все коэффициенты этой комбинации равны нулю, т.е. выполняется определение 1´.

Пусть выполняется определение 1´. Линейная комбинация системы векторов равна 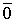, причем не все коэффициенты комбинации равны нулю, например, коэффициенты при векторе .

,

,

.

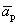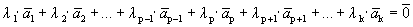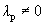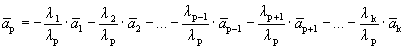Один из векторов системы мы представили в виде линейной комбинации остальных, т.е. выполняется определение 1.

Определение 2. Единичным вектором, или ортом, 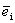называется n-мерный вектор, у которого i-я координата равна единице, а остальные - нулевые.

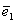. (1, 0, 0, …, 0),

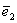(0, 1, 0, …, 0),

…

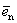(0, 0, 0, …, 1).

Теорема 1. Различные единичные векторы n-мерного пространства линейно независимы.

Доказательство. Пусть линейная комбинация этих векторов с произвольными коэффициентами равна нулевому вектору.

= .

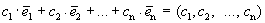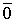Из этого равенства следует, что все коэффициенты равны нулю. Получили противоречие.

Каждый вектор n-мерного пространства ā(а₁, а₂ , ..., а_n) может быть представлен в виде линейной комбинации единичных векторов с коэффициентами, равными координатам вектора

.

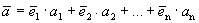Теорема 2. Если системы векторов содержит нулевой вектор, то она линейно зависима.

Доказательство. Пусть дана система векторов 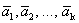и один из векторов является нулевым, например 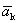= 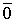. Тогда с векторами данной системы можно составить линейную комбинацию, равную нулевому вектору, причем не все коэффициенты будут нулевыми:

= .

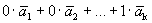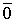Следовательно, система линейно зависима.

Теорема 3. Если некоторая подсистема системы векторов линейно зависима, то и вся система линейно зависима.

Доказательство. Дана система векторов 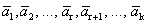. Предположим, что система 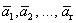линейно зависима, т.е. найдутся числа с₁, с₂, …, с_r, не все равные нулю, такие, что 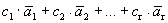= 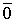. Тогда

= .

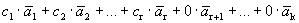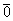Получилось, что линейная комбинация векторов всей системы равна 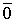, причем не все коэффициенты этой комбинации равны нулю. Следовательно, система векторов линейно зависима.

Следствие. Если система векторов линейно независима, то и любая ее подсистема также линейно независима.

Доказательство.

Предположим противное, т.е. некоторая подсистема линейно зависима. Из теоремы следует, что вся система линейно зависима. Мы пришли к противоречию.

Теорема 4 (теорема Штейница).Если каждый из векторов 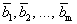является линейной комбинацией векторов 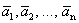и m>n, то система векторов 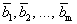линейно зависима.

Следствие. В любой системе n-мерных векторов не может быть больше чем n линейно независимых.

Доказательство. Каждый n-мерный вектор выражается в виде линейной комбинации n единичных векторов. Поэтому, если система содержит m векторов и m>n, то, по теореме, данная система линейно зависима.

Линейная зависимость и независимость векторов

Система 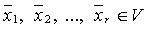линейно зависима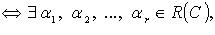 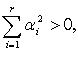что

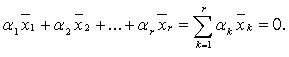
Система 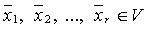линейно независима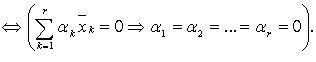

Критерий линейной зависимости векторов

Для того чтобы векторы 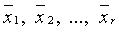(r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных.

Лемма.

Пусть система векторов 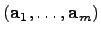линейно независима, а каждый ее вектор линейно выражается через векторы системы 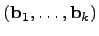. Тогда .

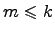Определение. Система 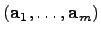называется максимальной линейно независимой системой в линейном пространстве 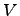, если любое расширение 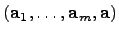этой системы линейно зависимо.

Следствие. Есл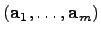и и 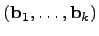две максимальные линейно независимые системы в 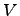, то .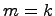

Определение. Пространство 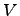называется 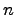-мерным ( 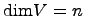), если в 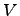есть максимальная линейно независимая система, состоящая из 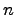векторов. Если такой подсистемы нет ни для каког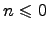о , то 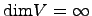. Если 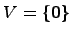, то по определению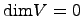

Определение. Система векторов 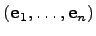называется базисом линейного пространства 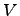, если каждый вектор 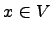единственным образом записывается в виде линейной комбинации , .

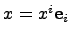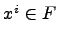Предложение. Система векторов 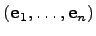является базисом в пространстве 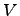тогда и только тогда, когда 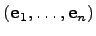является максимальной линейно независимой системой в .

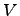Предложение. Пусть 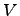-- -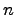мерное векторное пространство, 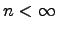. Тогда в 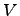существует хотя бы один базис. Более того, каждая линейно независимая система 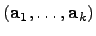может быть дополнена до некоторого базиса .

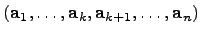Предложение. Система 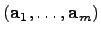является базисом в 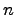-мерном векторном пространстве 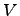тогда и только тогда, когда эта система линейно независима и .

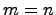Предложение. Система 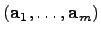является базисом в 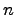-мерном векторном пространстве 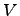тогда и только тогда, когда 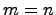и каждый вектор 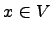линейно выражается через эти векторы.

Рассмотрим арифметическое пространство 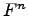, состоящее из множества строк 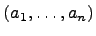, 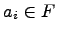. Вектор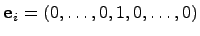а (на 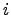месте стоит 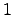) -- образуют базис.

Следствие. В пространстве 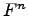система 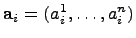, , 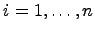является базисом тогда и только тогда, когда