Вейерштрасса(Th о достижении непрерывной на отрезке ф-ии своих точных граней)

Если f(x) непр. на [a,b], тогда она достигает своего экстр. на этом отрезке, т.е. $ т-ка max X*:f(x*)³f(x) "xÎ[a,b], т-ка min X_:f(x_)£f(x) "xÎ[a,b].

Док-во.Обозначим E(f) – множиством значений ф-ии f(x) на отр. [a,b] по предыд. т-ме это мн-во огран. и сл-но имеет конечные точные грани supE(f)=supf(x)=(при хÎ[a,b])=M(<¥). InfE(f)= inff(x)=m(m>-¥). Для опр. докажем [a,b] f(x) достигает макс. на [a,b], т.е. $ х*:f(x)=M. Допустим противное, такой т-ки не $ и сл-но f(x)<M "xÎ[a,b] рассмотрим вспомогат. ф-цию g(x)=1/(M-f(x) при хÎ[a,b]. g(x) – непр. как отношение 2-х непр. ф-ций и то знач. 0 согластно т-ме 1 g(x)- огран. т.е. $ c>0

!0<g(x)£c g³0, на [a,b] – 1/(M-f(x))£c => 1£c(M-f(x)) => f(x) £M-1/c "xÎ[a,b]

Однако это нер-во противор., т.к. М-точная верхн. грань f на [a,b] а в правой части стоит “C”

Теорема ВЕЙЕРШТРАССА. Эти теремы неверны если замкнутые отрезки заменить на др. пр-ки

Понятие производной

Пусть функция y=f(x) определена в некоторой окрестности точки x0. Пусть ▲x – приращение

аргумента в точке x0, а ▲y=f(x0+▲x)-f(x0)– соответствующее приращение функции. Составим

отношение ▲y/(поделить)▲x этих приращений и рассмотрим его предел при▲x->0. Если указанный

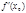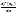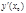предел существует, то он называется производной функции f в точке x0 и обозначается , или , то есть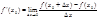

.

Операция вычисления производной называется дифференцированием, а функция, имеющая

производную в точке, – дифференцируемой в этой точке. Если функция имеет производную в

каждой точке интервала (a,b), то она называется дифференцируемой на этом интервале.

Геометрический смысл производной

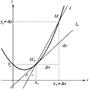а) Геометрический смысл производной. Рассмотрим график функции y=f(x), дифференцируемой в

точке x0 (рис. 13). Проведем через точки M0(x0,y0) и M(x0+▲x, y0+▲y) графика прямую l, и пусть

B(угол Бэтта) - угол ее наклона к оси х. Тогда (1)▲y/(деленный)▲x=tg B(бэтта)

Рис. 13.

Если ▲x стремится к нулю, то ▲y также стремится к нулю, и точка M приближается к точке M0, а

прямая l - к касательной l0(эль нулевая), образующей с осью x угол α(альфа). При этом

равенство (1) принимает вид: (2) f ’(x0)=tgα’ откуда следует, что производная функции в точке

равна тангенсу угла наклона касательной к графику функции в этой точке.

Понятие дифференцируемости ф-ии

Df : Ф-ия 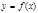дифференцируема в точке х₀ , если приращение ф-ии в точке сможет быть представлено в виде:

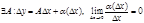, А – const.

Dh: Для дифференцирования ф-ии в т. х₀ , необходимо и достаточно, чтобы в этой точке существовала производная.

Доказательство: (необходимость)

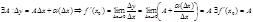
(достаточность):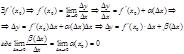

Правила диференц суммы,разн,произв,частн

1) ;

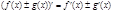2) 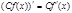, где 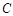- постоянная;

3) ;

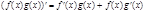4) ;

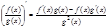5) если 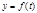, а 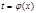, то производная сложной функции 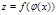находится по формуле

,

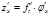где индексы указывают, по какому аргументу производится дифференцирование.