Наибольшее и наименьшее значения
Функции на отрезке

Найдите наибольшее и наименьшее значения заданной функции на заданном отрезке:
5.1) 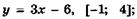
5.2) 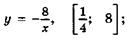
5.3) 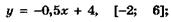
5.4) 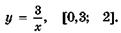
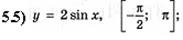
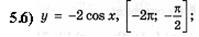
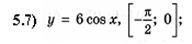
5.8) 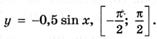
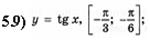
5.10) 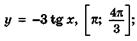
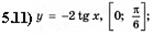
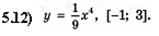
5.13) 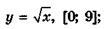
5.14) 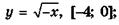
5.15) 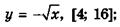
5.16) 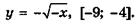
5.17) 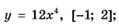
5.18) 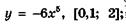
5.19) 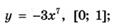
5.20) 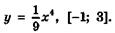
5.21) 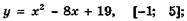
5.22) 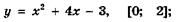
5.23) 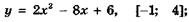
5.24) 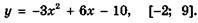
Найдите наибольшее и наименьшее значения функции 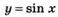 на отрезке:
на отрезке:
5.25) 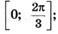
5.26) 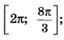
5.27) 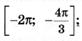
5.28) 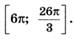
Найдите наибольшее и наименьшее значения функции
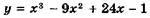 на отрезке:
на отрезке:
5.29) 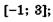
5.30) 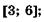
5.31) 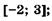
5.32) 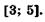
Найдите наибольшее и наименьшее значения функции
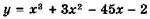 на отрезке:
на отрезке:
5.33) 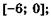
5.34) 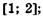
5.35) 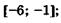
5.36) 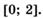
Найдите наибольшее и наименьшее значения функции
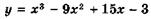 на отрезке:
на отрезке:
5.37) 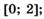
5.38) 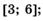
5.39) 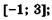
5.40) 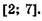
Найдите наибольшее и наименьшее значения функции
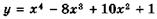 на отрезке:
на отрезке:
5.41) 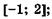
5.42) 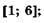
5.43) 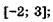
5.44) 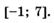
Найдите наибольшее и наименьшее значения функции
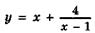 на отрезке:
на отрезке:
5.45) 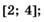
5.46) 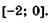
Найдите наибольшее и наименьшее значения заданной функции на заданном промежутке:
5.47) 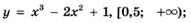
5.48) 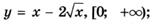
5.49) 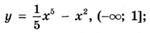
5.50) 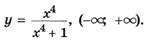
5.51) 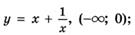
5.52) 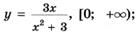
5.53) 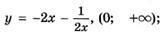
5.54) 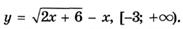
5.55) 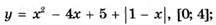
5.56) 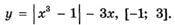
Найдите область значений функции:
5.57) 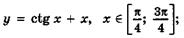
5.58) 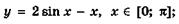
5.59) 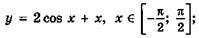
5.60) 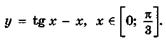
5.61) 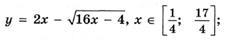
5.62) 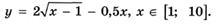 .
.
5.63) 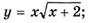
5.64) 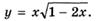
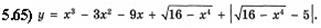
Ответы
| ymax = 6 ymin = –9 | ymax = –43 ymin = –72 | ||
| ymax = –1 ymin = –32 | ymax = 173 ymin = 45 | ||
| ymax = 5 ymin = 1 | ymax= –2 ymin= –72 | ||
| ymax = 10 ymin = 3/2 | ymax = 4 ymin = –3 | ||
| ymax = 2 ymin = –2 | ymax = –12 ymin = –28 | ||
| ymax = 2 ymin = –2 | ymax = 4 ymin = –28 | ||
| ymax = 6 ymin = 0 | ymax= 4 ymin= –28 | ||
| ymax = ½ ymin = –1/2 | ymax = 20 ymin = –7 | ||
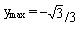 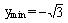 | ymax = 4 ymin = –124 | ||
ymax = 0 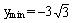 | ymax = 121 ymin = –44 | ||
ymax = 0 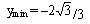 | ymax= 148 ymin= –124 | ||
| ymax = ½ ymin = 0 | ymax= 6 ymin= 5 | ||
| ymax = 3 ymin = 0 | ymax= –3 ymin= –4 | ||
| ymax = 2 ymin = 0 |  не существует, не существует,  | ||
| ymax = –2 ymin = –4 |  не существует, не существует, 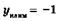 | ||
| ymax = –2 ymin = –3 | 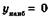 , ,  не существует не существует | ||
| ymax = 192 ymin = 0 | 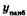 не существует не существует  | ||
| ymax = –3/50000 ymin = –192 | 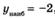 , ,  не существует не существует | ||
| ymax = 0 ymin = –3 | 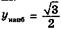 , , 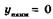 | ||
| ymax = 9 ymin = 0 | 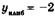 , ,  не существует не существует | ||
| ymax = 28 ymin = 3 | 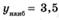 , ,  не существует не существует | ||
| ymax = 9 ymin = –3 | ymax= 8 ymin= 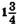 | ||
| ymax = 16 ymin = –2 | ymax= 17 ymin=–3. | ||
| ymax = –7 ymin = –199 | 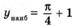 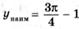 | ||
| ymax = 1 ymin = 0 | 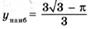 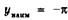 | ||
| ymax = 1 ymin = 0 | 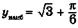 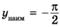 | ||
| ymax =1 ymin = 0 | 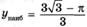 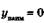 | ||
| ymax=1 ymin= –1 | 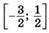 | ||
| ymax = 19 ymin = –35 | 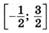 | ||
| ymax = 35 ymin = 15 | 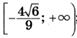 | ||
| ymax = 19ymin = –93 | 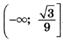 | ||
| ymax= 19ymin= 15 | 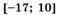 | ||
| ymax = 173 ymin = –2 |
Применение производной для исследования функций на монотонность и экстремумы

Теорема 1. Если во всех точках открытого промежутка X выполняется неравенство (причем равенство либо не выполняется, либо выполняется лишь в конечном множестве точек), то функция возрастает на промежутке X.
Теорема 2. Если во всех точках открытого промежутка X выполняется неравенство (причем равенство либо не выполняется, либо выполняется лишь в конечном множестве точек), то функция убывает на промежутке X.
Теорема 3 (достаточные условия экстремума). Пусть функция 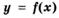 непрерывна на промежутке X и имеет внутри промежутка стационарную или критическую точку
непрерывна на промежутке X и имеет внутри промежутка стационарную или критическую точку 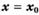 . Тогда:
. Тогда:
а) если у этой точки существует такая окрестность, в которой при 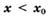 выполняется неравенство
выполняется неравенство 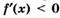 , а при
, а при 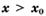 — неравенство
— неравенство 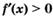 , то
, то 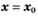 — точка минимума функции
— точка минимума функции 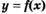 ;
;
б) если у этой точки существует такая окрестность, в которой при 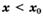 выполняется неравенство
выполняется неравенство 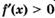 , а при
, а при 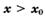 — неравенство
— неравенство 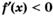 , то
, то 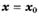 — точка максимума функции
— точка максимума функции 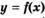 ;
;
