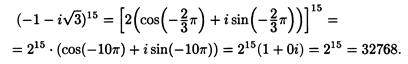Модуль и аргумент комплексного числа. Тригонометрическая форма записи

Определение 8.3 (1).

Длина |z| вектора z = (x,y) называется модулем комплексного числа z = х + yi

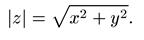
Поскольку длина каждой стороны треугольника не превосходит суммы длин двух других его сторон, а абсолютная величина разности длин двух сторон треугольника не меньше длины третьей стороны, то для любых двух комплексных чисел z₁ и z₂ имеют место неравенства

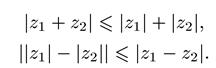
Определение 8.3 (2).

Аргумент комплексного числа. Если φ — угол, образованный ненулевым вектором z с действительной осью, то всякий угол вида (φ + 2πn, где n — целое число, и угол только такого вида, также будет углом, образованным вектором z с действительной осью.

Множество всех углов, которые образует ненулевой вектор z = = (x, у) с действительной осью, называется аргументом комплексного числа z = х + уi и обозначается arg z. Каждый элемент этого множества называется значением аргумента числа z (рис. 8.3(1)).

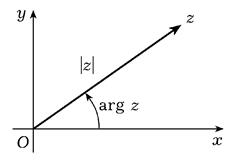
Рис. 8.3 (1).

Поскольку ненулевой вектор плоскости однозначно определяется своей длиной и углом, который он образует с осью ж, то два комплексных числа, отличные от нуля, равны тогда и только тогда, когда равны их абсолютные величины и аргументы.

Если на значения аргумента φ числа z наложить, например, условие 0≤φ<2π или условие —π<φ≤π, то значение аргумента будет определено однозначно. Такое значение называется главным значением аргумента.

Определение 8.3.(3)

Тригонометрическая форма записи комплексного числа. Действительная и мнимая части комплексного числа z = х + уi ≠ 0 выражаются через его модуль r= |z| и аргумент φ следующим образом (из определения синуса и косинуса):

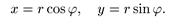
Отсюда

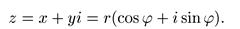
Правая часть этого равенства называется тригонометрической формой записи комплексного числа z. Мы будем ее употреблять и для z = 0; в этом случае r = 0, а φ может принимать любое значение — аргумент числа 0 не определен. Итак, всякое комплексное число можно записать в тригонометрической форме.

Ясно также, что если комплексное число z записано в виде

z =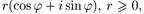

то число r является его модулем, так как

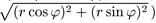, а φ одним из значений его аргумента

Тригонометрическую форму записи комплексных чисел бывает удобно использовать при перемножении комплексных чисел, в частности, она позволяет выяснить геометрический смысл произведения комплексных чисел.

Найдем формулы для умножения и деления комплексных чисел при тригонометрической форме их записи. Если

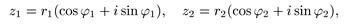
то по правилу умножения комплексных чисел (используя формулы синуса и косинуса суммы)

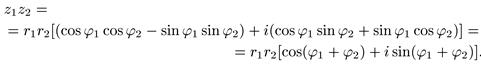
Таким образом, при умножении комплексных чисел их абсолютные величины перемножаются, а аргументы складываются:

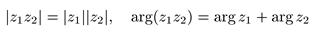
Применив эту формулу последовательно к n комплексным числам, получим

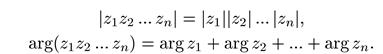
Если все n чисел равны, получим

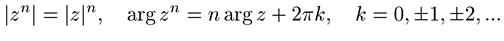
Откуда для

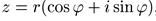
выполняется

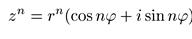
Отсюда для комплексного числа, абсолютная величина которого равна 1 (следовательно, оно имеет вид

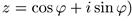
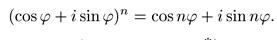
Это равенство носит название формулы Муавра

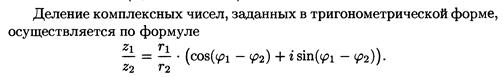
Иначе говоря, при делении комплексных чисел их модули делятся,

а аргументы вычитаются.

Примеры 8.3 (1).

Изобразить на комплексной плоскости С множества точек, удовлетворяющих следующим условиям:

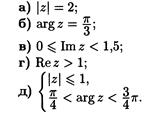
а) Поскольку 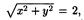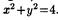, соответствующее множество точек |z|=2 – это окружность радиуса 2 (уравнение окружности с центром в начале координат x² + y² = R²

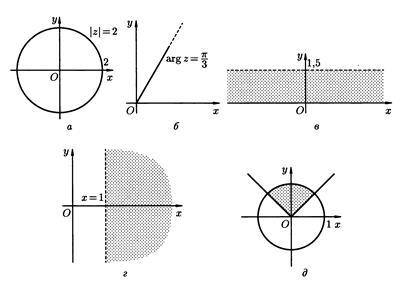
Рис. 8.3.(2)

Пример 8.3.(3)

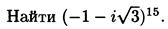
Запишем число 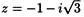в тригонометрической форме

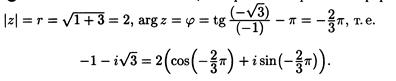
Отсюда по формуле Муавра