Тригонометрическая форма записи комплексного числа
Если точка z комплексной плоскости имеет декартовые координаты (х, у), т.е.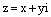 
и полярные 
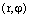, то они связаны соотношением (1):
.
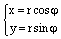По определению,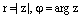 
и из (1) получаем:
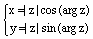. (9)
Подставляя в алгебраическую форму записи числа z получаем: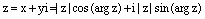 
. Или
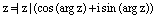(10)
Определение. Запись комплексного числа в виде (3) называется еготригонометрической формой.
Замечание. Поскольку одну букву писать экономнее нежели несколько, то чаще всего тригонометрическую форму комплексного числа пишут в виде:
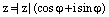, (11)
где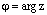 
.
Теорема. (О равенстве комплексных чисел в тригонометрической форме.)
Два комплексных числа равны тогда и только тогда, когда равны их модули и аргументы.
Доказательство. Так как между всеми комплексными числами и всемиточками комплексной плоскости существует взаимно однозначное соответствие, то равные комплексные числа отождествляются накомплексной плоскости с одной и той же точкой, следовательно, имеют одни и те же полярные координаты, т.е. полярный радиус, который по определению равен модулю комплексного числа, и полярный угол, который по определению равен аргументу комплексного числа. Обратно, если комплексные числа имеют равные модули и аргументы, то они изображаются на комплексной плоскости одной точкой и, следовательно, равны.
Теорема доказана.
Используя соотношения, которые связывают полярные и декартовыекоординаты точки плоскости, можно найти модуль и аргумент комплексного числа зная его действительную и мнимую части.
Сопряжённые числа
Геометрическое представление сопряжённых чисел
Если комплексное число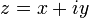 
, то число 
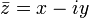называется сопряжённым (или комплексно сопряжённым) к 
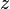(обозначается также 
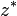). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.
Переход к сопряжённому числу можно рассматривать как одноместную операцию; перечислим её свойства.
· 
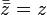(сопряжённое к сопряжённому есть исходное).
· 
· 
· 
· 
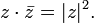
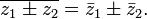
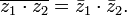
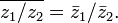
Обобщени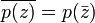е: 
, где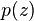 
— произвольный многочлен с вещественными коэффициентами.
· 
· 
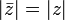
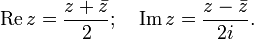
Значимость сопряжения объясняется тем, что оно является образующей группы Галуа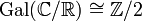 
.
1.10
Формула Муавра для комплексных чисел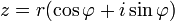 
утверждает, что
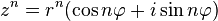
для любого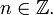 
Доказательство
Формула Муавра сразу следует из формулы Эйлера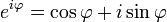 
и тождества для экспонент 
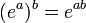, где b — целое число.[1]
Применение
Аналогичная формула применима также и при вычислении корней n-ой степени из ненулевого комплексного числа:
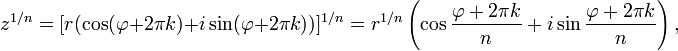
где k = 0, 1, …, n—1.
Из основной теоремы алгебры следует, что корни n-й степени из комплексного числа всегда существуют, и их количество равно n. На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного n-угольника, вписанного в окружность радиуса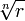 
с центром в нуле.
1.11
1.12