Тригонометрическая форма комплексного числа.
Введём величину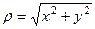 
тогда 
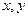можно представить в таком виде: 
, 
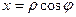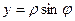для некоторого 
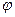, ведь геометрически в этом случае 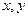- катеты прямоугольного треугольника, 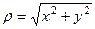- его гипотенуза.
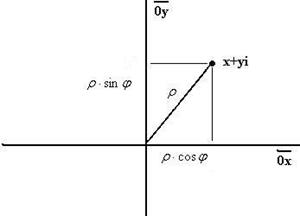
Абсцисса и ордината точки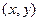 
на плоскости это проекции на оси, они равны 
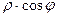и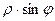 
соответственно. Кстати, эти величины 
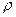и 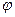называются полярными координатами точки на плоскости.
Если записать комплексное число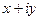 
с помощью введённых выше величин 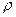и 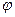, получим:
= 
= 
.
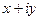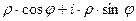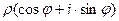Выражение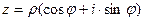 
называется тригонометрической формой комплексного числа, 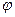- его аргументом, 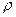- модулем.
.
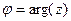
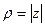Понятие модуля не противоречит известному понятию, применявшемуся раньше для отрицательных чисел: и там, и здесь модуль - есть расстояние по кратчайшей линии до начала координат.
Для любой точки 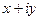модуль вычисляется как 
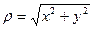. Для вычисления аргумента верна формула 
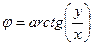если точка в 4-й и 1-й четверти, либо 
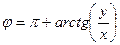, если во 2-й и 3-й четверти. Это связано с тем, что период тангенса равен 
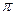, график этой функции непрерывен на интервале от 
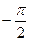до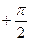 
.
Так, число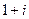 
запишется в виде 
.
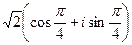Число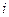 
соответствует 
.
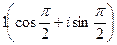Если вычислить синус и косинус, то снова перейдём к обычной, «алгебраической» форме числа:
= 
= .
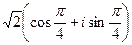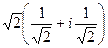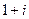Действительное число имеет аргумент 0 (если оно положительно) или 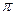(если оно отрицательно).
Угол может определяться разными способами, так, например, вместо угла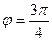 
во всех вычислениях для комплексных чисел в тригонометрической форме можно использовать 
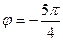, и это не будет ошибкой, так как тригонометрические функции повторяются через промежуток 
.
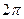Показательная форма комплексного числа.
Известна формула Эйлера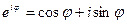 
, таким образом, выражение 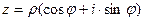может быть записано в виде 
.
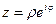Так, например, мнимой единице соответствует аргумент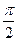 
и модуль 1, поэтому запись в тригонометрической и показательной формах такова:
.
= 
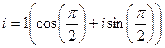
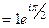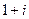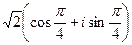
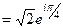
Умножение и деление в тригонометрической и показательной форме.
Умножение, и особенно деление комплексных чисел чаще всего бывает легче выполнять в тригонометрической форме, чем в алгебраической, так как для деления не нужно домножать на сопряжённое в знаменателе.
В показательной форме.
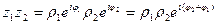
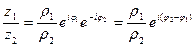
В тригонометрической форме:
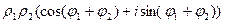
Доказательство формулы :
= 
=
=
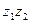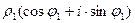
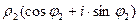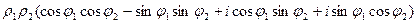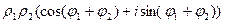
Здесь были использованы известные тригонометрические формулы косинуса суммы и синуса суммы.
Таким образом, для умножения двух комплексных чисел, представленных в тригонометрической форме, достаточно просто умножить их модули и сложить аргументы.
Формула деления двух комплексных чисел в тригонометрической форме:
= 
.
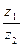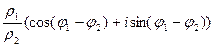Для деления двух комплексных чисел, представленных в тригонометрической форме, нужно поделить их модули и вычесть аргументы.
Заметим, что при умножении на мнимую единицу 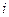, а именно при действии 
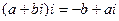, фактически вектор 
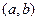на плоскости переходит в 
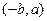, то есть как раз и прибавляется аргумент числа 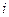, то есть 90 0.
Пример. Поделить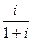 
.
= 
= 
= 
=
= 
.
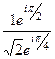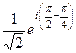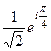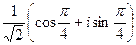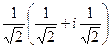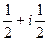Можно выполнить это деление и с помощью умножения на сопряжённое, чтобы повторить ранее изученный алгоритм:
= 
= 
= 
= .
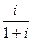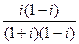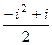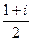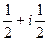