Общие понятия теории рядов. Свойства рядов. Необходимый признак сходимости числового ряда

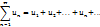
Где 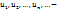действительные или комплексные числа, называемые членами ряда, 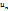- общим членом ряда.

Ряд считается заданным, если известен общий член ряда 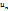, выраженный как функция его номера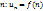

Сумма первых 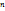членов ряда- 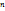-й

Если последовательность частичных сумм данного ряда имеет предел S т.е.

,

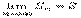то рядсходится и S – его сумма. Записывается это следующим образом:a1 + a2 + a3 + … + a_n + … = S, или 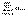= S.(a=u)

если не существует или равен бесконечности называют расходящимся.

1. Если ряд сходится и его сумма равна S то ряд 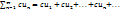где с произвольное число, также сходится и его сумма равна сS. Если же ряд расходится и с≠0 то и ряд расходится.

2. Если сходится ряд 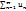и сходится ряд 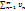а их суммы равны 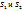соответственно то сходятся и ряды 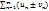, причем сумма каждого равна соответственно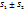

3. Если к ряду 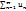прибавить( или отбросить) конечное число членов, то полученный ряд и изначальный ряд сходятся или расходятся одновременно.

Необх. Признак сходимости:Если ряд сходится то его общий член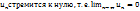

Дост. Условие расходимости если 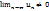или этот предел не сущ. То ряд расходится.