Необходимый признак сходимости числового ряда. Операции над числовыми рядами

Теорема 10.2.

Если ряд 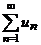сходится, то его общий член стремится к нулю, то есть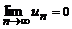

Следствие

Если, 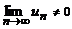то ряд 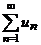расходится.

Пример 10.3.

Исследуем сходимость ряда .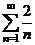

Найдем: 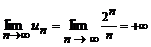(в числителе стоит показательная функция от n, которая растет быстрее, чем n), таким образом, ряд расходится.

Пример 10.4.

Исследуем сходимость гармонического ряда .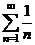

Имеем 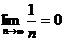, однако гармонический ряд расходится. Действительно, если предположить, что он сходится и его сумма равна S, то .

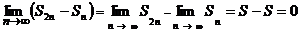С другой стороны S_2n – S_n =

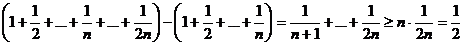, откуда .

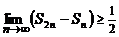Получили противоречие, следовательно, гармонический ряд 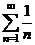расходится.

Теорема 10.3.

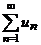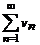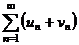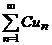Если сходятся ряды , , то сходятся ряды и (c – постоянная величина).

При этом, = + , = .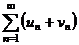

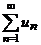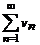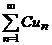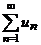Знакоположительные ряды

Определение 10.4.

Ряд 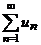называется знакоположительным, если для любого номера n u_n ≥ 0.

Ниже приведены некоторые достаточные признаки сходимости знакоположительных рядов.

Теорема 10.4. (признак сравнения).

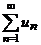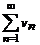Даны два ряда (а) и (б).

Если, начиная с некоторого n, выполняется условие u_n ≤ v_n и ряд (б) сходится, то сходится и ряд (а). Если же ряд (а) расходится, то ряд (б) тоже расходится.

Теорема 10.5. (признак сравнения в предельной форме).

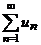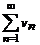Даны два ряда: (а) и (б).

Если существует конечный и не равный нулю предел 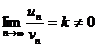, то ряды (а) и (б) сходятся или расходятся одновременно.

Замечание 10.1.

В качестве эталонных рядов для сравнения удобно выбрать:

1) гармонический ряд 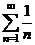, который расходится;

2) обобщенный гармонический ряд 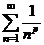(ряд Дирихле), который сходится при p > 1 и расходится при р ≤ 1;

3) геометрическую прогрессию 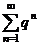, которая сходится, если 0 ≤ q < 1, и расходится, если q > 1.

Признак сравнения в предельной форме особенно эффективен для рядов, общий член которых есть алгебраическая функция аргумента n либо эквивалентная ей функция.

Пример 10.5.

Исследуем сходимость ряда .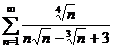

Ряд знакоположительный, применим к нему признак сравнения в предельной форме, сравнив его с рядом 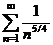, который сходится как обобщенный гармонический ряд с р = 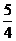> 1.

Имеем .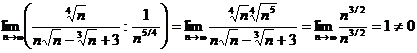

Предел отношения общих членов этих рядов при n → ∞ конечный, не равный нулю, следовательно, ряды ведут себя одинаково.

Ряд для сравнения подбираем следующим образом:

при n → ∞ ; .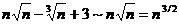

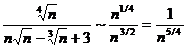Таким образом, исходный ряд сходится.

Пример 10.6.

Исследуем сходимость ряда .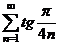

Ряд знакоположительный. Так как при n → ∞ аргумент 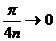, то 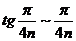, поэтому для сравнения берем ряд .

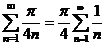Последний ряд является гармоническим, все члены которого умножены на 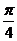, что не влияет на его расходимость.

Так как 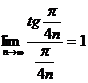и ряд 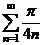расходится, то ряд 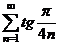также расходится.

Теорема 10.6 (признак Даламбера).

Дан ряд 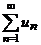, u_n > 0 для всех n /N .

Если существует 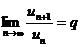, то при q < 1 ряд сходится, при q > 1 ряд расходится, при q = 1 вопрос о сходимости ряда остается открытым.

Замечание 10.2.

Признак Даламбера не дает результата для рядов с общим членом в виде дробно-рациональной функции или функции, содержащей под радикалом переменную n, так как замена n на n + 1 не меняет коэффициента при старших степенях n. Признак эффективен в случае наличия в общем члене ряда показательной функции или факториала n! = .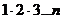

Пример 10.7.

Исследуем сходимость ряда 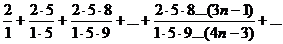с помощью признака Даламбера.

Здесь u_n= 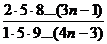, u_n+1= .

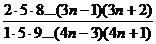Тогда q = .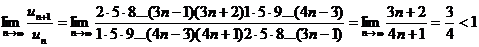

Ряд сходится, так как q < 1.

Пример 10.8.

Исследуем сходимость ряда .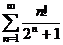

Имеем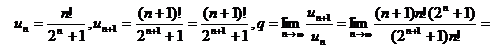

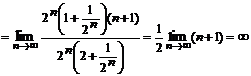
Так как q > 1, то ряд расходится.

Теорема 10.7. (радикальный признак Коши).

Дан ряд .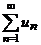

Если существует 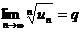, то

при q < 1 ряд сходится,

при q >1 ряд расходится,

при q = 1 вопрос о сходимости ряда остается открытым.

Замечание 10.3.

Радикальный признак Коши дает результат в случае, когда общий член ряда имеет вид степенно-показательной функции целочисленного аргумента.

Пример 10.9.

Исследуем сходимость ряда .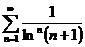

Ряд знакоположительный, применим к нему признак Коши.

Имеем q= .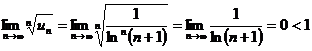

По радиальному признаку Коши ряд сходится.

Теорема 10.8. (интегральный признак Коши).

Дан ряд 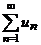. Если функция y=f(x) удовлетворяет следующим условиям:

1) f(x)=u_n; 2) непрерывна, положительна и монотонно убывает при 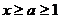, то ряд 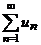и несобственный интеграл 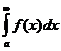сходятся или расходятся одновременно.

Замечание 10.4.

Интегральный признак Коши удобно применять в тех случаях, когда функция f(x) имеет легко находимую первообразную.

Пример 10.10.

Исследуем сходимость ряда Дирихле .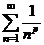

Рассмотрим функцию .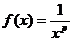

1) p > 0.

При натуральных значениях аргумента значения функции совпадают с соответствующими членами ряда 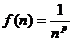. Кроме того, f(x) при x ≥ 1 будет непрерывной, положительной и монотонно убывающей.

Рассмотрим несобственный интеграл

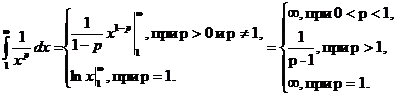
Интеграл сходится при p>1, расходится при 0<p<1, следовательно, по интегральному признаку Коши ряд 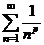сходится при >1, расходится при 0<p<1.

2) p≤0.

Проверим необходимый признак сходимости:

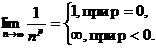, откуда 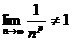, следовательно, ряд расходится при p≤0.

Пример 10.11.

Исследуем сходимость ряда .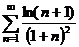

Рассмотрим функцию 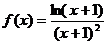. При натуральных значениях аргумента значения совпадают с соответствующими членами ряда: 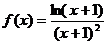. Кроме того, f(x) при x≥1 ,будет непрерывной, положительной и монотонно убывающей (функция (x+1)², стоящая в знаменателе, растет быстрее, чем функция ln(x+1), стоящая в числителе).

Рассмотрим несобственный интеграл 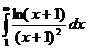, который берётся по частям. Имеем u=ln(x+1), du= 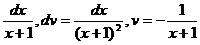, откуда

.

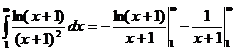Найдем .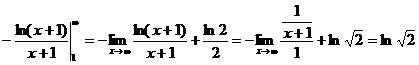

(здесь для нахождения предела, было, применено правило Лопиталя).

Далее 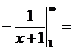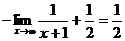, следовательно, .

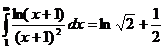Таким образом, интеграл сходится, а значит, сходится и данный ряд.

Знакочередующиеся ряды

Определение 10.5.

Ряд называется знакочередующимся, если он имеет вид

.

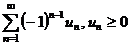Теорема 10.9. (признак Лейбница).

Если члены знакочередующегося ряда не возрастают по абсолютной

величине с ростом n, то есть, начиная с некоторого n верно неравенство u_n+1≤u_n и

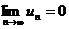, то ряд 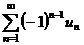сходится. Причем, если его сумма равна S, то 0≤S≤u₁.

Пример 10.12.

Исследуем сходимость ряда .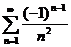

Ряд знакочередующийся. Применим признак Лейбница.

Имеем 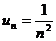, 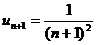. Очевидно, что 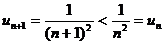. Кроме того, .

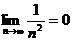Выполнены оба условия признака Лейбница, следовательно, ряд сходится.

Пример 10.13.

Исследуем сходимость ряда .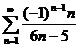

Данный ряд знакочередующийся. Члены этого ряда по абсолютной величине монотонно убывают. В самом деле,

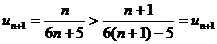, так как .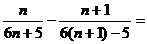

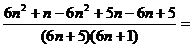
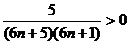Однако, .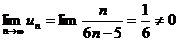

Значит, ряд расходится по необходимому признаку (следствие к теореме 10.2).

Если для знакочередующегося ряда выполнены условия теоремы 10.9, то он называется рядом лейбницева типа.

Знакопеременные ряды

Определение 10.6.

Ряд 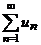называется знакопеременным, если членами его являются любые вещественные числа.

Определение 10.7.

Ряд 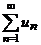называется абсолютно сходящимся, если сходится ряд .

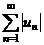Теорема 10.10.(признак абсолютной сходимости)

Дан ряд 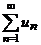, u_n 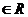. Если сходится ряд 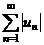, то сходится и ряд .

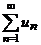Замечание 10.5.

Так как знакочередующийся ряд – частный случай знакопеременного ряда, то и к знакочередующемуся ряду можно применить признак абсолютной сходимости.

Пример 10.14.

Исследуем сходимость ряда .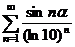

Данный ряд знакопеременный. Применим к нему признак абсолютной сходимости.

Составим ряд из абсолютных величин членов исходного ряда: 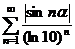. Этот знакоположительный ряд сравним в непредельной форме с рядом 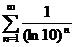, который представляет собой геометрическую прогрессию с 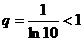, следовательно, 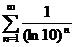сходится.

Имеем очевидное неравенство 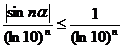, откуда ряд 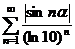также сходится, а значит, по признаку абсолютной сходимости исходный ряд сходится абсолютно.

Определение 10.8.

Если ряд 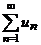сходится, а ряд 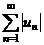расходится, то ряд 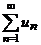называется условно сходящимся.

Пример 10.15.

Исследуем на абсолютную или условную сходимость так называемый ряд

Лейбница .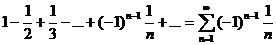

По признаку Лейбница этот ряд сходится, так как для него выполняются оба условия этого признака:

а) 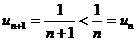и б) .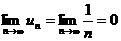

Но ряд, составленный из абсолютных величин данного ряда 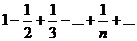является гармоническим, а значит, расходится.

Следовательно, ряд Лейбница сходится условно.

Теорема 10.11.

В сходящемся (абсолютно или условно) ряде можно группировать члены, не меняя их порядка. Иными словами, если сходится ряд u₁+u₂+…+u_n+…, то сходится и ряд (u₁+u₂+…+u_n)+ (u_n+1+u_n+2+…+u_l)+ (u_l+1+u_l+2+…+u_m)+…, причем оба ряда имеют одну и ту же сумму.

Теорема 10.12.

Абсолютно сходящийся ряд остаётся сходящимся и сохраняет сумму при любой перестановке его членов.

Теорема 10.13.

В условно сходящемся ряде при соответствующей перестановке его членов можно сделать его сумму равной любому наперед заданному числу или сделать ряд расходящимся.

Определение 10.9.

Произведением рядов 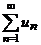и 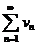называется ряд 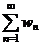, где w_n=u₁v_n+u₂v_n-1+…+u_nv₁.

Теорема 10.14.

Если перемножаемые ряды сходятся абсолютно, то ряд-произведение сходится также абсолютно и имеет сумму, равную произведению сумм рядов-сомножителей.