Інтегральні показники якості
Кожний з розглянутих вище прямих показників якості характеризує лише одну яку-небудь властивість САУ, лише одну ознаку перехідного процесу. Причому, всі показники пов'язані з настроюваними параметрами регулятора складними залежностями, що мають, як правило, суперечливий характер: зміна параметра приводить до поліпшення одних показників якості й погіршенню інших. Ця обставина істотно утрудняє вибір параметрів регулятора. Тому в інженерній практиці широко використовуються інтегральні показники або оцінки якості.
Інтегральна оцінка якості – певний інтеграл за часом (у межах від 0 до ¥) від деякої функції керованої величини y(t), або сигналу помилки e(t):
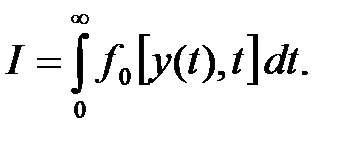 (1)
(1)
Підінтегральна функція f0 вибирається таким чином, щоб інтеграл (1) краще характеризував якість системи й простіше виражався через коефіцієнти передатної функції замкнутої системи. Щоб інтеграл був збіжним, у функцію f0 уводять не абсолютні значення y(t) або e(t), а їхнього відхилення від кінцевих, сталих значень.
Найпростішою інтегральною оцінкою є лінійна інтегральна оцінка
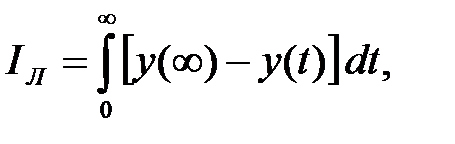 (2)
(2)
| Інтегральна оцінка (2) враховує як величину динамічних відхилень, так і тривалість іх існування. Тому чим менше оцінка, тем краще якість процесу управління. |
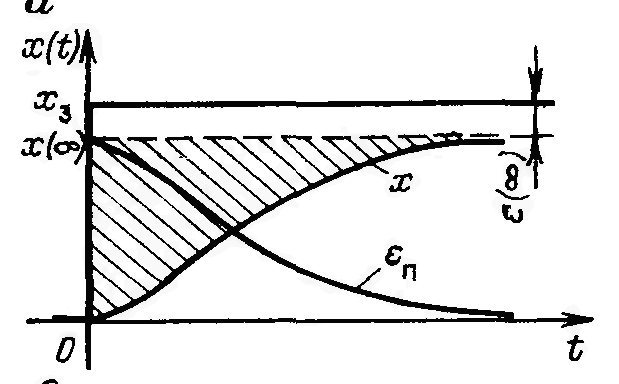
Різниця під знаком інтеграла yуст – y(t) дорівнює динамічній або перехідній складовій сигналу помилки: yуст – y(t) = x - e(¥) – y(t) = e(t) - e(¥) = eп(t).
Тому лінійна інтегральна оцінка може бути визначена:
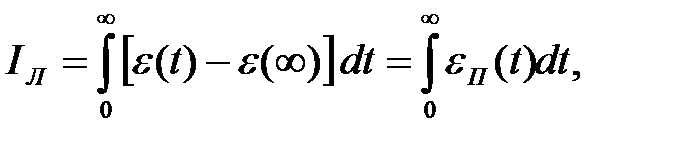
Цей інтеграл відповідає площі під кривою перехідної складової сигналу помилки eп(t), викликаної зміною впливу, що задає, або впливу, що обурює.
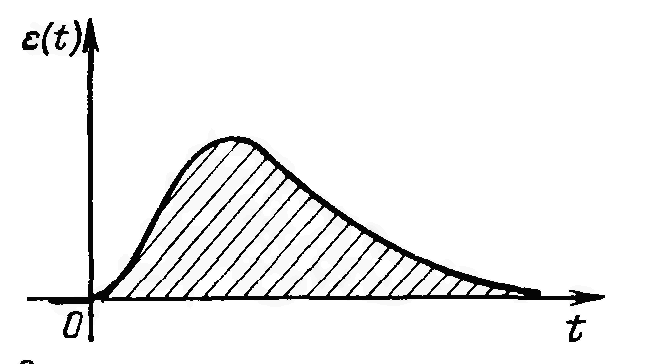
Площа під кривою eп(t) буде тим менше, ніж швидше закінчується перехідний процес і чим менше відхилення сигналу y(t) від x(t). Тому настроєчні параметри регулятора необхідно вибирати таким чином, щоб оцінка Iл була мінімальною.

Недоліком лінійної інтегральної оцінки QЛ є те, що її можна застосовувати лише для свідомо неколивальних, аперіодичних перехідних процесів. Інтеграл (2), обчислений для знакозмінній кривій 1, (мал. б) буде істотно менше інтеграла, обчисленого для аперіодичній кривій 2 (хоча якість перехідного процесу 2 явно краще).
У зв'язку із цим для коливальних перехідних процесів застосовують такі інтегральні оцінки, знакозмінність підінтегральної функції яких тим або іншим способом усунута. Такою оцінкою є, наприклад, модульна інтегральна оцінка
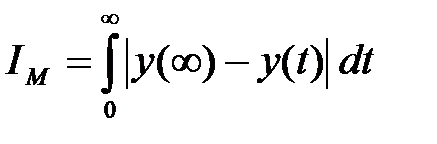 або
або 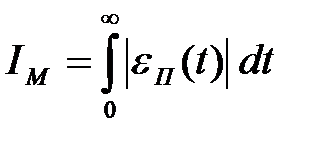 (3)
(3)
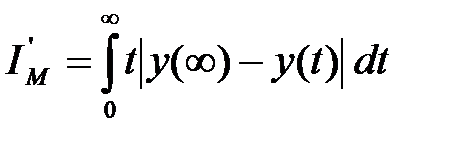 або
або 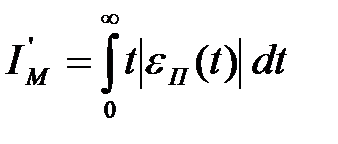 (4)
(4)
Оцінка (4) надає більшу вагу тим значенням сигналу помилки, які мають місце наприкінці перехідного процесу.
Оцінки Iм і I’м можна використовувати тільки при дослідженні систем на моделях, тому що їхнє обчислення через коефіцієнти передатної функції (без знаходження eп(t)) неможливо.
При аналізі й синтезі систем регулювання з коливальними властивостями найбільше широко використовується квадратична інтегральна оцінка
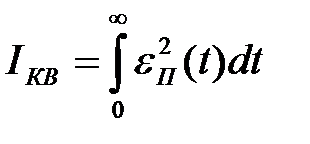 ,
,
яка дорівнює площі під кривою 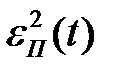 .
.
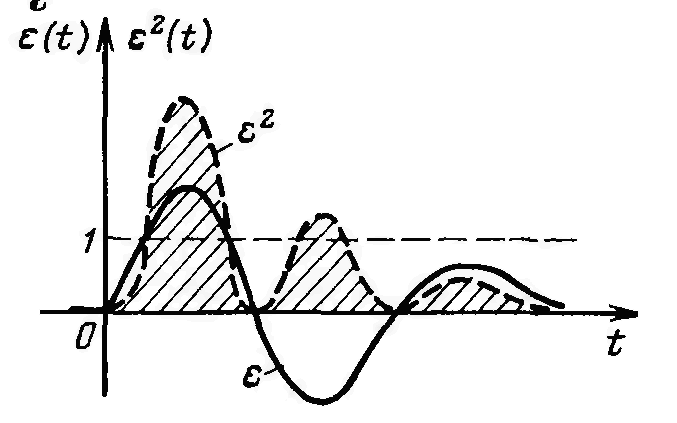
Дана квадратична оцінка, як і лінійна враховує величину й тривалість відхилень. Однак через зведення сигналу eп(t) у квадрат перші (більші) відхилення здобувають у кінцевому значенні інтеграла істотно більшу вагу, ніж наступні (малі) відхилення. Тому мінімальні значення оцінки Iкв завжди відповідають коливальним процесам з малим загасанням. Для усунення цього недоліку застосовують поліпшену квадратичну оцінку:
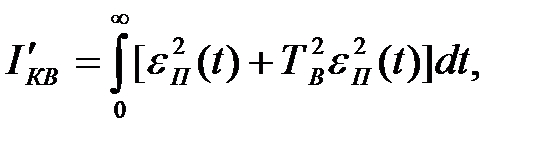
яка, крім самих відхилень, ураховує з ваговим коефіцієнтом 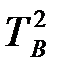 похідну відхилень. Як правило,
похідну відхилень. Як правило, 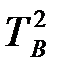 вибирають рівним бажаного часу наростання tн або в межах
вибирають рівним бажаного часу наростання tн або в межах 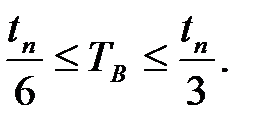
де tп – бажаний час перехідного процесу.
Слід зазначити, що абсолютне значення будь-якої інтегральної оцінки саме по собі не представляє інтересу. Воно служить лише для зіставлення різних варіантів настроювання однієї й тієї ж системи.
Всі розглянуті інтегральні показники використовують для визначення оптимальних значень настроєчних параметрів системи упраління. Оптимальним уважають такі значення, які відповідають мінімуму інтегрального показника I ® min.
11. СИНТЕЗ ЛІНІЙНИХ СИСТЕМ УПРАВЛІННЯ
