Дифференцируемость функции
Определение. Говорят, что функция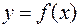 
дифференцируема в точке x0, если ее приращение 
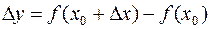можно представить в виде
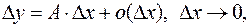(1)
где A – некоторое число, не зависящее от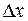 
.
Теорема 1. Для того, чтобы функция 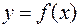, была дифференцируемой в точке x0, необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Доказательство. Необходимость. Пусть 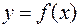дифференцируема. Разделим обе части равенства (1) на :
.
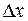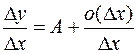Переходя к пределу при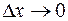 
, получим
,
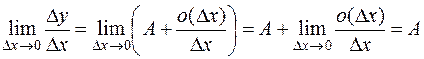т.е. в точке x0 существует производная и она равна A: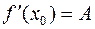 
.
Достаточность. Пусть существует конечная производная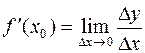 
.
Тогда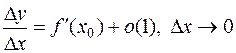 
и, следовательно,
.
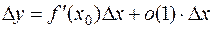В этом соотношении нетрудно увидеть равенство (1). Теорема доказана.
Таким образом, для функции одной переменной дифференцируемость и существование конечной производной – понятия равносильные.
Формулу
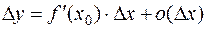
называют формулой бесконечно малых приращений.
Между понятиями дифференцируемости и непрерывности существует связь, устанавливаемая следующей теоремой.
Теорема 2. Если функция 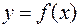дифференцируема в точке x0, то она и непрерывна в этой точке.
Действительно из формулы (1) следует, что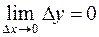 
, а это и есть одно из определений непрерывности.
Естественно возникает вопрос о том, справедливо ли утверждение, обратное теореме 2, т.е. “непрерывная функция дифференцируема”. На этот вопрос следует дать отрицательный ответ: существуют функции, непрерывные в некоторой точке, но не дифференцируемые в данной точке. Примером может служить функция из примера 2 §3: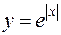 
. Она непрерывна в нуле, но 
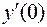не существует.
Приведем еще один пример такой функции.
Пример 1.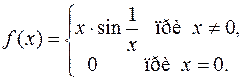 
Данная функция – неэлементарная, возможная точка разрыва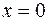 
(в этой точке одно элементарное выражение меняется на другое). Но
,
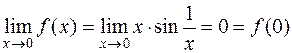следовательно,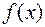 
непрерывна в точке 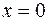. Найдем производную функции в нуле (по определению!):
.
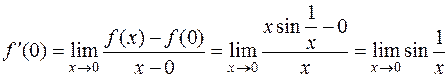Но нам уже известно, что, когда аргумент синуса стремится в ¥, синус предела не имеет. Итак,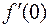 
не существует, т.е. 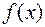недифференцируема в нуле.
Отметим, что математиками построены примеры функций, непрерывных на некотором промежутке, но не имеющих производной ни в одной точке этого промежутка.
Лекция 9