Дифференцируемость и дифференциал функции
Дифференциальное исчисление
Функций одной переменной
Производная
Пусть функция f определена в V(x0). Придадим точке х0 произвольное приращение 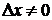 так, чтобы x0+
так, чтобы x0+ 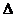 x
x 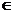 V(x0). Тогда функция f(x) получит приращение
V(x0). Тогда функция f(x) получит приращение
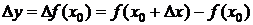 .
.
Рассмотрим 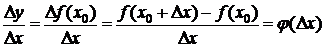 - функцию, определённую в
- функцию, определённую в 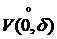 .
.
Определение 1.Производной функции f в точке х0 называется предел при 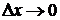 отношения приращения функции к вызвавшему его приращению аргумента, если этот предел существует.
отношения приращения функции к вызвавшему его приращению аргумента, если этот предел существует.
Обозначается 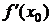 ,
, 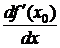 ,
, 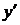 ,
, 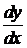 ,
, 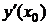 .
.
Таким образом, по определению 1 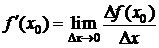 . (1)
. (1)
Обозначения 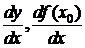 ввёл Лейбниц (1646-1716), а
ввёл Лейбниц (1646-1716), а 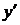 ,
, 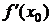 -Лагранж (1736-1813).
-Лагранж (1736-1813).
Производная функции в точке – число.
Пусть 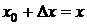 ,
, 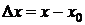 , х
, х 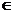 V(x0). Тогда (1) равносильно
V(x0). Тогда (1) равносильно
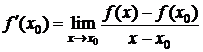 . (2)
. (2)
Если 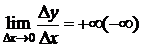 , то говорят, что в точке х0 существует бесконечная производная, равная
, то говорят, что в точке х0 существует бесконечная производная, равная 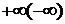 . Обозначается
. Обозначается 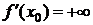 (
( 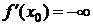 ).
).
Определение 2. Правой (левой) производной функции в точке х0 называют правый (левый) предел отношения 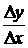 при
при 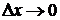 , если этот предел существует.
, если этот предел существует.
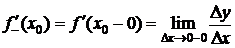 ,
, 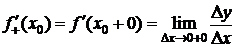 .
.
Правая и левая производные называются односторонними производными в точке х0.
Справедливо следующее утверждение: функция f имеет в точке х0 производную тогда и только тогда, когда 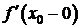 и
и 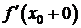 существуют и равны. Тогда
существуют и равны. Тогда 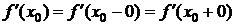 .
.
Пусть f имеет производную 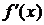 в каждой точке
в каждой точке 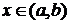 . Поставим в соответствие точке х производную функции в этой точке:
. Поставим в соответствие точке х производную функции в этой точке: 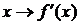 ,
, 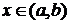 . Это соответствие определяет функцию
. Это соответствие определяет функцию 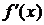 аргумента х, определённую на
аргумента х, определённую на 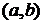 . Она называется производной функцией от функции f.
. Она называется производной функцией от функции f.
Значение 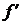 в точке х является производной функции в точке х (может быть числом,
в точке х является производной функции в точке х (может быть числом, 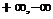 ).
).
Примеры.
1) y=f(x)=c 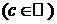 .
. 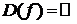 .
.
D Выберем 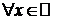 , придадим значению х приращение
, придадим значению х приращение 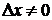 . Тогда
. Тогда
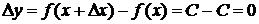 .
.
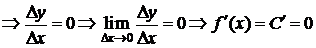
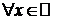 .D
.D
Производная постоянной функции тождественно равна нулю: 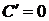 .
.
2) y=f(x)=x, 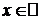 .
.
D Выберем 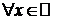 , придадим значению х приращение
, придадим значению х приращение 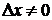 . Тогда
. Тогда
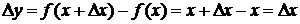
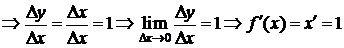
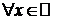 . D
. D
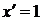 .
.
3) y=f(x)=|x| 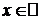 .
.
D Пусть х<0, 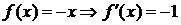 .
.
Пусть х>0, 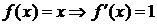 .
.
Пусть х=0, 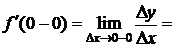
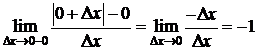 ,
,
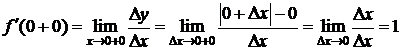 .
.
Т.к. 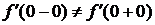 ,то
,то 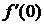 не существует. D
не существует. D
Физический смысл производной и дифференциала
Пусть f(x) определена в 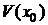 . Придадим точке x0 приращение
. Придадим точке x0 приращение 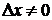 , тогда приращение функции
, тогда приращение функции 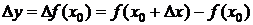 . Пусть
. Пусть 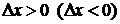 . Отношение
. Отношение 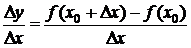 -это средняя скорость изменения переменной y на отрезке
-это средняя скорость изменения переменной y на отрезке 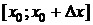
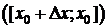 относительно х.
относительно х.
 - мгновенная скорость изменения переменной у в точке x0 относительно х.
- мгновенная скорость изменения переменной у в точке x0 относительно х.
Таким образом 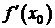 - скорость функции
- скорость функции 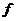 в точке х0. Тогда если f описывает некоторый процесс любого характера (механического, биологического, химического и т.д.), то f ¢ - скорость изменения этого процесса в точке х0.
в точке х0. Тогда если f описывает некоторый процесс любого характера (механического, биологического, химического и т.д.), то f ¢ - скорость изменения этого процесса в точке х0.
Примеры.
1) Пусть 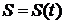 - закон движения материальной точки. В момент времени t0 точка прошла путь S0. В момент времени
- закон движения материальной точки. В момент времени t0 точка прошла путь S0. В момент времени 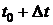 точка прошла путь S. За время Dt точка прошла путь
точка прошла путь S. За время Dt точка прошла путь 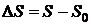 .
.
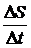 - средняя скорость движения точки между моментами времени t0 и
- средняя скорость движения точки между моментами времени t0 и 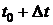 ,
,
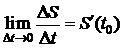 - называется скоростью движения материальной точки в момент времени t0.
- называется скоростью движения материальной точки в момент времени t0.
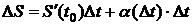 ,
, 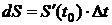 .
.
DS - путь, фактически пройденный материальной точкой за промежуток времени Dt (между t0 и  ) с переменной скоростью.
) с переменной скоростью.
dS - путь, который прошла бы точка за момент времени Dt, если бы она двигалась с постоянной скоростью ( скоростью в момент времени t0).
Если 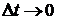 , то
, то 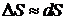 .
.
2) 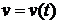 - закон изменения скорости. Рассуждаем аналогично примеру 1:
- закон изменения скорости. Рассуждаем аналогично примеру 1: 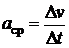 - среднее ускорение за время между t0 и
- среднее ускорение за время между t0 и 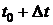 ,
, 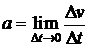 - ускорение в момент времени t0.
- ускорение в момент времени t0.
Производная показательно – степенной функции.
Примеры.
1) x=acost,
 y=asint,
y=asint, 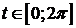 ,
,
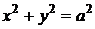 - окружность с центром в точке (0;0) радиуса а.
- окружность с центром в точке (0;0) радиуса а.
2) x=acost,
y=bsint, 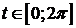 ,
,

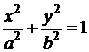 - эллипс.
- эллипс.
3) x=acost+x0,
y=asint+y0, 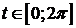 ,
,
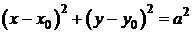 - окружность с центром в точке
- окружность с центром в точке 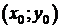 , радиуса а.
, радиуса а.
4) x=a(t-sint),
 y=a(1-cost).
y=a(1-cost).
Пусть по прямой Ох катится окружность радиуса а.
Циклоида - линия, которую при этом описывает каждая точка окружности.
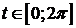 - первая арка циклоиды
- первая арка циклоиды
 При
При 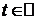 получим всю циклоиду.
получим всю циклоиду.
 5)
5) 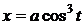 ,
,
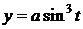 ,
, 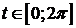 - астроида (гипоциклоида)
- астроида (гипоциклоида)
| t | 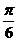 | 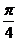 | 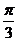 | 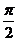 | 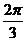 | 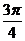 | 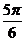 | |
| х | 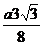 | 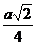 | 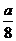 | 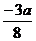 | 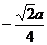 | 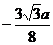 | ||
| y | 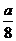 | 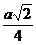 | 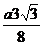 | 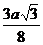 | 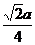 | 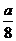 |
Построим по точкам.
| t | 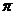 | 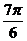 | 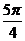 | 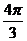 | 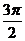 | 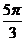 | 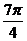 | 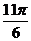 | 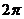 |
| х | -1 | 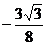 | 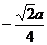 | 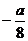 | 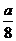 | 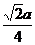 | 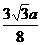 | ||
| y | 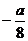 | 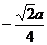 | 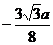 | -1 | 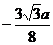 | 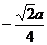 | 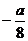 |
Из примеров видно, что кривая (1) не всегда является графиком некоторой функции, то есть уравнения (1) не всегда определяют функцию y=f(x) (хотя связывают х и у).
Пусть функция x=j(t) имеет обратную 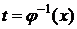 , xÎX. Подставляя
, xÎX. Подставляя 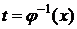 в функцию y=y(t), получим
в функцию y=y(t), получим 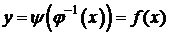 , xÎX. Таким образом, если для функции x=j(t)существует обратная функция, то система (1) определяет функцию y=f(x).
, xÎX. Таким образом, если для функции x=j(t)существует обратная функция, то система (1) определяет функцию y=f(x).
Определение.Задание функции y=f(x) с помощью системы (1) называется параметрическим заданием функции.
Если в параметрически заданной функции уравнение x=j(t) разрешимо относительно t (t=t(x)), то параметрическое задание функции можно свести к явному: 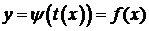 (но это не всегда можно сделать).
(но это не всегда можно сделать).
Пример.x=acost,
y=asint, 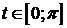 ,
,
x=j(t) монотонно убывает и непрерывна на 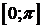 ,
, 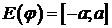 . Следовательно, существует обратная функция
. Следовательно, существует обратная функция 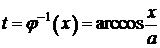 , определённая на
, определённая на 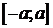 . Значит,
. Значит, 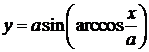 - функция от х, определённая на
- функция от х, определённая на 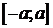 .Так как
.Так как 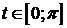 , то y>0. Значит,
, то y>0. Значит,
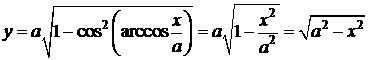 .
.
Наоборот, всякую функцию y=f(x) можно многими способами представить параметрически в виде (1). Для этого достаточно задать совершенно произвольно функцию x=j(t) параметра t. Тогда для y=f(x) становится функцией того же параметра: 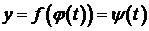 .
.
Примеры.
1) 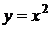 ,
, 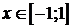 .
.
Положим 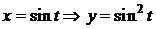 . Получаем
. Получаем
x=sint,
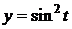 ,
, 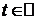 .
.
2) y=f(x), 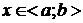 .
.
x=t,
y=f(t), 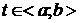 .
.
Таким образом параметрический способ задания функции является более общим.
Теорема 1. Если в системе (1) функции j(t) и y(t) непрерывны на 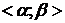 и j(t) на этом промежутке строго монотонна, то система (1) определяет непрерывную функцию y=f(x), определённую на
и j(t) на этом промежутке строго монотонна, то система (1) определяет непрерывную функцию y=f(x), определённую на 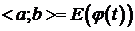 .
.
Доказательство.
 Так как j(t) непрерывна на
Так как j(t) непрерывна на 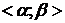 , то по следствию из II теоремы Больцано-Коши.
, то по следствию из II теоремы Больцано-Коши. 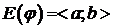 . Так как x=j(t) непрерывна и строго монотонна на
. Так как x=j(t) непрерывна и строго монотонна на 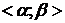 , то она имеет обратную функцию
, то она имеет обратную функцию 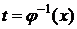 , непрерывную и строго монотонную на
, непрерывную и строго монотонную на 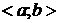 . Тогда
. Тогда 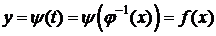 - композиция двух непрерывных функций на
- композиция двух непрерывных функций на 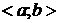 , следовательно, она является непрерывной на
, следовательно, она является непрерывной на 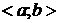 функцией.
функцией. 
Теорема 2. Пусть функция y=f(x) задана системой (1). Если функции j и y непрерывно дифференцируемы на 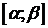 , и на этом отрезке
, и на этом отрезке 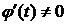 , то функция f дифференцируема на некотором промежутке D и справедлива формула
, то функция f дифференцируема на некотором промежутке D и справедлива формула
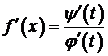
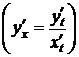 . (2)
. (2)
Доказательство.
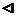 Так как
Так как 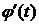 непрерывна и
непрерывна и 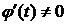 на
на 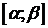 , то
, то 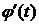 одного знака на
одного знака на 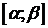 (I теорема Больцано–Коши). Следовательно (это будет доказано позже), j(t) строго монотонна на
(I теорема Больцано–Коши). Следовательно (это будет доказано позже), j(t) строго монотонна на 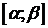 . Значит, существует обратная функция
. Значит, существует обратная функция 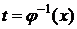 , xÎD. Так как
, xÎD. Так как 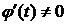 , то обратная функция дифференцируема
, то обратная функция дифференцируема 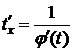 .
.
Так как y=y(t), а 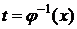 , то
, то 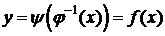 - сложная функция. Она дифференцируема на D, так как j и y дифференцируемые функции, и её производная:
- сложная функция. Она дифференцируема на D, так как j и y дифференцируемые функции, и её производная: 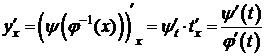 .
. 
Пример. x=acost
y=asint, 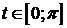 ,
, 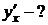
D j(t)=acost, 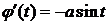 непрерывна на
непрерывна на 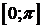 ,
, 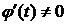 на
на 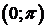 ,
,
y(t)=asint, 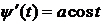
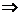
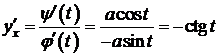 ,
, 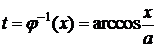 ,
, 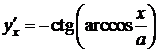 ,
, 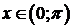 . D
. D
Замечание 1. Если 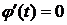 ,
, 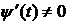 , то
, то 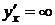 .
.
Если 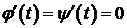 , то в этой точке
, то в этой точке 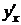 не определена (хотя это не значит, что
не определена (хотя это не значит, что 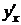 не существует).
не существует).
Например,рассмотрим функцию 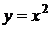 ,
, 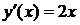 ,
, 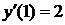 .
.
Пусть 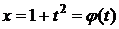 ,
, 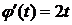 .
.
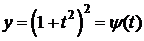 ,
, 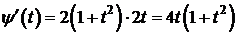 .
.
Точке t=0 соответствует точка х=1.
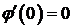 ,
, 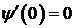 ,
, 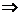
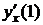 не определена.
не определена.
Если функции j(t), 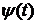 дважды дифференцируемы и
дважды дифференцируемы и 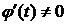 , то существует
, то существует 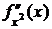 :
:
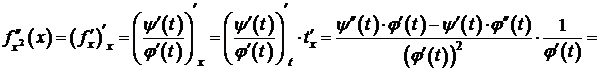
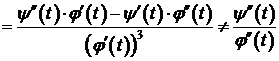 .
.
Пример 1.
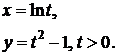 (*)
(*)
x=j(t)=lnt - непрерывная, строго монотонная при t>0 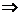 существует обратная функция
существует обратная функция 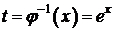 ,
, 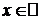 . Тогда уравнения (*) задают на
. Тогда уравнения (*) задают на 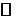 функцию y=f(x). Найдём
функцию y=f(x). Найдём 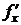 .
.
I способ: 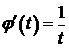 ,
, 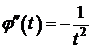 ,
, 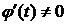 ,
,
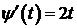 ,
, 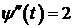 ,
,
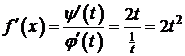 ,
, 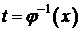 ,
,
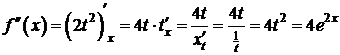 .
.
II способ: 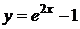
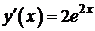 ,
, 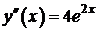 (но не всегда
(но не всегда 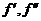 выражаются через х).
выражаются через х).
Пример 2. 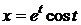
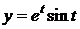 ,
, 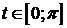 .
.
На некотором промежутке эти формулы задают функцию y=f(x).
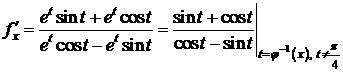
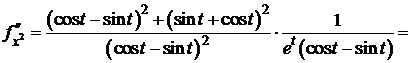
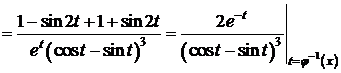
Пример 3.
D 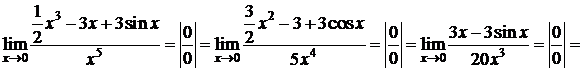
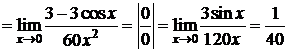 . D
. D
II. Неопределенность 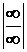 .
.
Теорема 3. Пусть
1) f и g определены и дифференцируемы в 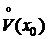 ,
, 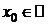 ;
;
2) g¢ (x)¹0 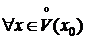 ;
;
3) 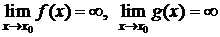 ;
;
4) существует конечный или бесконечный 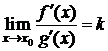 .
.
Тогда существует 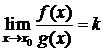 , т. е.
, т. е. 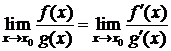 .
.
Из теоремы 3 следует правило Лопиталя раскрытия неопределенностей 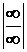 : предел отношения двух бесконечно больших функций при х®х0
: предел отношения двух бесконечно больших функций при х®х0 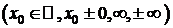 при выполнении условий 1)-4) теоремы 3 равен пределу при х®х0 отношения производных этих функций.
при выполнении условий 1)-4) теоремы 3 равен пределу при х®х0 отношения производных этих функций.
Остаются в силе замечания 1, 2.
Пример 4. D Пусть a>1.
а) 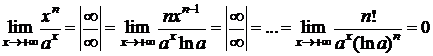 ;
;
б) 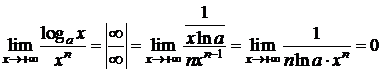 . D
. D
Вывод. Показательная функция ax (a>1) при 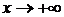 растет быстрее, чем степенная xn. Степенная функция xn при
растет быстрее, чем степенная xn. Степенная функция xn при 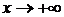 растет быстрее, чем логарифмическая logax (a>1).
растет быстрее, чем логарифмическая logax (a>1).
III. Неопределенности вида |0×¥|, |¥-¥|сводятся к неопределенностям вида 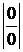 или
или 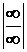 :
: 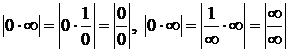 , |¥-¥| - привести к общему знаменателю.
, |¥-¥| - привести к общему знаменателю.
Пример 5. D 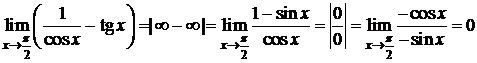 . D
. D
Пример 6.D 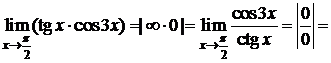
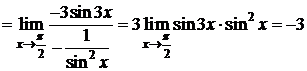 . D
. D
IV. Неопределенности 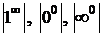 сводятся к |0×¥|, а она к
сводятся к |0×¥|, а она к 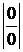 или
или 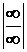 .
.
Пример 7.D  ;
;
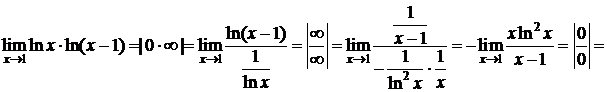
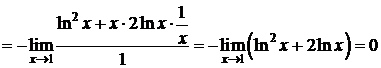 .
.
Следовательно, 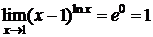 . D
. D
Пример 8. D 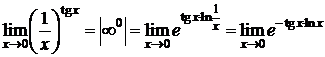 ;
;
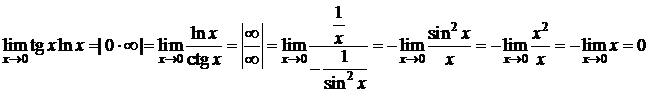 Значит,
Значит, 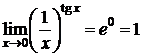 . D
. D
Замечание. Важно в случае многократного применения правила Лопиталя не забывать каждый раз проверять, раскрыта ли неопределенность, иначе можно допустить ошибку.
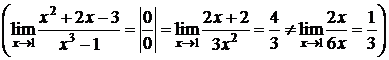
Формула Тейлора
Теорема. Пусть функция f(x) имеет в некоторой окрестности V(a) точки a производные до (n+1)-го порядка включительно. Пусть х – любая точка из V(a), p - произвольное положительное число. Тогда между точками а и х найдется такая точка с, что справедлива формула
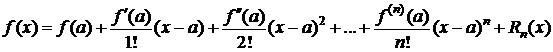 , (1)
, (1)
где 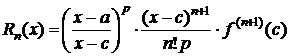 , cÎ(a;x) (или cÎ(x;a)). (2)
, cÎ(a;x) (или cÎ(x;a)). (2)
Формула (1) называется формулой Тейлора с центром в точке а, Rn(x) - остаточный член формулы Тейлора в общей форме.
Доказательство.
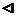 Пусть j(x;a) - многочлен n - порядка относительно х правой части формулы (1), т. е.
Пусть j(x;a) - многочлен n - порядка относительно х правой части формулы (1), т. е.
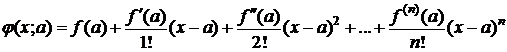 .
.
В силу условия j(x;a) существует. Обозначим через Rn(x)=f(x)-j(x;a). Тогда формула (1) будет доказана, если будет установлено, что Rn(x) имеет вид (2). Зафиксируем  . Пусть x>a (для x<a доказательство аналогично). На отрезке [a;x] рассмотрим вспомогательную функцию y(t):
. Пусть x>a (для x<a доказательство аналогично). На отрезке [a;x] рассмотрим вспомогательную функцию y(t):
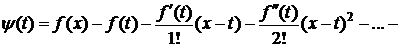
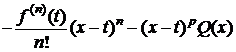 , (3)
, (3)
где 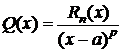 , т. е.
, т. е. 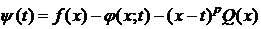 .
.
Покажем, что y(t) удовлетворяет условиям теоремы Ролля:
1) y(t) непрерывна на [a;x],
2) y(t) дифференцируема на (a;x),
3) 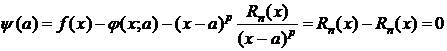 ,
,
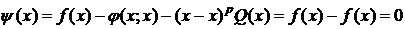 .
.
Значит, y(a)=y(x). Тогда на основании теоремы Ролля $ cÎ(a;x): y ¢(с)=0. Дифференцируя (3), получим
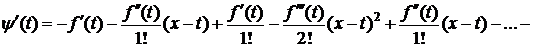
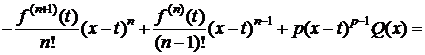
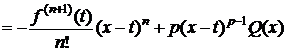 .
.
Тогда $ cÎ(a;x): 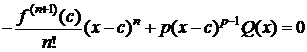 . Следовательно,
. Следовательно,
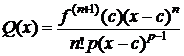 . (4)
. (4)
Тогда из (3), (4) следует
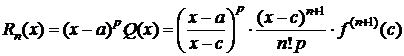 , cÎ(a;x).
, cÎ(a;x). 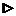
Пример.1. Найти разложение по формуле Тейлора многочлена n-й степени
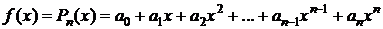 ,
, 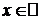 ,
, 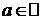 .
.
D fn+1(x)=Pn+1(x)=0 " 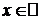 . Тогда Rn(x)=0 "
. Тогда Rn(x)=0 " 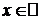 . Следовательно,
. Следовательно,
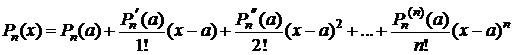 . D
. D
Остаточный член формулы Тейлора в различных формах
Преобразуем формулу (2). Т. к. cÎ(a;x), то существует такое число q, 0<q<1, что c=a+q(x-a) Þ x-c=x-a-q(x-a)=(x-a)(1-q). Тогда
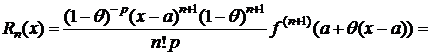
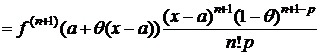 . (5)
. (5)
Частные случаи.
1) p=n+1 Þ 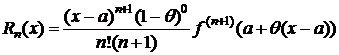 или
или
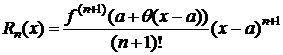 , 0<q<1. (6)
, 0<q<1. (6)
(6)– остаточный член в форме Лагранжа (наиболее употребительная форма).
2) p=1 Þ 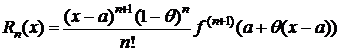 . (7)
. (7)
(7) – остаточный член в форме Коши.
Замечание 1. В формулах (6) и (7) q, вообще говоря, различны, т. к. эти формулы получены из (2) при различных значениях р, а q зависит от р.
Замечание 2. В некоторых задачах важен лишь порядок Rn(x) относительно (x-a).
Из (6) Þ 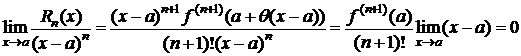
Þ 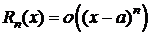 (8)
(8)
(8) - остаточный член в форме Пеано.
Замечание 3. С помощью формулы Тейлора можно производить приближенные вычисления f(x) с любой степенью точности: f(x)»j(x;a), погрешность равна Rn(x).
Замечание 4. Положим в (1) а=х0, х-х0=Dх, х=х0+Dх, f(x0+Dx)-f(x0)=Df(x0)=Dy.
Тогда 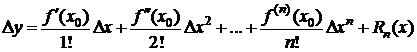 . Формула Лагранжа Dy=f(x)-f(x0)=f¢ (c)Dx является частным случаем формулы Тейлора и получается из нее при n=0. Действительно, при n=0
. Формула Лагранжа Dy=f(x)-f(x0)=f¢ (c)Dx является частным случаем формулы Тейлора и получается из нее при n=0. Действительно, при n=0
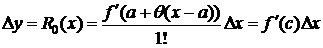 , 0<q<1.
, 0<q<1.
Формула Маклорена
Полагая в формулах (1), (6)-(8) а=0, получим
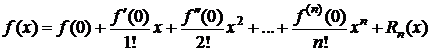 -
-
формула Маклорена;
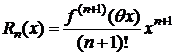 - форма Лагранжа;
- форма Лагранжа;
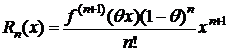 - форма Коши;
- форма Коши;
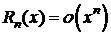 - форма Пеано.
- форма Пеано.
Разложение некоторых элементарных функций по формуле Маклорена
1. y=f(x)=ex, 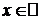 .
.
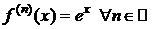 ,
, 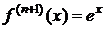 . При x=0 f(0)=f(n)(0)=1 Þ
. При x=0 f(0)=f(n)(0)=1 Þ
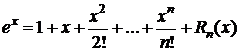 ,
,
где 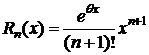 - форма Лагранжа;
- форма Лагранжа;
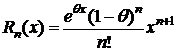 - форма Коши;
- форма Коши;
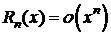 - форма Пеано.
- форма Пеано.
2. y=f(x)=sinx, 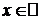 .
.
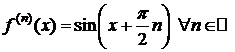 ,
,
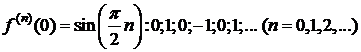 Þ
Þ
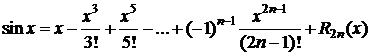 ,
,
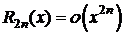 .
.
3.y=f(x)=cosx, 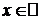 .
.
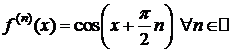 ,
, 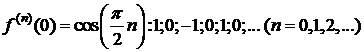 Þ
Þ
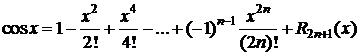 ,
,
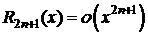 .
.
4. y=f(x)=ln(1+x), 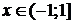 .
.
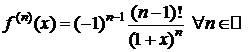 .
. 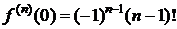 Þ
Þ
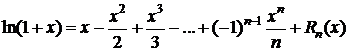 ,
,
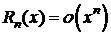 .
.
5. y=f(x)=(1+x)m, 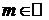 ,
, 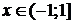 .
.
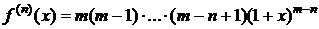 ,
, 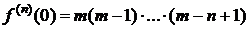 ,
,
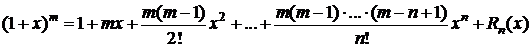 ,
,
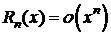 .
.
6. Пусть в случае 5 m=n 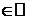 Þ
Þ 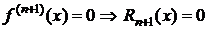 . Тогда
. Тогда
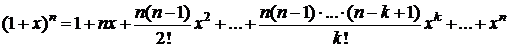 ,
,
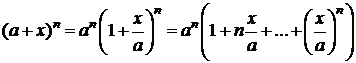 Þ
Þ
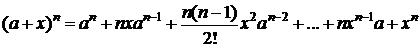 - бином Ньютона.
- бином Ньютона.
7. Пусть в случае 5 m=-1 Þ
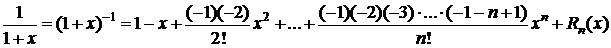 ,
,
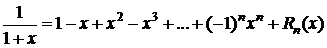 .
.
Положим здесь х=-х:
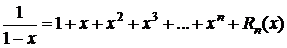 .
.
Пример.
D 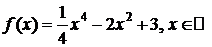
f ¢(x)=x3-4x, f ²(x)=3x2-4
f ¢(x)=0 при x1=0, x2=2, x3=-2
f ²(0)=-4 Þ x=0 – точка строго максимума, maxf(x)=f(0)=3
f ²(±2)=8 Þ x=±2 – точки строго минимума, minf(x)=f(±2)=-1. D
3. Нахождение наибольшего и наименьшего значений функции на отрезке
Пусть функция f(x) дифференцируема на отрезке [a;b]. Тогда она непрерывна на этом отрезке и, в силу II – й теоремы Вейерштрасса, достигает на нем наибольшего и наименьшего значений. Если функция имеет наибольшее значение на (a;b), то это – один из максимумов. Но функция может иметь наибольшее значение и на концах отрезка [a;b]. Аналогичные рассуждения – для минимума. Значит, для нахождения наибольшего и наименьшего значений функции на отрезке [a;b] надо:
1) найти все критические точки функции, принадлежащие отрезку [a;b];
2) вычислить значения функции в этих точках и на концах отрезка;
3) из полученных значений выбрать наибольшее и наименьшее.
4. Выпуклость функции
Пусть функция f(x) дифференцируема на <a;b>. Тогда существует касательная к графику функции f(x) в любой точке М(x;f(x)), xÎ<a;b>, причем эти касательные не параллельны оси Оу.

 Определение. Функция f(x) называется выпуклой вверх (вниз) на <a;b>, если график функции в пределах <a;b> лежит не выше (не ниже) любой из своих касательных.
Определение. Функция f(x) называется выпуклой вверх (вниз) на <a;b>, если график функции в пределах <a;b> лежит не выше (не ниже) любой из своих касательных.
Теорема 8. Пусть функция f(x) дважды дифференцируема на <a;b>. Тогда если f ²(x)³0 (f ²(x)£0) на (a;b), то функция выпукла вниз (вверх) на <a;b>.
Доказательство.
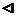 Пусть f ²(x)³0 "хÎ<a;b>. Зафиксируем произвольное х0Î(a;b). Докажем, что график функции в пределах (a;b) лежит не ниже касательной в точке М0(x0;f(x0)). Уравнение касательной:
Пусть f ²(x)³0 "хÎ<a;b>. Зафиксируем произвольное х0Î(a;b). Докажем, что график функции в пределах (a;b) лежит не ниже касательной в точке М0(x0;f(x0)). Уравнение касательной:
yкас.-f(x0)=f ¢(x0)(x-x0). (1)
Разлагая f(x) по формуле Тейлора для n=1 "хÎ(a;b), получим
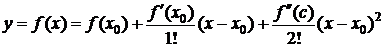 , х¹х0, х0<c<x (x<c<х0) (2)
, х¹х0, х0<c<x (x<c<х0) (2)
Вычтем (1) из (2):
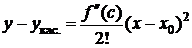 , сÎ(х0;х) (сÎ(х;х0)). (3)
, сÎ(х0;х) (сÎ(х;х0)). (3)
"хÎ(a;b) f ²(x)³0, сÎ(х0;х)Ì(a;b). Следовательно, f ²(с)³0.
Тогда из (3) следует y-yкас.³0 "хÎ(a;b), т. е. y³yкас. "хÎ(a;b). Следовательно, график функции в пределах (a;b) лежит не ниже касательной. Т. к. х0 - произвольная точка из интервала (a;b), то f(x) выпукла вниз на <a;b>. 
Пример.
D y=f(x)=x3, 
f ¢(x)=3x2, f ²(x)=6x
f ²(x)³0 при x³0 Þ на [0;+¥) функция выпукла вниз,
f ²(x)£0 при x£0 Þ на (-¥;0] функция выпукла вверх. D
5. Точки перегиба
Пусть f(x) определена и непрерывна в V(x0).
Определение.Точка x0 называется точкой перегиба функции f(x), если при переходе через эту точку меняется направление выпуклости функции f(x).
В примере х=0 – точка перегиба.
Теорема 9 (необходимое условие перегиба). Если в точке перегиба x0 функции f(x) вторая производная существует и непрерывна, то она в этой точке равна нулю.
Доказательство.
 Пусть в точке перегиба x0 существует непрерывная f ²(x0). В условиях теоремы для f ²(x0) возможны 3 случая.
Пусть в точке перегиба x0 существует непрерывная f ²(x0). В условиях теоремы для f ²(x0) возможны 3 случая.
1) f ²(x0)>0. Следовательно, т. к. f ²(x0) непрерывна, $V(x0), в которой f ²(x)>0, т. е. в точке x0 функция не меняет направления выпуклости. Значит, x0 не является точкой перегиба.
2) f ²(x0)<0. Следовательно, $V(x0), в которой f ²(x)<0. Значит, x0 не является точкой перегиба.
3) f ²(x0)=0. 
В точке перегиба вторая производная может не существовать.
Пример.
D 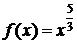 ,
, 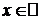 .
.
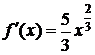 ,
, 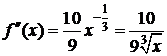 .
.
Следовательно, в точке х0=0 f ² не существует.
При x>0 f ²(x)>0 Þ на (0;+¥) функция выпукла вниз,
При x<0 f ²(x)<0 Þ на (-¥;0) функция выпукла вверх.
Значит, х0=0 - точка перегиба. D
Т. о., точками возможного перегиба являются те точки из области определения функции, в которых вторая производ
