Дифференцируемость функции нескольких переменных, частные производные, полный дифференциал

Функция называется дифференцируемой в данной точке, если ее полное приращение в этой точке может быть представлено в виде: 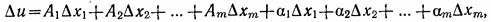, где А₁, А₂, …, А_m – некоторые не зависящие от ∆х₁, ∆х₂, …, ∆х_m числа, а α₁, α₂, …, α_m – бесконечно малые при 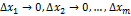функции, равные 0 при ∆х₁=∆х₂=…∆х_m=0.

Частная производная функции z=f(x,y) по х – предел отношения частного приращения функции по х к приращению Δх при Δх→0, если он существует и конечен: =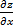

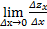
Частная производная функции z=f(x,y) по y- – предел отношения частного приращения функции по y к приращению Δy при Δy→0, если он существует и конечен:: =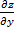

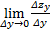
Полный дифференциал функции z=f(x,y) - главная линейная относительно 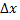и ∆у часть приращения функции ∆z в точке (х,у).

dz= 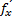(x,y)dx+ 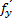(x,y)dy

Если функция f(x,y) определена в некоторой области D, то её частные производные f’x(x,y), f’y(x,y), тоже будут определены в той же области или её части. Будем называть эти производные производными I-ого порядка. Производные этих функций производными II-ого порядка.

; ;

; .

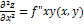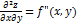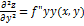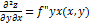Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков.

5. Экстремум функции двух переменных: необходимое и достаточное условия.

Понятие максимум, минимум, экстремум функции двух переменных аналогичны соответствующим понятиям функции одной независимой переменной. Пусть функция 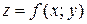определена в некоторой области 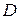, точка .

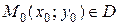Определение 2.1. Точка 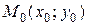называется точкой максимума 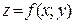, если существует такая 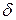-окрестность точки 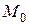, что для каждой точки 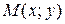, отличной от 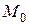, из этой окрестности выполняется неравенство

.

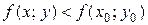Определение 2.2. Точка 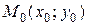называется точкой минимума 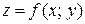, если существует такая 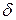-окрестность точки 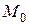, что для каждой точки 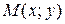, отличной от 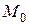, из этой окрестности выполняется неравенство

.

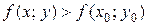Значение функции в точке максимум (минимум) называется максимум (минимум) функции. Максимум и минимум функции называют ее экстремумами.

Отметим, что, в силу определения, точка экстремума лежит внутри области определения функции; максимум и минимум имеют локальный (местный) характер; значение функции в точке 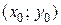сравнивается с ее значениями в точках, достаточно близких к 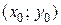. В области 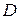функция может иметь несколько экстремумов или не иметь ни одного.

Рассмотрим условия существования экстремума функции (примем без доказательства).

Теорема 2.1 (необходимое условие экстремума). Если точка 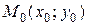является точкой экстремума функции 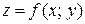, то 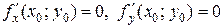или хотя бы одна из этих производных не существует.

Эта теорема не является достаточной для исследования вопроса об экстремальных значениях функции, но позволяет находить эти значения в тех случаях, в которых заранее уверены в существовании максимума или минимума. В противном случае требуется дополнительное исследование.

Например, функция 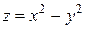имеет частные производные 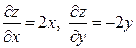, которые обращаются в нуль при 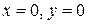. Но эта функция при указанных значениях не имеет ни максимума, ни минимума. Действительно, эта функция равна нулю в начале координат и принимает в как угодно близких точках от начала координат как положительные, так и отрицательные значения. Следовательно, значение нуль не является ни максимумом, ни минимумом.

Например, функция 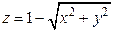имеет экстремум в точке 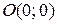, но не имеет в этой точке частных производных.

Определение 2.3. Точки, в которых хотя бы одна частная производная равна нулю или не существует, то такие точки называются критическими точками.

Если речь идет о точках, в которых частные производные первого порядка равны нулю, то такие точки называются стационарными точками.