Дифференцируемость функции
Определение 3.1.Функция 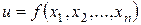 называется дифференцируемой в точке
называется дифференцируемой в точке 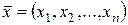 , если её полное приращение в этой точке может быть представлено в виде
, если её полное приращение в этой точке может быть представлено в виде
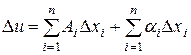 , (3.1)
, (3.1)
где 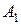 , …,
, …, 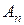 - некоторые числа, а
- некоторые числа, а 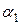 , …,
, …, 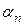 бесконечно малые функции при
бесконечно малые функции при 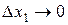 , …,
, …, 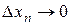 .
.
Теорема 3.1. (необходимое условие дифференцируемости). Если функция 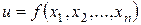 дифференцируема в точке
дифференцируема в точке 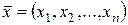 , то в этой точке она имеет частные производные по всем аргументам, причем
, то в этой точке она имеет частные производные по всем аргументам, причем 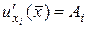 (
( 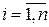 ), где
), где 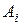 определяются из условия (3.1).
определяются из условия (3.1).
Доказательство. В силу (2.1) и (2.2) частное приращение 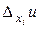 функции
функции 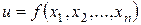 в точке
в точке 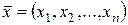 может быть получено из полного приращения
может быть получено из полного приращения 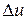 при
при 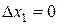 ,
, 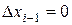 ,
, 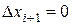 , …,
, …, 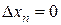 . Отсюда, согласно условию (3.1) дифференцируемости функции в точке
. Отсюда, согласно условию (3.1) дифференцируемости функции в точке 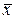 , ее частное приращение
, ее частное приращение 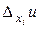 в этой точке можно представить в виде
в этой точке можно представить в виде 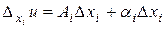 . В предположении
. В предположении 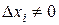 последнее равенство может быть переписано в виде
последнее равенство может быть переписано в виде 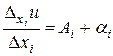 , что по свойству предела эквивалентно равенству
, что по свойству предела эквивалентно равенству 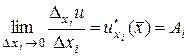 .
.
В силу теоремы 3.1 условие (3.1) дифференцируемости функции 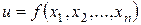 в точке
в точке 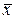 можно представить в следующей форме:
можно представить в следующей форме:
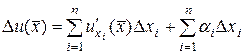 .
.
Теорема 3.2. (достаточное условие дифференцируемости). Если функция 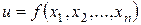 имеет частные производные по всем аргументам в некоторой окрестности точки
имеет частные производные по всем аргументам в некоторой окрестности точки 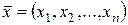 , причем все эти частные производные непрерывны в самой точке
, причем все эти частные производные непрерывны в самой точке 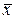 , то указанная функция дифференцируема в точке
, то указанная функция дифференцируема в точке 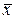 .
.
Доказательство теоремы 3.2 можно найти в [1] и [2].
Как частный случай определения 3.1 получаем
Определение 3.2. Функция 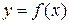 называется дифференцируемой в точке х, если ее приращение в этой точке может быть представлено в виде
называется дифференцируемой в точке х, если ее приращение в этой точке может быть представлено в виде
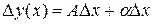 , (3.2)
, (3.2)
где А – некоторое число, а 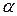 - бесконечно малая величина при
- бесконечно малая величина при 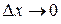 .
.
Теорема 3.3. (необходимое и достаточное условие дифференцируемости функции одной переменной). Функция 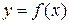 дифференцируема в точке х тогда и только тогда, когда в этой точке существует производная
дифференцируема в точке х тогда и только тогда, когда в этой точке существует производная 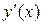 , причем
, причем 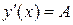 .
.
Доказательство. Пусть функция 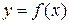 дифференцируема в точке х, т.е.
дифференцируема в точке х, т.е. 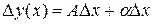 или при условии
или при условии 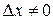
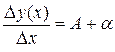 , или по свойству предела
, или по свойству предела 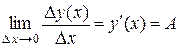 .
.
Таким образом, дифференцируемость функции одной переменной равносильна существованию производной этой функции. Функция 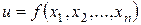 при
при 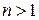 указанным свойством не обладает.
указанным свойством не обладает.
Теорема 3.4. Если функция 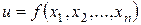 дифференцируема в точке
дифференцируема в точке 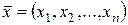 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
Доказательство. Если функция 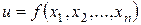 дифференцируема в точке
дифференцируема в точке 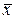 , то ее полное приращение в этой точке представимо в виде
, то ее полное приращение в этой точке представимо в виде
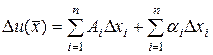 ,
,
где 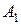 , …,
, …, 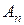 - некоторые числа, а
- некоторые числа, а 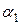 , …,
, …, 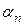 бесконечно малые функции при
бесконечно малые функции при 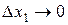 , …,
, …, 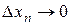 .
.
Переходя в последнем равенстве к пределу при 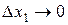 , …,
, …, 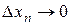 , получим
, получим 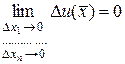 , что равносильно непрерывности функции
, что равносильно непрерывности функции 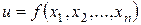 в точке
в точке 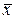 .
.
Обратное утверждение о том, что из непрерывности следует дифференцируемость, вообще говоря, неверно. Например, функция
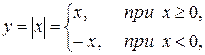
непрерывна в точке 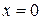 , так как в этой точке существуют правое и левое предельные значения функции, оба равные значению функции в точке
, так как в этой точке существуют правое и левое предельные значения функции, оба равные значению функции в точке 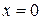 . Данная функция в точке
. Данная функция в точке 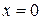 имеет правую производную
имеет правую производную
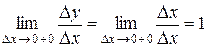
и левую производную
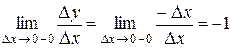 .
.
Но поскольку указанные производные не совпадают, функция 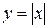 не имеет производной в точке
не имеет производной в точке 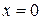 , и следовательно, по теореме 3.3 не дифференцируема (см. рис. 3.1).
, и следовательно, по теореме 3.3 не дифференцируема (см. рис. 3.1).
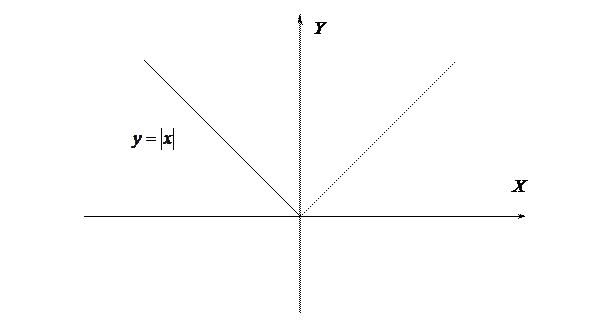
Рис. 3.1
