Разложение функции в степенные ряды

Теорема Абеля

Если степенной ряд (*) сходится в точке 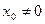, то он сходится и притом абсолютно, в интервале , т. е. при всяком x , удовлетворяющем условию .

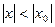Доказательство:

Заметим, что вследствие сходимости ряда 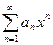его общий элемент 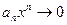. Поэтому все элементы этого ряда ограничены в совокупности, т.е. существует М>0, такое, что при всяком n . Запишем ряд (*) так

и составим ряд их абсолютных величин элементов этого ряда:

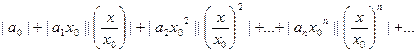
В силу установленного неравенства каждый элемент здесь меньше соответствующего элемента геометрической прогрессии со знаменателем :

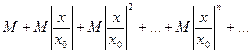
Если 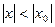, то 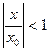и прогрессия сходится, поэтому сходится ряд из абсолютных величин, а значит, абсолютно сходится сам ряд (*). Теорема доказана.

Несмотря на то, что 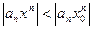нельзя сразу воспользоваться признаком сравнения, поскольку в условиях теоремы не сказано, что ряд в самой точке 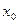сходится абсолютно.

Следствие

Если степенной ряд (*) расходится при 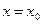, то он расходится и при всяком х, большем по абсолютной величине 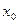, то есть при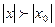

Область сходимости степенного ряда

Здесь возможны три случая:

1) Область сходимости состоит только из одной точки х=0, то есть ряд расходится для всех значений х, кроме х=0. Пример

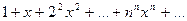
Если х фиксировано и х не равно 0,то, начиная с достаточно большого n, будет 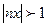, откуда вытекает неравенство 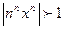, означающее, что общий элемент ряда не стремится к нулю.

2) Область сходимости состоит из всех точек оси ОХ, то есть ряд сходится при всех значениях х. Пример

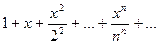
Для любого х, начиная с достаточно большого n, будет 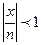, так как

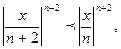и т.д.

Начиная с номера n, элементы ряда по абсолютной величине будут меньше элементов сходящейся геометрической прогрессии. Следовательно, при любом х ряд сходится.

3) Область сходимости состоит более чем из одной точки оси ОХ, причем есть точки оси, не принадлежащие области сходимости. Пример

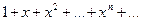
Это геометрическая прогрессия со знаменателем х. Ряд сходится при |x|<1 и расходится при .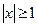

В этом случае на числовой оси наряду с точками сходимости ряда имеются и точки его расходимости.

Из теоремы Абеля и ее следствия вытекает, что все точки сходимости расположены от начала координат не дальше, чем любая из точек расходимости. Точки сходимости будут целиком заполнять некоторый интервал с центром в начале координат.

Таким образом

Для каждого степенного ряда, имеющего как точки сходимости , так и точки расходимости, существует такое положительное число R, что для всех х по модулю меньшим R ( 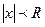), ряд абсолютно сходится, а для всех |x|>R ряд расходится. При x=R и x=-R различные варианты:

А) ряд сходится в обеих точках.

Б) ряд сходится в одной из точек.

В) ряд расходится в обеих точках.

Определение

Радиусом сходимости степенного ряда (*) называется такое число R, что для любых х, |x|<R, степенной ряд сходится, а для всех х, |x|>R, расходится. Интервал (-R,R) называется интервалом сходимости.

Считаем, что если ряд расходится для любого х, кроме х=0, R=0.

Если ряд сходится при всех х, то считаем 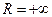или .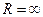

Для ряда 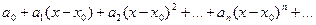центр интервала сходимости в точке 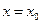( а не х=0) и интервал сходимости .

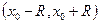Способ отыскания радиуса сходимости степенного ряда

Отметим, что для нахождения радиуса сходимости можно исследовать ряд, составленный из абсолютных величин элементов исходного ряда, то есть

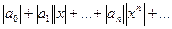(**) так как интервалы сходимости ряда (*) и ряда (**) совпадают. К ряду (**) применим признак Даламбера. 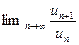будет содержать |x| или степень |x|

Для тех значений х, при которых получаемый предел меньше 1, ряд сходится, а для тех, при которых x>1, ряд расходится. Отсюда следует, что значения |x|, при которых этот предел равен 1, и будет являться радиусом сходимости ряда.

Может случиться, что найденный предел при всех х будет равен 0. Это означает, что ряд (*) сходится при всех х и .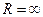

Наоборот, если для любых х кроме х=0 предел равен бесконечности, то ряд будет везде расходиться, кроме х=0, то есть R=0.

Примеры

1) Найти радиус сходимости ряда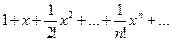

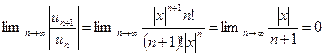, то есть для всякого х ряд сходится .

2) Найти радиус сходимости ряда

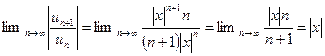
Если |x|<1 - ряд сходится

Если |x|>1 – ряд расходится

При х=1 получаем гармонический ряд, который расходится.

При х=-1 ряд 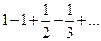сходится условно.

3) Найти радиус сходимости ряда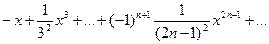

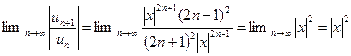, то есть R=1

При |x|<1 – ряд сходится

При |x|>1 – ряд расходится

При |x|=1 – ряд сходится абсолютно.

4) Найти радиус сходимости ряда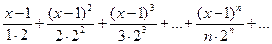

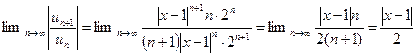
Если 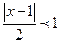ряд сходится, то есть при -2<x-1<2. Получаем интервал сходимости (-1,3) с центром х=1.

Свойства степенных рядов

Рассмотрим степенной ряд (*), имеющий радиус сходимости R (конечный или бесконечный).

Сумма ряда S(x) – есть функция, определенная внутри интервала сходимости, а также в том из концов интервала, где ряд сходится. Предварительно рассмотрим леммы.

Лемма 1

Степенной ряд правильно сходится в любом отрезке [-b,b], целиком лежащем в интервале сходимости (-R,R)

Доказательство

Выберем точку , так чтобы было

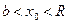
__________(____[______________]______)_______ X

-R -b b R

Она лежит в интервале сходимости и по теореме Абеля числовой ряд 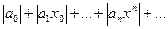сходится. Для всех точек 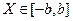имеем 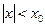, и следовательно 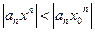. Последнее неравенство и означает, что ряд (*) правильно сходится в отрезке [-b,b].

Лемма 2

Степенной ряд, составленный из производных элементов ряда (*) имеет тот же радиус сходимости, что и данный ряд.

Доказательство

Ряд из производных имеет вид 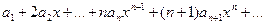(**). Предположим, что предел отношения 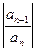существует, и применим для отыскания радиусов сходимости признак Даламбера:

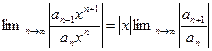для (*)

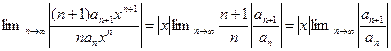
Равенство пределов отношения последующего элемента к предыдущему для обоих рядов, показывает, что их радиусы сходимости равны.

Следует отметить, что на конце интервала сходимости ряд (**) может расходиться и тогда, когда ряд (*) сходится.

Например

Ряд

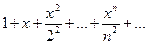
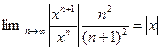при 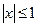ряд сходится.

Ряд производных

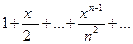при х=1 – гармонический ряд, который расходится.

Если теперь составить ряд из производных ряда (**), то он опять будет иметь тот же радиус сходимости и т.д. Таким образом, все степенные ряды, получающиеся последовательным дифференцированием ряда (*) имеют один и тот же радиус сходимости и по лемме 1 правильно сходятся в любом интервале, целиком принадлежащем интервалу сходимости.

Свойство 1

Сумма степенного ряда есть функция, непрерывная в интервале сходимости ряда:

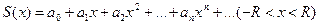
Заметим, что в том конце интервала, где степенной ряд сходится, его сумма S(x) остается односторонне непрерывной (изнутри интервала сходимости).

Замечание

Следует учитывать одно обстоятельство, которое может иногда привести к недоразумению.

Возьмем геометрическую прогрессию, сходящуюся при |x|<1

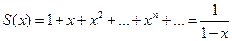
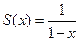определена всюду, кроме точки х=1. Тем не менее, следует твердо помнить, что S(x) является суммой ряда только при |x|<1; При |x|>1 ряд расходится и о его сумме говорить нельзя.

Свойство 2

Степенной ряд можно поэлементно интегрировать в интервале сходимости

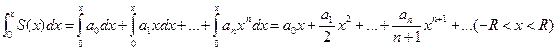. Получившийся степенной ряд имеет тот же радиус сходимости, что и данный.

Свойство 3

Степенной ряд можно поэлементно дифференцировать в интервале сходимости

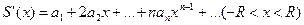
далее

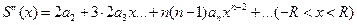
и так далее.

Итак, степенной ряд в интервале его сходимости можно поэлементно дифференцировать любое число раз, при этом радиусы сходимости получающихся рядов остаются прежними.

Разложение функции в степенные ряды

Известно, что сумма степенного ряда в интервале сходимости этого ряда является непрерывной и бесконечное число раз дифференцируемой.

Обратный вопрос?

Когда можно утверждать, что заданная функция f(x) является суммой некоторого степенного ряда?

Из свойств степенных рядов следует, что эта функция должна быть бесконечное число раз дифференцируема (но это условие не достаточное).

Остается вопрос установить, какие функции и в каких интервалах можно представить в виде суммы степенных рядов.

В дальнейшем, если заданную функцию f(x) можно представить в виде суммы некоторого степенного ряда, то говорят, что функция f(x) разложена в степенной ряд.

Важность такого разложения очевидна, так как, получаем возможность приближенно заменить функцию суммой нескольких первых элементов степенного ряда, то есть многочленом. Вычисление значений многочленов – простейшие арифметические операции. Важно, что можно оценить точность получаемых приближенных значений.

Замена функции таким простым выражением, как многочлен, оказывается очень удобной в различных вопросах мат. анализа: при вычислении интегралов, решении дифференциальных уравнений и т.д.

Итак, предположим, что функция f(x) бесконечное число раз дифференцируема в окрестности некоторой точки 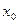. Допустим, что ее можно представить в виде суммы степенного ряда, сходящегося в каком-то интервале, содержащем точку .

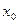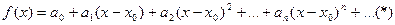, где 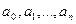- пока неопределенные коэффициенты. Покажем, как пользуясь свойствами степенных рядов можно найти эти коэффициенты по известным значениям функции f(x) и ее производных в точке .

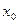Положим в (*) 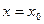. Получаем 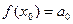. Продифференцируем степенной ряд

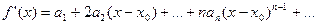и снова положим 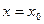. Получим 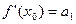. Последующее дифференцирование дает 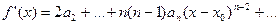При 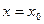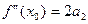, то есть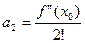

После n-кратного дифференцирования получает 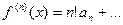Все остальные элементы содержат множитель 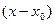. При 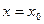получим 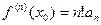, то есть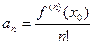

Таким образом, находятся последовательно все коэффициенты разложения (*). Подставляя найденные выражения в равенство (*) получим ряд 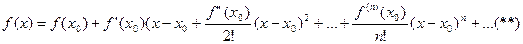. Такой ряд называется рядом Тейлора функции f(x).

Определение

Рядом Тейлора функции f(x) в окрестности точки 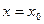называется степенной ряд (**) относительно разности 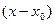, коэффициенты которого выражаются через функцию f(x) и ее производные в точке 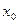. Эти коэффициенты называются коэффициентами Тейлора функции f(x) в точке .

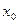Установили, что если функцию можно разложить в степенной ряд по степеням разности 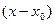, то этот ряд обязательно является рядом Тейлора этой функции.

Замечание

Все рассуждения сделаны в предположении, что функция f(x) может быть разложена в степенной ряд. Если этого не предполагать, а просто считать функцию f(x) бесконечное число раз дифференцируемой и составить для нее ряд Тейлора, то ниоткуда не следует, что этот ряд сходится при значениях х, отличных от 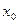.