Метод Фурье для уравнений гиперболического типа
Разберем простейшее уравнение, описывающее колебание струны, закрепленной на концах, без воздействия внешних сил.
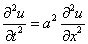 (1)
(1)
при начальных условиях
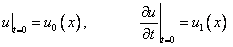 (2)
(2)
и граничных условиях
 . (3)
. (3)
Пояснение:
Начальное условие 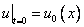 означает, что в нулевой момент времени струна имеет форму
означает, что в нулевой момент времени струна имеет форму 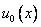 .
.
Начальное условие 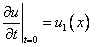 означает, что в нулевой момент времени скорости точек струны равны
означает, что в нулевой момент времени скорости точек струны равны 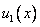 .
.
Граничные условия 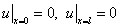 означают, что концы струны жестко закреплены.
означают, что концы струны жестко закреплены.
Метод Фурье, или метод разделения переменных основывается на том, что решение ищется в виде
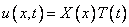 -
-
произведения двух функций, одна из которых зависит только от 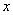 , а другая только от
, а другая только от 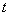 .
.
1) Найдем частные решения уравнения (1), не равные тождественно нулю и удовлетворяющие граничным условиям (3).
Подставим 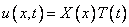 в исходное уравнение
в исходное уравнение 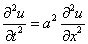 .
.
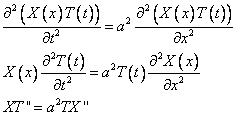
Поделим обе части полученного равенства на 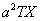
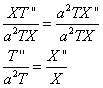
Пояснение: Получено равенство, левая часть которого зависит только от 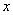 , а правая часть – только от
, а правая часть – только от 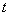 . Функции разных переменных могут быть равны между собой только в том случае, если они равны какому то числу, константе, обозначается эта константа
. Функции разных переменных могут быть равны между собой только в том случае, если они равны какому то числу, константе, обозначается эта константа 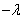 .
.
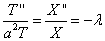
Получены два уравнения:
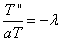 и
и 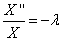 , или, после преобразований
, или, после преобразований
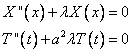
Рассмотрим первое из них. Необходимо найти нетривиальные (не равные тождественно нулю) решения этого уравнения, удовлетворяющие условиям
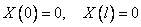 .
.
Замечание: Это есть граничные условия  .
.
Это задача Штурма-Лиувилля. Однако её может решить любой, изучивший курс дифференциальных уравнений.
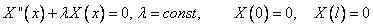 (4)
(4)
- линейное уравнение с постоянными коэффициентами. Составляем характеристическое уравнение:
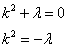
Замечание: Не вдаваясь в подробности: 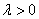 .
.
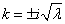
Общее решение уравнения (4):
 .
.
Определим значение коэффициентов 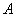 и
и 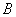 из условий
из условий 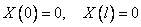 .
.
1) 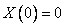
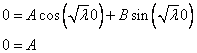
Подставляем в общее решение и получаем: 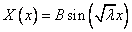 .
.
2) 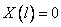
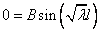
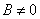 , иначе решением будет только
, иначе решением будет только 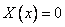 .
.
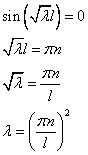
- это, в зависимости от 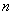 – собственные значения задачи.
– собственные значения задачи.
Т.к. выполнение условий не зависит от коэффициента 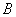 , то примем его значение равным 1.
, то примем его значение равным 1.
Итак, нетривиальными решениями уравнения (4) являются функции
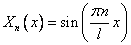 .
.
Решим уравнение 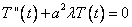 , причем уже известно, что
, причем уже известно, что 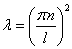 .
.
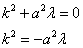
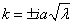
Общее решение уравнения (4):
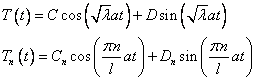 .
.
Возвращаемся к поставленной задаче (1):
Функции
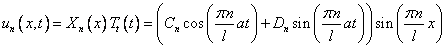
Являются частными решениями уравнения (1), удовлетворяющими условиям (3) .
Т.к. уравнение (1) линейно и однородно, то сумма частных решений
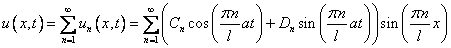
также является решением.
Теперь стоит разобраться с начальными условиями : 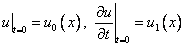 .
.
1) 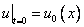
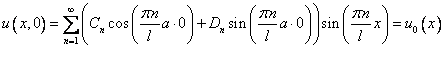
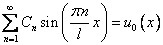 (5)
(5)
2) 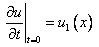
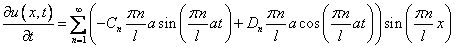
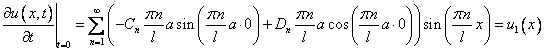
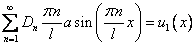 (6)
(6)
Замечание: Из теории рядов Фурье известно, что произвольная, кусочно-непрерывная и кусочно-дифференцируемая функция 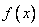 , заданная в промежутке
, заданная в промежутке 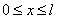 , разлагается в ряд Фурье
, разлагается в ряд Фурье
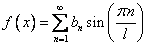 , где
, где 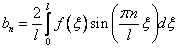 .
.
Можно заметить, что (5) и (6) есть разложения в ряд Фурье функций 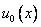 и
и 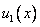 , а
, а 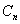 и
и 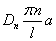 – коэффициенты этих разложений, значит, их можно определить по формулам
– коэффициенты этих разложений, значит, их можно определить по формулам
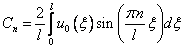 и
и 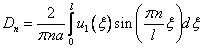 (7).
(7).
Вывод:
Ряд 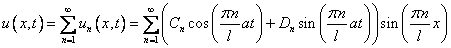
с коэффициентами
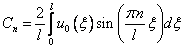 и
и 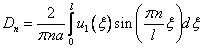
является решением задачи (1) – (3).
3.2
