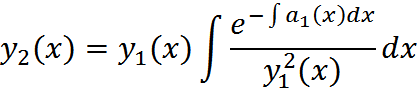Линейные ДУ высших порядков. Т. о существовании и единственности решения задачи Коши. Т. о св-ве решений ЛОДУ

Ур-е 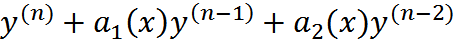+ …+ 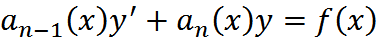наз-ся ЛНДУ n-го порядка.

Если f(x)=0, то ур-е наз-ся ЛОДУ n-го порядка. З.Коши для ЛДУ определяется начальными условиями:

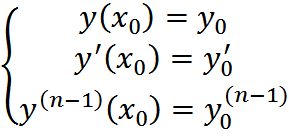
Теорема существования и единственности решения задачи Коши.

Если все коэф-ты t wx:val="Cambria Math"/><w:i/><w:sz w:val="32"/><w:sz-cs w:val="32"/></w:rPr><m:t>Нћn</m:t></m:r><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="32"/><w:sz-cs w:val="32"/></w:rPr><m:t> </m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 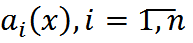и f(x) непр-ы на [a,b], то на всем этом отрезке сущ-т единственное реш--е з.Коши.

Теорема о свойстве решений линейных однородных дифференциальных уравнений.

1) Если 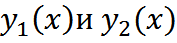явл-ся реш-ми ЛОДУ, то ф-я 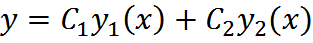также яв-ся реш-м ЛОДУ при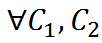

2) Если комплекснозначная ф-я 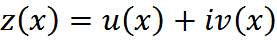яв-ся реш-м ЛОДУ, то ф-и 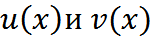в отдельности также явл-ся реш-и ЛОДУ.

Линейная независимость функций. Определитель Вронского

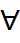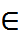Ф-и y₁, y₂, …, y_n наз-ся линейно зависимыми на (a,b), если сущ-т такие const α₁, α₂, …, α_n, при кот-х выпол-ся α₁у₁(х)+ α₂у₂(х)+…+ α_nу_n(х)=0, x (a,b).

Если это равенство выполняется лишь при α₁=α₂=…=α_n=0, то ф-и у₁, у₂, …, у_n наз-ся линейно независимыми на (a,b).

ТЕОРЕМА: Ф-и у₁(х) и у₂(х) линейно зависимы на (a,b) только тогда, когда 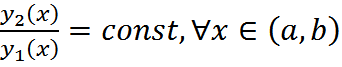; и линейно независимы, если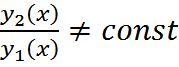

Для системы из n ф-й вопрос о линейной зависимости реш-ся с помощью определителя Вронского:

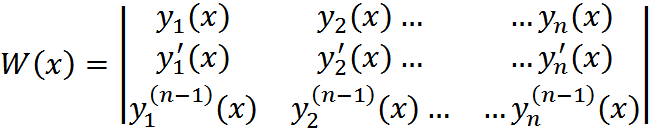
ТЕОРЕМА: Если у₁, у₂, …, у_n линейно зависимы на (a, b), то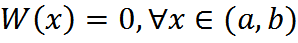

Структура общего решения ЛОДУ высших порядков

ТЕОРЕМА:

1.Любое ЛОДУ n-го порядка имеет ровно n линейно независимых реш-й

2.Общее решение ЛОДУ имеет вид:

у=С₁у₁(х)+С₂у₂(х)+…+С_ny_n(x), где С₁, С₂, …, С_n – произвольные const

Определение: Любая система n линейно независимых реш-й ЛОДУ наз-ся фундам-ой системой реш-й (ФСР) этого ур-я.

Формула Лиувилля для определителя Вронского, построенного на ФСР ЛОДУ

ТЕОРЕМА (Формула Лиувилля): Если у₁(х), у₂(х)–ФСР ЛОДУ 2пор-а с перем-и коэф-ми

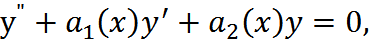
то опред-ль Вронского, состав-ый из этих ф-й имеет вид: 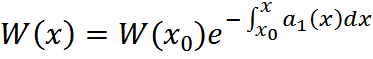, где х₀ – произвольное значение, взятое из обл. непре-ти коэф-в а₁(х) и a₂(х)

Следствия т.к. 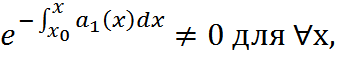то

_1.если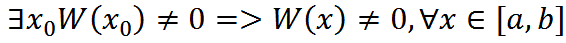

_2.если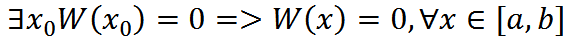

Теорема об отыскании второго решения ЛОДУ 2-го порядка по известному первому решению

Если известно одно частное реш-е у₁(х) ЛОДУ с переменными коэф-ми

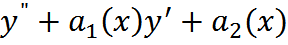y=0, то второе реш-е этого ур-я у₂(х) из ФСР нах-ся по ф-ле: