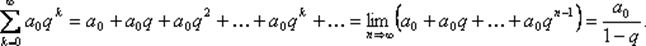ДУ с разделяющимися переменными

Ур-е вида (4) реш по схеме:

d(y)/d(x)=f(x)gy

d(y)/g(x)=f(x)d(x)

M(x)d(x)/K(x)=L(y)d(y)/N(y)

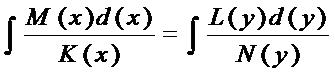
5) y’=g(y/x) однородное ДУ 1го порядка(ф-ция вида f(αx,αy)=α^kg(x,y) наз однор ф-ция k-того порядка,αЄR)

Реш с помощью подстановки

z=y/x y=zx y’=z’_xx+z

z’x+z=g(z) d(z)/(g(z)-z)=d(x)/x

6) y’=f(ax+by) приводится к ур-ю вида (4) путем замены z=ax+by

21. Линейные ДУ 1-го порядка

Уравнение вида ,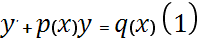

где p(x) и q(x) – заданные функции, назыв. линейным дифференциальным уравнением 1-го порядка. Если в ур-нии 1 правая часть тождественно равна 0, то получим ур-ние вида 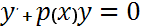(2) (однородное линейное ДУ 1-го порядка)

2—решают как ур-ние с раздел. переменными

1—решают с помощью подстановки:

,

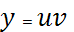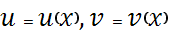
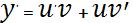
(u’v+uv’)+p(x)uv=q(x)

u’v+u(v’+p(x)v)=q(x)

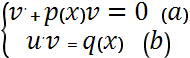
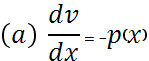
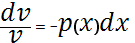
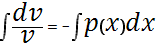
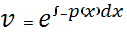
Подставляем во 2-ое уравнение системы (b):

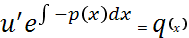
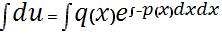
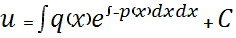
Общее решение уравнения :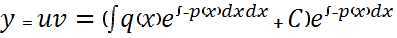

22. Линейные ДУ 2-го порядка.

Вид:

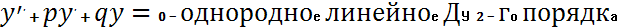
Методика решения:

Уравнение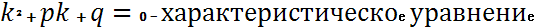

Общее решение зависит от корней характеристического.

a) D<0, 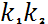, тогда решение имеет вид:

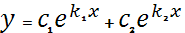
b)D=0, =>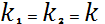

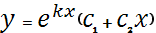
c) D<0, =>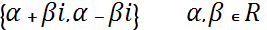

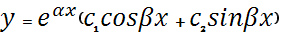
23. Линейные однородные ДУ 2 порядка с постоянными коэфф-ми. Их нахождение.

Обыкн ДУ 2 порядка с пост.коэфф. имеет вид:

(1) y``+py`+qy=r(x) p,q принадл. R, r(x) – функция

Если r(x) =0, то

(2) y``+ py`+qy=0 – однор.лин.ДУ с пост.коэфф.

Ур-е вида (3) 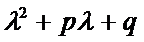=0 – характерист.ур-е (1) и(2) Стр-ра общего решения ур.(2) определяется корнями квадр.ур-я. (3)

Возможны 3 случая

1. кв.ур-е имеет разные корни α1 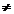α2, D>0 тогда общее решение:

y=C1 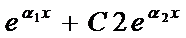C1, C2 прин.R

2. корни кв.ур. кратные, т.е. α1= α2=α ; D=0

y= 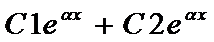C1, C2 прин.R

3. корни комплексно сопряженные : λ1= α-βi; λ2= α+βi;

y= C1 C1, C2 прин.R

24. Лин неоднор ДУ 2-го порядка с пост коэфф-ми.

Рассмотрим уравнение y´´+py´+qy=r(x) /где p,q ? R , r(x)-функция. которое имеет вид y=yO+yЧ, где

yO-общее решение уравнения y´´+py´+qy =0

yЧ-частное решение уравнения y´´+py´+qy=r(x) , которое зависит от вида правой части,т.е r(x)

Рассмотрим некоторые частные случаи:

1) r(x)=Pn(x) ,где Pn(x) – многочлен степени «n»

В этом случае решение yЧ ищут из уравнения к²+pк+q=0 в виде:

• yЧ=Qn(x) при q≠0

• yЧ=x Qn(x) q=0, p≠0

• yЧ=x² Qn(x) q=p=0

2) r(x)=а 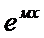где а,м ? R , а,м =соnst

Вид частного решения следущее:

• yЧ=А 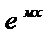если «м» не явл корнем Ур-я к²+pк+q=0

(корни некратные,некомплексные)

• yЧ=Аx 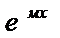если «м» –простой корень ур-я к²+pк+q=0

•yЧ=Аx² 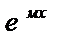если «м»-кратный корень Ур-я к²+pк+q=0

3) r(x)=acosmx+bsinmx где a,b,m=const

• yЧ= Acosmx+Bsinmx при условии что p²+(q-m²)≠0

• yЧ= x(Acosmx+Bsinmx) если p²+(q-m²)=0, p=0,q= m²

25.Числовой ряд и его сходимость.

Пусть задана бескон послед-ть чисел …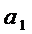

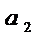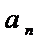
Тогда 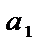+ +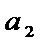… +…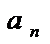= 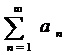(1) наз числовым рядом, а числа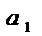 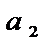-члены ряда, 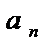-общий член ряда.

Сумма ряда. Примеры сходящихся и расходящихся рядов. Гармонический ряд (док-во его расходимости).

Сумма вида =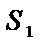

= + = +

= + +… = +

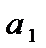
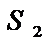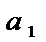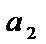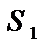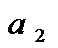
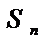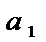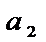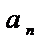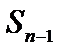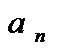
Называется частичными суммами ряда 1,

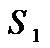
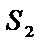
а последовательность 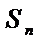(2) называется последовательность частичных сумм ряда (1)

Ряд (1) наз сход,если сх-ся посл-ть его частичных сумм(2)

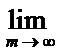
т.е если 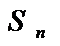=S При этом число S называется суммой ряда (1)

А если 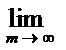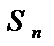= 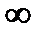или не сущ то ряд (1) наз расход.

Примеры рядов:

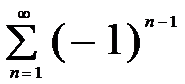• расходится

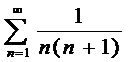• сходится

Ряд вида 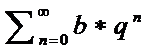- геом.прогрессия,ряд сход.если 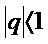и его сумма S=b/1-q,если 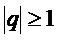ряд расх.

Свойства сходящихся рядов

Свойства-1. Если ряд u₁+u₂+u₃+….u_n+…= 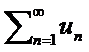(1) сход(расх.). И его сумма-S то сход(расх если с не равно 0) ,также и ряд 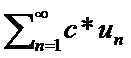и его сумма c*S.

2.Если ряд (1) и ряд 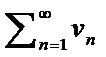их суммы S1 и S2 соответственно ,то сход и ряды 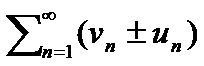и их суммы равны S1+S2.

3.Если к ряду (1) прибавить или отнять от него конечное число членов, то получим ряд и ряд (1) сход или расх одновременно. Ряд u_n+1+u_n+2+…= 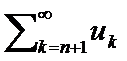обознач. Rn-остаток ряда (1),если ряд (1) сход. то его остаток стрем. к 0 при n стрем. к бесконечн.( 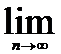Rn=0).

Необход.признак сходимости- если ряд(1) сход. то общий член этого ряда стрем к 0 ( 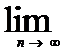a_n=0) Док-во: 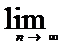u_n= 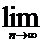(Sn-S_n-1)=0. Данный признак –не явл-ся достаточным(например гарм. ряд расх но u_n= 1/n стрем. к 0).

Док-во расх-ти гармонического ряда по Коши: f(x)=1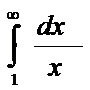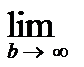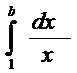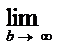/x = ; = (lnx) 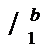= 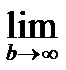(lnB*0),где lnB→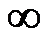

Ряд 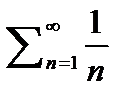гармонический и он всегда расход

Так называется ряд (бесконечная сумма), члены которого образуют геометрическую прогрессию с первым членом а0 и знаменателем прогрессии, равным q.

Если |q| < 1, то существует предел суммы n первых членов этой прогрессии при неограниченном увеличении количества этих членов n: