Глава 8. Несобственные интегралы

Глава 8. Несобственные интегралы

В предыдущей главе при построении теории определенного интеграла явно или неявно предполагались следующие ограничения:

1. отрезок 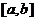имеет конечную длину;

2. подынтегральная функция 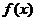ограничена.

Определенные интегралы, построенные при этих ограничениях, называются «интегралами в собственном смысле», или, короче, «собственными интегралами».

Сейчас мы будем отказываться от этих ограничений, и построенные интегралы называются «интегралами в несобственном смысле», или просто «несобственными интегралами».

Несобственные интегралы первого рода

Пусть

1. функция 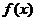определена на отрезке ;

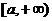2. 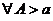существует .

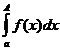Произведем теперь предельный переход 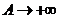. Тогда 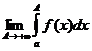называется несобственным интегралом первого родаи обозначается символом :

= .

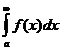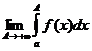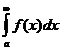Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится(или: существует).Если этот предел равен бесконечностиили вообще не существует, то говорят, что несобственный интеграл расходится(или: не существует).

Совершенно аналогично определяются и следующие несобственные интегралы первого рода:

,

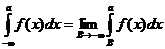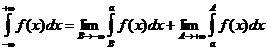(а - любое).

Простейшие свойства несобственных интегралов первого рода

Рассмотрим простейшие свойства несобственных интегралов первого рода.

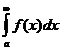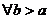1. Если сходится , то сходится и 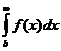. Наоборот, если 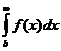сходится и существует 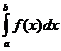, то сходится и 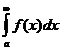. При этом верно соотношение

.

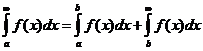Доказательство. Пусть 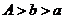. Тогда имеем

.

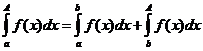Сделаем предельный переход А®+¥:

.

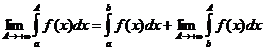Так как предел слева существует, то существует и предел справа и 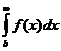сходится и соотношение принимает вид

.

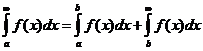Подумайте сами, что надо изменить в предыдущей фразе, чтобы доказать обратное утверждение.

2. Если 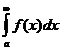сходится, то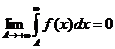

Доказательство.

Согласно предыдущему пункту

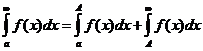
Отсюда

.

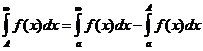Делая предельный переход А®+¥, получаем

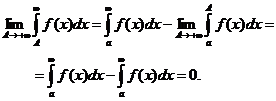
3. Если сходятся 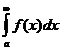и 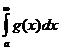, то сходится также и 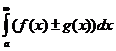и верно соотношение

= ± .

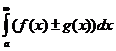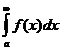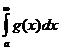Доказательство. Имеем

.

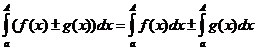Делая предельный переход А®+¥, получаем

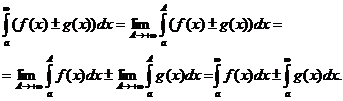
4. Если сходятся 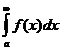и с - константа, то сходится и 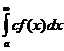и верна формула

.

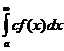
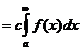Доказательство. Имеем

.

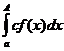
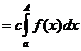Делая предельный переход А®+¥, получаем

.

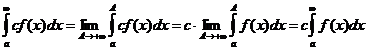Практический признак сходимости.

Пусть 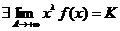, 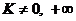. Тогда 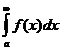сходится при 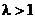и расходится при .

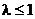(Заметим, что вопрос о том, как же находить l, остается на данном этапе открытым).

Доказательство.

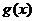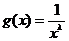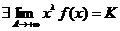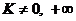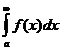Возьмем функцию в виде . Тогда условие теоремы 3 примет вид , и сходится или расходится одновременно с интегралом 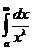.Рассмотрим поэтому вопрос о сходимости этого интеграла.

1. Пусть 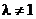. Тогда

.

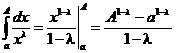Будут два варианта:

а) 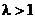. В этом случае 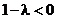, поэтому 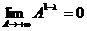и

,

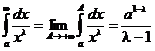так что 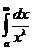сходится.

б) 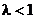. В этом случае 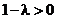, поэтому 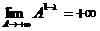и

,

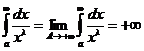так что 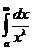расходится.

2. 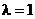. Тогда

,

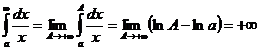так что 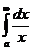расходится.

Таким образом, 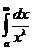сходится при 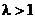и расходится при 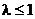. По теореме 2 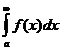также сходится при 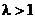и расходится при .<

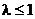Все упирается в нахождение величины l. Как это делать - будет разобрано на практике.

Признак Больцано-Коши

Для того, чтобы интеграл 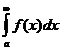сходился необходимо и достаточно, чтобы выполнялось условие

.

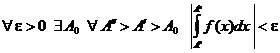Доказательство.

Снова рассмотрим функцию 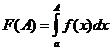. По признаку Больцано-Коши, для существования конечного предела 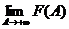необходимо и достаточно выполнение условия

.

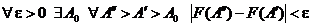Но в нашем случае

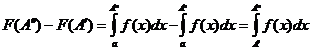
и поэтому признак Больцано-Коши принимает форму, указанную в формулировке теоремы.

Следствие. Если сходится 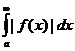, то сходится и .

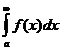Доказательство.

По признаку Больцано-Коши

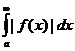сходится Þ .

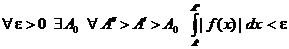(Обратите внимание, что написано так 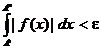, а не так 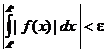; интересно, почему отсутствует знак модуля вокруг интеграла?).

Но тогда 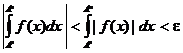и мы получаем, что

,

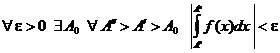откуда, по тому же самому признаку Больцано-Коши следует, что 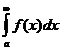сходится. <

Определение.Если 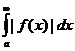сходится, то интеграл 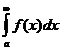называется абсолютно сходящимся (или: интеграл сходится абсолютно). Если же 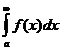сходится, но 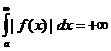, то интеграл 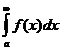называется неабсолютно сходящимся (или: интеграл сходится не абсолютно).

Вообще говоря, a priori не очевидно, что неабсолютно сходящиеся интегралы существуют вообще. Например, оказывается, что когда речь идет о плоскости и так называемых двойных интегралах, неабсолютно сходящихся интегралов не существует, и все двойные интегралы сходятся только абсолютно. Но в одномерном случае такие интегралы существуют, и ниже будет приведен пример такого интеграла.

Признак Больцано-Коши не является «рабочим» признаком, им не проверяется вопрос сходимости какого-то конкретного интеграла. Но на его основе строятся рабочие признаки, два из которых и будут рассмотрены ниже. Но, прежде чем перейти к их изучению, приведем без доказательства одну теорему, которая называется

Вторая теорема о среднем. Пусть

1. функция 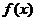интегрируема на отрезке ;

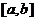2. функция 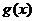монотонна и ограничена на этом отрезке.

Тогда существует точка 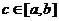, такая, что

.

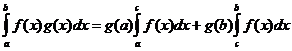Доказывать эту теорему мы не будем.

А теперь перейдем к изучению рабочих признаков сходимости несобственных интегралов.

Признак Дирихле.

Пусть

1. ;

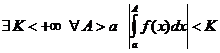2. при 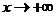функция 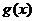монотонно убывает до нуля (запись: ).

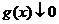Тогда 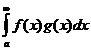сходится.

Доказательство.

1. Из первого ограничения теоремы 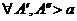имеем

.

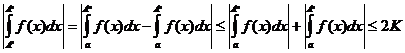2. Из второго ограничения теоремы имеем

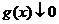Þ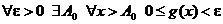

3. Возьмем любые 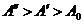. Тогда, используя вторую теорему о среднем, получим

.

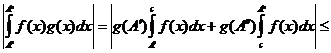
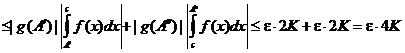Так как e сколь угодно мало, то, по признаку Больцано-Коши, 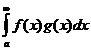сходится.

Следствие.Если 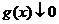, то сходятся следующие интегралы:

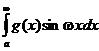(при любых значениях w) и 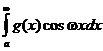(при w ¹ 0)

Доказательство.

Пусть 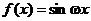или 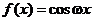. Тогда имеем

,

,

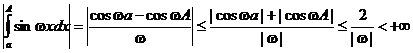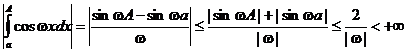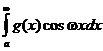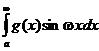если w ¹ 0. Поэтому, по признаку Дирихле, при w ¹ 0 интегралы и сходятся. Последний интеграл сходится и при w = 0 (он просто равен нулю). <

Теперь мы можем рассмотреть

пример неабсолютно сходящегося интеграла.

Таким интегралом является 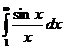. Так как при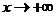 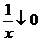, то этот интеграл сходится по признаку Дирихле.

Рассмотрим теперь 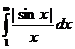. Из достаточно очевидного неравенства

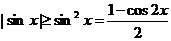
получаем

,

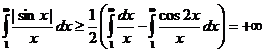так как 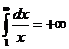(см. практический признак сходимости), а 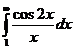сходится по тому же признаку Дирихле. Поэтому 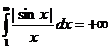и 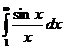сходится неабсолютно.

Признак Абеля.

Пусть

а) функции f (x) и g(x) определены на [a, +¥);

б) интеграл 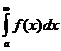сходится (не обязательно абсолютно!);

в) функция g(x) монотонна и ограничена.

Тогда интеграл 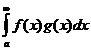сходится.

Доказательство.

Имеем

1. 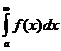сходится Þ ;

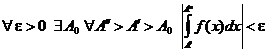2. функция 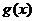ограничена Þ .

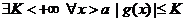3. В силу монотонности функции 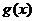можно снова воспользоваться второй теоремой о среднем. Получаем, что для любых любые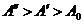

,

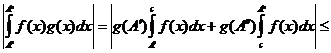
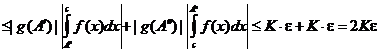и, по признаку Больцано-Коши, 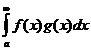сходится. <

Интегрирование по частям

Пусть функци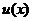и и 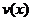непрерывны на промежутке 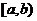и точка b является особой точкой по крайней мере для одной из них. Тогда, вспоминая формулу интегрирования определенных интегралов по частям, получим

.

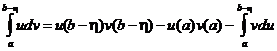Сделаем предельный переход 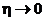. Переменная h есть в трех слагаемых. Если существуют два предела, то существует и третий, и мы получим

,

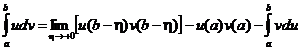что является формулой интегрирования по частям в несобственных интегралах.

Для несобственных интегралов первого рода она принимает вид

.

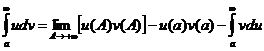Вывод аналогичен.

Замена переменных

Теорема. Пусть

1. 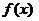определена на 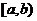(b - особая точка);

2. 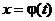, где на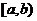 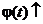и существует непрерывная ;

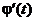3. 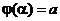и .

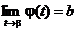Тогда имеет место формула

.

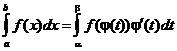Доказательство.

Пусть 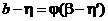. В силу непрерывност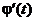и при 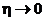также и 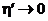. Вспоминая замену переменных в определенных интегралах, имеем:

.

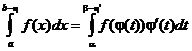После предельного перехода 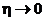, получаем

. <

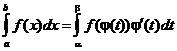Пример.

Рассмотрим интеграл 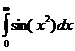, который называется интегралом Френеля. Вопрос о его сходимости не может быть решен на основании изученных нами признаков.

Сделаем замену переменных 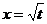. Тогда 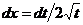и мы имеем:

.

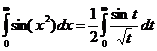Получившийся интеграл сходится по признаку Дирихле.

Интегралы Фруллани

Пусть

1. функция 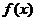определена и непрерывна при ;

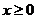2. существует конечный ;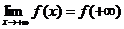

3. .

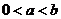Рассмотрим следующий интеграл:

.

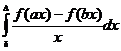Имеем

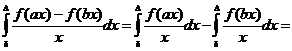
В первом интеграле сделаем замену переменных 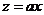, во втором - 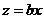: получаем

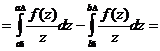
И теперь - самое интересное. Посмотрите на области интегрирования первого и второго интегралов:

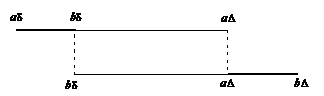
У них есть общая часть - отрезок . Подынтегральные функции одинаковы, интегралы вычитаются - следовательно, интегралы по этой области сокращаются. Остается

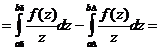
А теперь срабатывает первая теорема о среднем

,

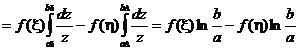где , .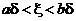

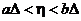А теперь сделаем предельный переход при 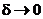, 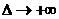. Тогда 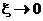, 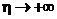и мы получаем

.

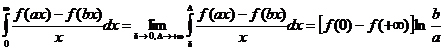Интеграл 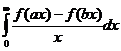называется интегралом Фруллани. Полученная формула позволяет легко вычислять их.

Интегральные неравенства

Неравенство Гёльдера.

Выведем одно из важнейших неравенств математического анализа - неравенство Гёльдера.

Пусть p и q - вещественные числа, такие, что

1. , :

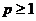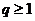2. (самое главное) .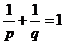

Прежде, чем выводить само неравенство, выведем некоторые промежуточные формулы, чтобы потом не отвлекаться. Имеем

; ; ; .

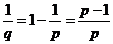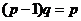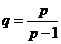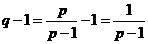А теперь - вперед!

Неравенство Минковского

Неравенство Иенсена

Это неравенство мы выведем не очень строго.

Пусть

1. 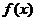есть выпуклая на 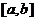функция:

2. 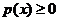и ;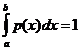

3. 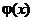непрерывная функция.

Вспомним теперь неравенство Иенсена

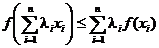
и сделаем в нем следующие замены:

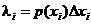, а 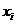заменим на 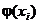. Тогда неравенство Иенсена примет вид

.

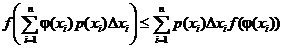Сделаем теперь в этом неравенстве предельный переход 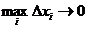. Тогда суммы перейдут в интегралы, и мы получим неравенство

.

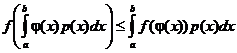Это неравенство и называется неравенством Иенсена в интегральной форме.

Глава 8. Несобственные интегралы

В предыдущей главе при построении теории определенного интеграла явно или неявно предполагались следующие ограничения:

1. отрезок 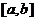имеет конечную длину;

2. подынтегральная функция 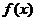ограничена.

Определенные интегралы, построенные при этих ограничениях, называются «интегралами в собственном смысле», или, короче, «собственными интегралами».

Сейчас мы будем отказываться от этих ограничений, и построенные интегралы называются «интегралами в несобственном смысле», или просто «несобственными интегралами».