Несобственные интегралы. Примеры решений

К изучению несобственных интегралов лучше приступать в последнюю очередь в ходе изучения интегрального исчисления функции одной переменной. Читатель данного урока должен быть хорошо подкован в неопределенных интегралах, определенных интегралах, уметь находить площадь плоской фигуры с помощью определенного интеграла. Кроме того, потребуются знания простейших пределови графиков элементарных функций. По логике изложения материала эта статья является продолжением уроков определенный интеграл, вычисление площади фигуры. Тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки.

Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, к тому же у несобственного интеграла есть очень хороший геометрический смысл.

Что значит вычислить несобственный интеграл? Вычислить несобственный интеграл – это значит найти ЧИСЛО, точнее, предел последовательности, или доказать, что он расходится, то есть получить в итоге бесконечность вместо числа.

Несобственные интегралы бывают двух видов: первого и второго рода.

Несобственный интеграл с бесконечным пределом (ами) интегрирования

Иногда такой несобственный интеграл еще называют

несобственным интегралом первого рода.

В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так:

.

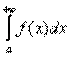В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный:

.

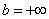Встречаются интегралы и с бесконечным нижним пределом

,

или с двумя бесконечными пределами:

.

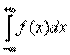Мы начнём с рассмотрения самого популярного случая

.

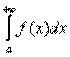Техника работы с другими разновидностями – аналогична.

Всегда ли существует несобственный интеграл

?

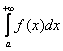Нет, не всегда.

Подынтегральная функцияf(x)должна быть непрерывной на интервале [a; +∞), или иметь устранимые разрывы, и быстро сходиться на бесконечности.

Строго говоря, если есть разрывы функции, то в ряде случаев можно разбить интервал на несколько частей и вычислить несколько несобственных интегралов.

Изобразим на чертеже график подынтегральной функции f(x). Типовой график и криволинейная трапеция для данного случая выглядит так:

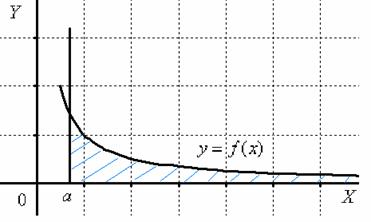
Здесь подынтегральная функция f(x) непрерывна на интервале [a; +∞). Обратите внимание, что криволинейная трапеция у нас – бесконечная (не ограниченная справа) фигура. И, чтобы площадь криволинейной трапеции существовала, она должна, при стремлении x к +∞, стремиться к конечному числу (быть конечным числом).