Несобственные кратные интегралы
Если функция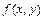 
непрерывна в неограниченной области 
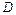, то по определению полагают 
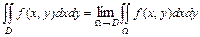, где 
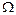- ограниченная замкнутая область, которая целиком лежит в области 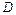и стремится к 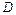произвольным образом. Если предел в правой части существует и не зависит от выбора области 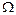, то соответствующий несобственный интеграл по бесконечной области называется сходящимся, в противном случае расходящимся. Предел в правой части не зависит от выбора 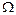, если 
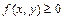в области .
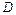Если функция 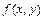непрерывна в ограниченной замкнутой области 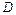всюду, за исключением точки 
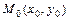, то по определению полагают 
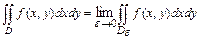, где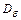 
- область, получаемая из 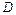путём удаления малой области диаметра 
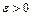, содержащей точку 
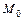. Если предел в правой части существует и не зависит от вида удаляемых из 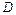малых областей, то соответствующий несобственный интеграл от разрывной функции называется сходящимся, в противном случае расходящимся. Предел в правой части не зависит от вида удаляемых из 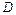малых областей, если 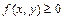в области 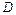и в этом случае, в качестве таких областей можно брать круги радиуса 
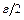с центром в точке .
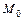Аналогично определяется несобственный интеграл, если функция 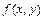в ограниченной замкнутой области 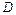имеет линию разрыва 
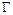. В этом случае 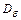- область, получаемая из 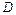путём удаления полосы малой ширины 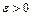, содержащей линию разрыва .
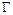В задачах 10.143-10.154вычислить несобственные интегралы по бесконечной области или установить их расходимость:
10.143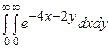 
. 10.144 
.
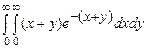10.145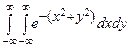 
. 10.146 
.
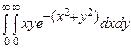10.147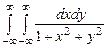 
. 10.148 
.
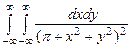10.149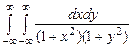 
. 10.150 
.
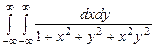10.151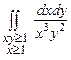 
. 10.152 
.
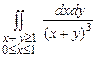10.153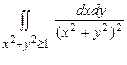 
. 10.154 
.
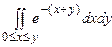В задачах 10.155-10.160 вычислить несобственные интегралы от разрывных функций или установить их расходимость:
10.155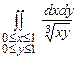 
. 10.156 
.
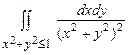10.157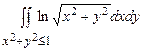 
. 10.158 
.
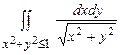10.159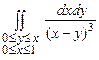 
. 10.160 
.
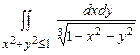ГЛАВА 11. КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ
ИНТЕГРАЛЫ. ТЕОРИЯ ПОЛЯ.
Криволинейный интеграл первого рода и его приложения.
Если 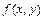- функция, определённая и непрерывная в точках гладкой плоской кривой 
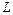, заданной уравнением 
( 
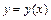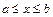) и 
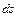- дифференциал дуги, то криволинейный интеграл 1-го рода вычисляется по формуле 
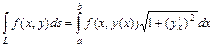. В случае параметрического задания кривой : 
, 
( 
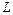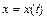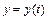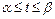) имеет место формула 
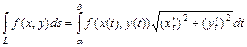. Если плоская кривая 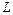задана уравнением 
( 
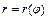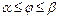) в полярных координатах, то 
.
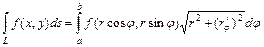Если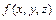 
- функция, определённая и непрерывная в точках гладкой пространственной кривой : , , 
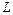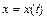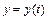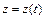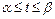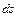( ) и - дифференциал дуги, то криволинейный интеграл 1-го рода вычисляется по формуле
.
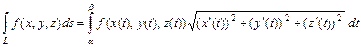Особенность криволинейного интеграла 1-го рода состоит в том, что он не зависит от направления пути интегрирования.
Длина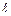 
дуги кривой 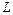вычисляется по формуле 
. Масса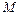 
дуги кривой 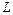с плотностью 
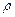вычисляется по формуле 
.
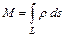Если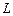 
- дуга плоской кривой с плотностью 
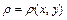, то её статические моменты 
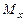и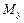 
, моменты инерци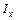и 
и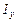 
относительно осе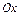й 
и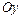 
, координаты 
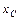и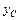 
центра масс 
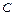вычисляются
по формулам: