Наименьшее и наибольшее значения функции на сегменте

Пусть функция 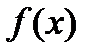определена и непрерывна на 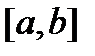, дифференцирована в 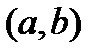, за исключением конечного количества точек. По первой и второй теоремам Вейерштрасса она ограничена и достигает на этом сегменте своих точных верхней и нижней границ, которые являются ее наибольшим и наименьшим значениями на этом сегменте. Надо эти значения найти.

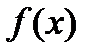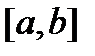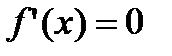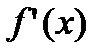Допустим, что не имеет на точек, где , или не существует. Это означает, что 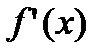сохраняет свой знак везде на 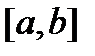, а функция 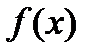- строго монотонна на 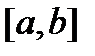. Тогда наименьшее и наибольшее значения она будет принимать на концах сегмента .

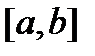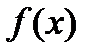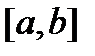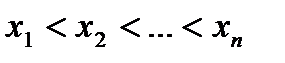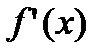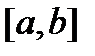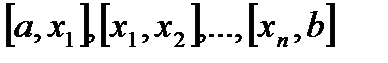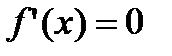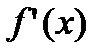Если на сегменте имеет конечное число точек , где не существует или равняется нулю, то эти точки разбивают сегмент на частичные сегменты: , в каждом из которых уже нет таких точек, где или не существует, а потому 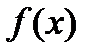- строго монотонна на каждом из 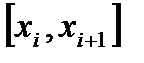, а потому наименьшее и наибольшее значения она будет принимать на концах .

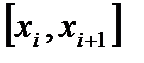Таким образом, для того, чтобы найти наименьшее и наибольшее значения непрерывной на сегменте 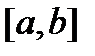функции надо:

1. Найти производную функции на ;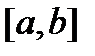

2. Найти все стационарные точки функции, и точки, в которых 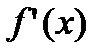не существует, которые принадлежат 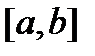. Обозначим эти точки ;

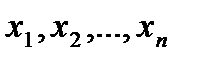3. Вычислить значения ;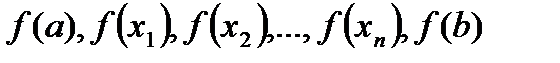

4. Сравнить все значения, полученные на предыдущем шаге, и выбрать из них наименьшее и наибольшее.

Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).

Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.

Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.

Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2^у-х+у=0).

Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.

Производная неявной функции выражается через аргумент х и функцию у.

Рассмотрим одно из геометрических приложений частных производных функции двух переменных. Пусть функция 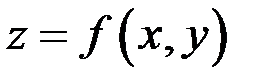дифференцируема в точке 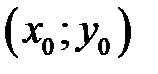некоторой области 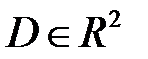. Рассечем поверхность 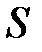, изображающую функцию 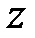, плоскостями 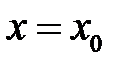и .

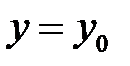Плоскость 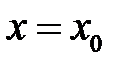пересекает поверхность 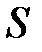по некоторой линии 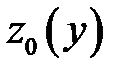, уравнение которой получается подстановкой в выражение исходной функции 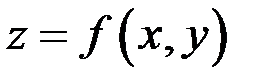вместо 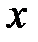числа 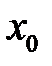. Точка 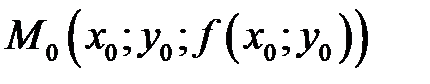принадлежит кривой 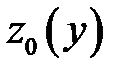. В силу дифференцируемости функции 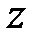в точке 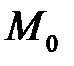функция 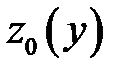также является дифференцируемой в точке 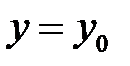. Следовательно, в этой точке в плоскость 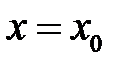к кривой 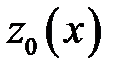касательная .

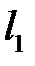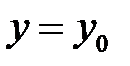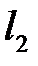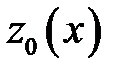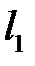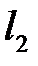Проводя аналогичные рассуждения, для сечения построим касательную к кривой . Прямые и определяют плоскость 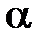, которая называется касательной плоскостью к поверхности 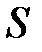в точке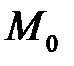

Составим её уравнение. Так как плоскость 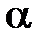проходит через точку 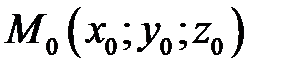, то её уравнение может быть записано в виде

,

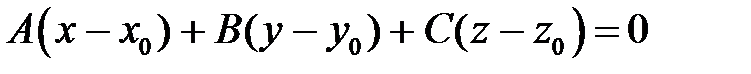которое можно переписать так:

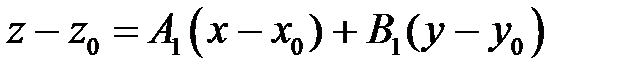(1)

( разделив уравнение на 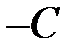и обозначив ).

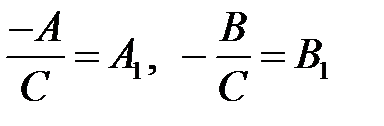Найдем 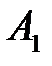и .

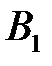Уравнения касательных 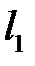и 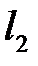имеют вид

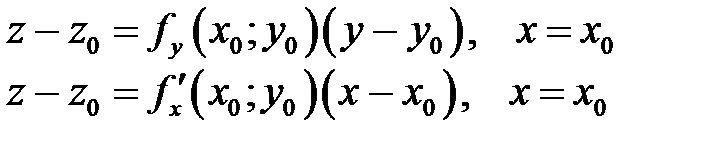
соответственно.

Касательная 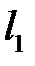лежит в плоскости 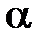, следовательно, координаты всех точек 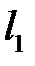удовлетворяют уравнению (1). Этот факт можно записать в виде системы

.

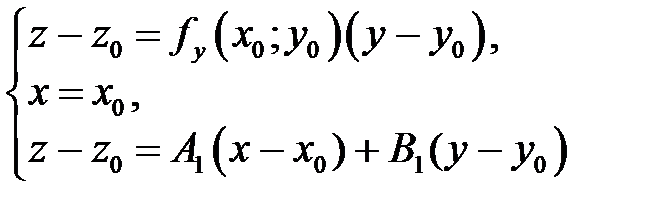Разрешая эту систему относительно 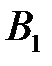, получим, что .

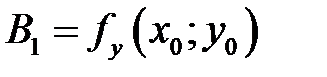Проводя аналогичные рассуждения для касательной 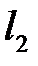, легко установить, что .

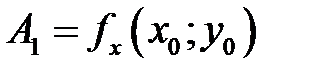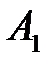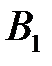Подставив значения и в уравнение (1), получаем искомое уравнение касательной плоскости:

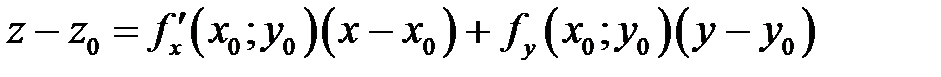(2)

Прямая, проходящая через точку и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется её нормалью.

Используя условие перпендикулярности прямой и плоскости легко получить каноническое уравнение нормали:

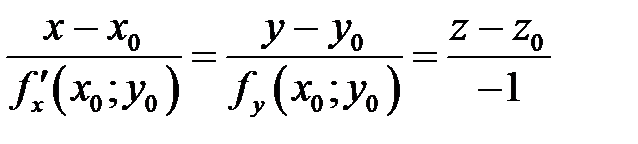(3)

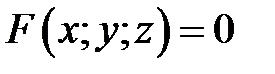Если поверхность задана уравнением , то уравнения (2) и (3), с учетом того, что частные производные могут быть найдены как производные неявной функции:

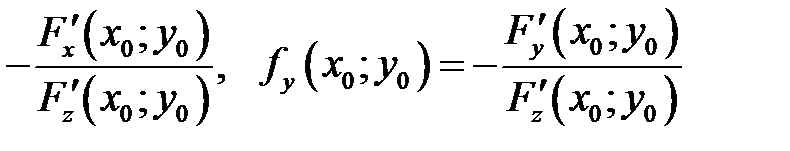
Теорема существования.Если:

1) функция 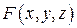обращается в нуль в некоторой точке ;

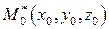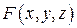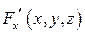2) и определены и непрерывны в окрестности точки ;

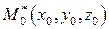3) ,

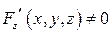то в некоторой достаточно малой окрестности точки 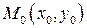существует единственная однозначная непрерывная функция

,

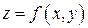удовлетворяющая уравнению

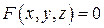
и такая, что .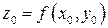

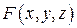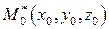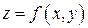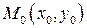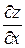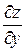Частные производные функций, заданных неявно. Если выполнены все условия приведенной выше теоремы и, кроме того, функция дифференцируема в окрестности точки , то функция дифференцируема в окрестности точки и ее производные и могут быть найдены из уравнений

.

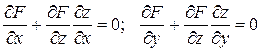Если функция 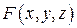дифференцируема достаточное число раз, то последовательным дифференцированием этих уравнений вычисляются производные высших порядков от функции .

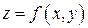Дифференцирование неявных функций, заданных системой уравнений. Пусть функции 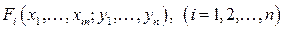удовлетворяют следующим условиям:

1) обращаются в нуль в точке ;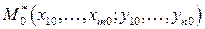

2) дифференцируемы в окрестности точки ;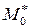

3) функциональный определитель (якобиан) 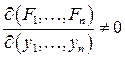в точке .

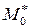Тогда система уравнений

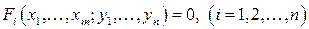
однозначно определяет в некоторой окрестности точки 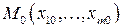систему дифференцируемых функций

, ,

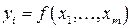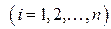удовлетворяющих системе уравнений 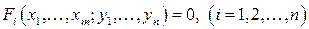и начальным условиям

, .

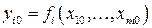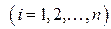Дифференциалы этих неявных функций могут быть найдены из системы

.

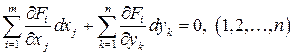Вектор 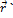( 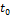) является вектором касательной кривой 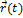в точке 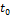. Обозначим точку кривой 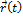, соответствующую значению параметра 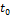, через P, т.е.P=P 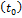. Плоскость, проходящая через точкуP 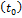кривой и перпендикулярная вектору 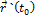, называется нормальной плоскостью кривой в точке 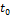.По вектору 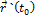= 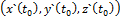и точке P 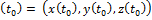запишем уравнения касательной прямой и нормальной плоскости кривой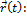

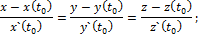
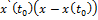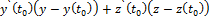+ =0.