Связь дискретных и непрерывных процентных ставок. Для непрерывных процентов не существует различий между процентной и учетной ставками, поскольку сила роста - универсальный показатель

Для непрерывных процентов не существует различий между процентной и учетной ставками, поскольку сила роста - универсальный показатель. Однако наряду с постоянной силой роста может использоваться переменная процентная ставка, величина которой меняется по заданному закону (математической функции).

Непрерывное начисление процентов используется при анализе сложных финансовых задач, например, обоснование и выбор инвестиционных решений. Оценивая работу финансового учреждения, где платежи за период поступают многократно, целесообразно предполагать, что наращенная сумма непрерывно меняется во времени и применять непрерывное начисление процентов.

Все ситуации, которые мы до сих пор рассматривали, относились к дискретным процентам, поскольку их начисление осуществляется за фиксированные промежутки времени (год, квартал, месяц, день, час). Но на практике нередко встречаются случаи, когда проценты начисляются непрерывно, за сколь угодно малый промежуток времени. Если бы проценты начислялись ежедневно, то годовой коэффициент (множитель) наращения выглядел так:

k_н = (1 + j / m)^m = (1 + j / 365)³⁶⁵

Но поскольку проценты начисляются непрерывно, то m стремится к бесконечности, а коэффициент (множитель) наращения стремится к e ^j:

где e ? 2,718281, называется числом Эйлера и является одной из важнейших постоянных математического анализа.

Отсюда можно записать формулу наращенной суммы для n лет:

FV = PV * e ^{j * n} = P * e ^{д * n}

Ставку непрерывных процентов называют силой роста (force of interest) и обозначают символом д, в отличие от ставки дискретных процентов ( j ).

Пример. Кредит в размере на 100 тыс. долларов получен сроком на 3 года под 8% годовых. Определить сумму подлежащего возврату в конце срока кредита, если проценты будут начисляться:

а) один раз в год;

б) ежедневно;

в) непрерывно.

Решение:

Используем формулы дискретных и непрерывных процентов:

начисление один раз в год

FV = 100'000 * (1 + 0,08)³ = 125'971,2 долларов;

ежедневное начисление процентов

FV = 100'000 * (1 + 0,08 / 365)^{365 * 3} = 127'121,6 долларов

непрерывное начисление процентов

FV = 100'000 * e^{0,08 * 3} = 127'124,9 долларов.

14. Срок ссуды. Необходимые для расчета продолжительности ссуды в годах и днях формулы

срок в годах

;

срок в днях (напомним, что n = t/K,где K — временная база)

.

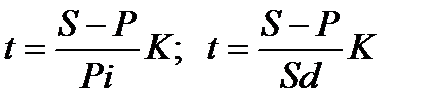Величина процентной ставки. Необходимость в расчете процентной ставки возникает при определении финансовой эффективности операции и при сравнении контрактов по их доходности в случаях, когда процентные ставки в явном виде не указаны. Решив выражения (1.1) и (1.8) относительно i или d,получим

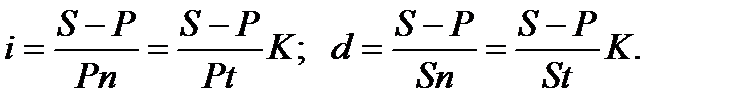
Срок платежа. Приведем формулы расчета п для различных условий наращения процентов и дисконтирования. При наращении по сложной годовой ставке i и по номинальной ставке j соответственно получим:

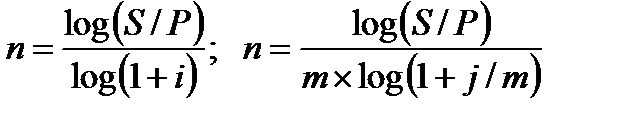. (2.23) (2.24)

При дисконтировании по сложной годовой учетной ставке d и по номинальной учетной ставке f

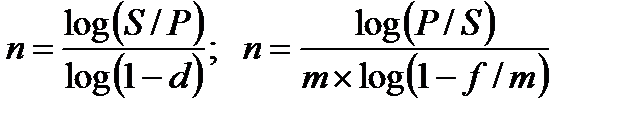. (2.25) (2.26)

При наращении по постоянной силе роста δ и по изменяющейся с постоянным темпом силе роста

.

Величина процентной ставки. Приведем формулы для расчета ставок i, j, d, f, δ для различных условий наращения процентов и дисконтирования. Они получены при решении уравнений, определяющих S и Р, относительно искомых ставок.

При наращении по сложной годовой ставке процентов и по номинальной ставке процента т раз в году находим

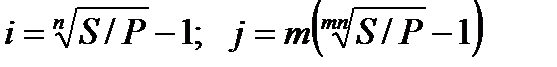. (2.29) (2.30)

При дисконтировании по сложной учетной ставке и по номинальной учетной ставке

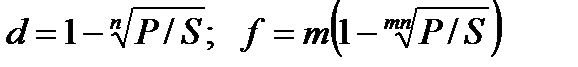. (2.31) (2.32)

При наращении по постоянной силе роста

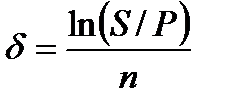. (2.33)

При наращении по изменяющейся с постоянным темпом силе роста

.

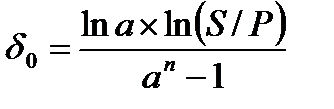15.Начисление простых процентов в условиях инфляции. Вернемся к проблеме обесценения денег при их наращении. В общем случае теперь можно записать:

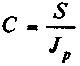(2.42)

Если наращение производится по простой ставке, имеем:

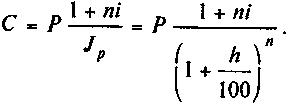(2.43)

Как видим, увеличение наращенной суммы с учетом сохранения покупательной способности денег имеет место только тогда, когда 1 + ni > J_p.

Пример. Допустим, на сумму 1,5 млн. руб. в течение трех месяцев начисляются простые проценты по ставке 50% годовых (K = 360). Наращенная сумма равна 1,6875 млн. руб. Если ежемесячная инфляция характеризуется темпами, приведенными в примере 2.22,б, то с учетом обесценения наращенная с0умма составит всего 1,6875/1,77 = 0,9534 млн. руб.

16.Начисление сложных процентов в условиях инфляции. Обратимся теперь к наращению по сложным процентам. Подставив в формулу (2.42) значения S и J_p, находим

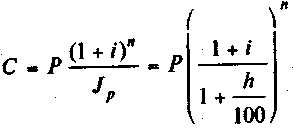(2.44)

Величины, на которые умножается Р в формулах (2.43) и (2.44), представляют собой множители наращения с учетом инфляции. Пример. Найдем реальную ставку сложных процентов для условий: годовая инфляция 120%, брутто-ставка 150%:

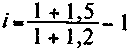= 0,1364, или 13,68% (по упрощенной формуле 30%).

Другой метод компенсации инфляции сводится к индексации первоначальной суммы платежа Р. В этом случае эта сумма периодически корректируется с помощью заранее оговоренного индекса. Такой метод принят в Великобритании. По определению

C = PJ_p(1 + i)ⁿ.

17.Расчёт реальной процентоной ставки в условиях инфляции. Перейдем теперь к решению обратной задачи — к измерению реальной ставки процента, т.е. доходности с учетом инфляции — определению i по заданному значению брутто-ставки. Если r — объявленная норма доходности (брутто-ставка), то искомый показатель доходности в виде годовой процентной ставки i можно определить при начислении простых процентов на основе (2.43) как

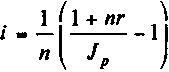. (2.48)

Реальная доходность, как видим, здесь зависит от срока наращения процентов. Напомним, что фигурирующий в этой формуле индекс цен охватывает весь период начисления процентов.

Аналогичный по содержанию показатель, но при наращении по сложным процентам найдем на основе формулы (2.44):

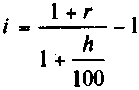. (2.49)

Если брутто-ставка определяется по упрощенной формуле (2.47), то

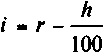. (2.50)

Показатель доходности здесь не зависит от срока начисления процентов. Положительной ставка i может быть только при условии

при начислении простых процентов и r > h при начислении сложных процентов.