Методические указания к задаче 11

В задаче 11 необходимо по параметрам табл. 1 и 2 построить исходные данные; задать откосы насыпей и выемок; построить линии пересечения откосов с топографической поверхностью; построить сечение сооружения плоскостью, заданной в варианте задания (рис 32 — 36).

Выполнению задачи 11 должно предшествовать изучение темы “Проекции с числовыми остатками”.

Сущность метода. проекции точки

Метод проекций с числовыми отметками является частным случаем ортогональных проекций. Он применяется при изображении таких инженерных сооружений, как полотно железных и шоссейных дорог, плотин, дамб, аэродромов - т.е. в тех случаях, когда высота объекта существенно меньше его размеров на плане.

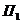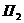Сущность метода заключается в. том, что вместо двух проекций предмета (на плоскостях и ) на ортогональном чертеже изображают одну, чаще всего горизонтальную проекцию и рядом с проекцией каждой точки предмета указывают в виде индекса ее отметку (число), определяющую расстояние обычно в метрах от точки до плоскости проекций 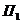(координата Z). Плоскость 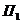называют плоскостью нулевого уровня и обозначают как 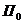(рис. 1).

При изображении топографической поверхности за такую плоскость принимают поверхность уровня моря. Точки, расположенные ниже плоскости нулевого уровня, имеют отрицательные отметки и на чертеже проставляются со знаком минус. Точки, принадлежащие плоскости 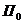имеют нулевую отметку (рис.1).

рис. 1 рис. 2

Чертежи, выполненные в проекциях с числовыми отметками, принято называть планами, на которых показывают линейный масштаб, необходимый для решения метрических задач (рис.2).

План должен быть определенным образом ориентирован относительно сторон света. На нем а виде стрелки с пометками "С", "Ю" (север, юг) показывают положение меридиана. Если боковая линия рамки чертежа совпадает с положением меридиана, его можно специально не обозначать.

ПРЯМАЯ ЛИНИЯ

Для изображения в проекциях с числовыми отметками отрезка прямой АВ (рис. 3) показывают проекции двух её точек А и В.

Длину проекции отрезка 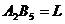называют заложением прямой. Разность расстояний до плоскости 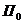концов отрезка 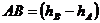называют превышением прямой. Отношение превышения прямой к ее заложению называют уклоном прямой: 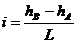. Численно уклон равен 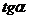, где 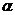- угол наклона прямой к плоскости 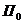. Уклоны выражают в виде простого отношения - 1:1, 1:2 и т.д., в виде процентов - 10%, 20% и т. д.

рис. 3

Длина, заложения отрезка прямой, у которого превышение равно единице, называется интервалом прямой. Чтобы получить интервал, нужно заложение прямой разделить на ее превышени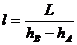е, , где 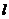- интервал прямой. Между уклоном прямой и ее интервалом - обратная зависимость, т.е. 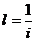и .

И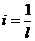нтервал прямой можно построить графически. Для этого нужно отрезок прямой повернуть вокруг его проекции и совместить его с плоскостью 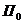(см.рис.3). Из концов проекций отрезка проводят перпендикуляры, на которых в масштабе чертежа откладывают расстояния от точек А и В до плоскости 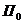или превышение прямой. Затем на прямой АВ находят точки с целыми отметками, в данном случае точки 3 и 4, и проецируют их на плоскость 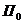. Отрезки на проекции прямой 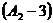, , 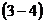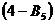равны интервалу. Угол 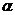- угол наклона прямой к плоскости 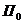. АВ - действительная длина отрезка АВ.

ПЛОСКОСТЬ

Плоскость в проекциях с числовыми отметками часто задают ее масштабом падения (уклона) – градуированной проекцией линии наибольшего ската плоскости. Масштаб падения на чертеже изображают двумя параллельными прямыми (толстой и тонкой) и обозначают той же буквой, что и плоскость, но с индексом i, например - 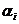: (рис. 4). Масштаб падения перпендикулярен проекциям горизонталей плоскости. Расстояние 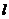между проекциями соседних горизонталей, разность отметок которых равна единице, называется интервалом плоскости. Он так же, как и для прямой - величина обратная уклону плоскости, т.е. .

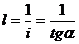рис. 4

ПРОЕКЦИИ ТЕЛ И ПОВЕРХНОСТЕЙ

Поверхности в проекциях с числовыми отметками изображаются горизонталями, являющимися результатом пересечения заданной поверхности рядом плоскостей параллельных плоскости 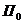и отстоящих друг от друга на расстояние равное единице длины.

На рис.5 показано изображение в проекциях с числовыми отметками прямого кругового конуса. Проекции его горизонталей - концентрические окружности, расстояния между которыми равны интервалу 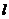образующей конуса.

рис. 5

Топографическая поверхность (естественная поверхность земли) имеет неправильную форму, поэтому ее горизонтали - кривые линии неправильной формы. На рис.6 схематично изображен холм, горизонталями которого будут линии пересечения его поверхности с горизонтальными плоскостями 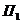, 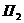и т.д. В практике горизонтали топографической поверхности проводят через проекции точек, имеющих одинаковые отметки, определенные в процессе геодезической съемки местности. В задаче 11 горизонтали топографической поверхности заданы.

рис. 6

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Рассмотрим решения в проекциях с числовыми отметками некоторых примеров, встречающихся при выполнении задачи 11 контрольной работы №2.

На рис.7 показано построение линии пересечения плоскосте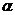й и 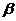. Такая задача может встретиться при определении линии пересечения плоских откосов насыпей или выемок. Искомая проекция линии пересечения 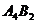плоскосте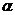й и 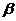проходит через точки пересечения двух пар "одноименных" (с одинаковыми отметками) горизонталей заданных плоскостей.

рис. 7 рис. 8

Линия пересечения плоскости с поверхностью конуса будет проходить через точки пересечения одноименных горизонталей этих поверхностей. Решение этой задачи также встречается в практике строительного проектирования и в контрольной работе №2, так как откосы насыпей или выемок могут иметь коническую форму. На рис.8 показан пример решения такой задачи. Проекция линии пересечения конической поверхности с плоскостью 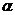проходит через точки .

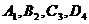Линия пересечения топографической поверхности с горизонтально - проецирующей плоскостью 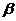(рис.9) носит название профиля топографической поверхности. Построение этой линии - распространенная в строительном проектировании задача. Для ее решения рекомендуется следующий практический прием. К проекции плоскости 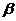, ее горизонтальному следу 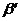прикладывается полоска бумаги, куда переносятся точки пересечения плоскости с горизонталями топографической поверхности 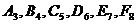. Полученные точки переносят на горизонтальную линию - основание профиля, отметку которой задают условно. В данном случае отметка основания 3,00. Затем в масштабе чертежа из отмеченных точек откладывают по перпендикуляру вверх превышения отмеченных точек (разность отметки точки и принятой отметки основания профиля). Искомая линия профиля (сечения плоскости с топографической поверхностью) будет проходить через точки .

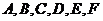рис. 9 рис. 10

На рис.10 заданы топографическая поверхность и горизонтальный участок полотна дороги, отметка которого 12,00 м. Дорога будет расположена на насыпи, так как отметки горизонталей местности (топографической поверхности) меньше отметки полотна дороги. Требуется определить границы насыпи дороги. Уклон откосов насыпи задан и равен 1:1,5, поэтому интервал плоскостей откосов насыпи будет равен 1,5 м. Граница насыпи пройдет через точки пересечения одноименных горизонталей откосов насыпи и топографической поверхности. Проводим параллельно бровке дороги горизонтали плоскости южного откоса насыпи и отмечаем точки 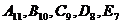, через которые проходит искомая линия. Аналогично строится линия пересечения топографической поверхности с северным откосов насыпи.

На плане берг-штрихами показывают направление ската воды вдоль откосов. Берг-штрихи изображаются сплошной тонкой линией через 2...5 мм (рис.10).

На рис.11 та же задача решена для горизонтального участка дороги, расположенного на круговой кривой. Откосы насыпи в этом случае имеют коническую форму, а горизонтали откосов - концентрические окружности. Граница откоса насыпи будет проходить через точки 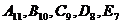, где пересекаются горизонтали конического откоса с одноименными горизонталями топографической поверхности.

рис. 11 рис. 12

Несколько сложнее решается эта задача для случая, когда дорога расположена на наклонном участке (см. рис.12). В этом случае горизонтали плоского откоса не будут параллельны бровке дороги, так как она будет наклонная. Горизонтали откосов насыпи будут касательны к одноименным горизонталям конусов с вершинами, принадлежащими бровке полотна дороги, образующие которых имеют тот же уклон, что и откосы насыпи. Например, на рис.12 вершины конусов расположены в точках 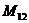. Горизонталь южного откоса насыпи с отметкой 11 проходит через точку с отметкой 11, расположенную на бровке полотна и касательную к горизонтали конуса с отметкой 11. Остальные горизонтали откоса насыпи будут параллельны проведенной горизонтали с отметкой 11. Искомая линия пересечения пройдет через точки пересечения одноименных горизонталей насыпи и топографической поверхности . Также строится и граница северного откоса насыпи. Аналогично решается эта задача и для случая, когда дорога расположена в выемке, разница только в том, что отметки горизонталей по мере удаления от бровки полотна будут не уменьшаться, а возрастать.

ПРИМЕРЫ РЕШЕНИЯ КОНТРОЛЬНЫХ ЗАДАНИЙ 11

Пример решения задачи 11 для студентов специальности ПГС приведен на рис.13, на котором задана топографическая поверхность и расположенная на ней горизонтальная строительная площадка с отметкой 28, а также наклонный въезд на площадку (аппарель). Заданы уклоны насыпи 1:1,5; выемки 1:2 и дороги (аппарели) 1:5.

Часть площадки, расположенная к западу от 28 горизонтали топографической поверхности, будет расположена в выемке, а к востоку от этой горизонтали - на насыпи. Проекции горизонталей плоских откосов площадки будут прямые, параллельные ее бровке и отстоящие друг от друга на 1,5 м в масштабе чертежа для насыпи и на 2 м для выемки. Построение линий пересечения их с топографической поверхностью сводится к решению примера, рассмотренного на рис.10.

рис. 13 рис. 14

Поверхность выемки, примыкающей к криволинейной части площадки, будет конической, а горизонтали откоса этой части выемки будут концентрическими окружностями, расстояния между которыми (интервалы) будут 2 м. Построение линии пересечения конического откоса с топографической поверхностью показано на рис.11.

Аппарель (наклонный въезд на площадку) имеет уклон, горизонтали аппарели будут расположены на расстоянии 5 м друг от друга, а горизонтали откосов насыпи аппарели будут касательны к горизонталям конусов, имеющих вершины на бровке аппарели. Граница откосов насыпи аппарели строится аналогично построениям, приведенным на рис. 12.

Линия пересечения откосов конической и плоской частей выемки пройдет через точки и будет криволинейной (часть параболы). Линия пересечения плоскостей откосов, имеющих одинаковый уклон будет проецироваться по биссектрисе угла между горизонталями плоскости (см., например, линию 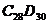). Восточный откос площадки и южный откос аппарели пересекаются по прямой 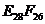. Аналогично строятся и другие участки искомых линий.

При построении линий пересечения откосов с топографической поверхностью часто приходится определять точки, принадлежащие этой линии и расположенные вне пределов рассматриваемых откосов, например, точки 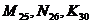на рис. 13 или точки 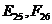на рис. 14. Эти точки вспомогательные, необходимые для построения границы земляных работ на участках непосредственно прилагающих к линиям пересечения откосов.

Профиль местности строят аналогично примеру, рассмотренному на рис.9. На профиле показывают попавшие в секущую плоскость контуры горизонтальной площадки, наклонной дороги и откосов насыпи и выемки.

Пример решения задачи 11 для студентов специальностей С, МТ и ВК показан на рис.14. Здесь задана топографическая поверхность и полотно дороги с горизонтальным криволинейным участком радиуса 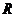и отметкой 28 и наклонным, прямолинейным участком имеющим уклон 1:5.

Определив интервалы наклонного участка дороги - 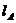, выемки 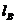и насыпи - 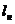, проводят горизонтали аппарели и откосов. Часть дороги, расположенная восточнее горизонтали местности с отметкой 28, будет находиться на насыпи, а западнее этой горизон­тали - в выемке. Затем строят линию пересечения откосов горизонтального и наклонного участков, дороги (см. лини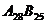и и 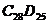на рис.14). Построение линии пересечения откосов насыпей и выемок дороги с топографической поверхностью на прямолинейном участке дороги аналогично рис.12, а на криволинейном - рис. 11.

ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ ЗАДАНИЯ № 11

1. Подготовить формат А-3 (изобразить рамку, основную надпись, размеры которой приведены на рис. 13).

2. Над основной надписью изобразить линейный масштаб Ml:200 (1 м на местности должен соответствовать 5 мм чертежа).

3. Разметить положение горизонталей рельефа местности в соответствии с вариантом и провести их сплошными тонкими линиями. Для этого чертеж задание необходимо увеличить в 4 раза (если методика на формате А4).

4. Студентам специальности ПГС нанести на плане контуры строительной площадки и аппарели, положение которых должно соответствовать исходным данным таблицы 2 подвариантов.

Студентам специальностей С, МТ, ВК изобразить на плане местности контуры горизонтального криволинейного участка доро­ги радиуса R и наклонную аппарель. Центр дуги радиуса R должен располагаться так, чтобы ось дороги пересекала горизонтали топографической поверхности под углом близким к 90°. Поэтому центр дуги радиуса 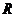может располагаться либо вверху, либо внизу формата в зависимости от значения угла .

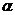Точки нулевых работ целесообразно назначить в пределах горизонтального (криволинейного) участка дороги.

5. Используя линейный масштаб, над основной надписью построить график линейных уклонов насыпи - 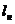= 1:1,5; выемки - 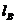= 1:2 и аппарели 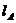= 1:5 и определить интервалы - , , .

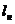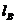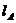6. Определить точки нулевых работ, как точки пересечения горизонтали местности с одноименной отметкой с контуром строительной площадки или дороги. Также определить места расположения насыпей и выемок.

7. Построить масштабы уклонов поверхностей откосов насыпей, выемок, обозначить числовые отметки.

8. Построить горизонтали аппарели, откосов и линии их пересечения.

9. Определить точки пересечения горизонталей топографической поверхности с горизонталями откосов, построить границы откосов насыпей и выемок.

10. По направлению ската воды откоса изобразить берг-штрихи.

11. Обвести линии пересечения откосов насыпей и выемок с топографической поверхностью, сплошной толстой линией.

12. В нижней части формата слева от основной надписи построить профиль строительной площадки или дороги в соответствии с вариантом положения секущей плоскости.

13. Оформить эпюр в соответствии с требованиями, приведенными в разделе «оформление контрольной работы №2».