Ранг матрицы. Способы вычисления ранга матрицы.

Рангом r(A) матрицы A называется наивысший порядок отличного от нуля минора этой матрицы (наибольший из порядков тех определителей, отличных от 0, которые можно составить из рядов матрицы, наибольшее число линейно независимых строк или столбцов таблицы). Не превосходит меньшего из ее размеров.

1 метод нахождения: нахождение наибольшего из порядковых определителей, не равных 0, составленных из рядов данной матрицы

2 метод: приведение матрицы к ступенчатому виду путем элементарных преобразований, ранг будет равен числу не нулевых строк.

Ранг диагональной матрицы порядка n равен числу ее ненулевых элементов

При элементарных преобразованиях матрицы ее ранг не изменяется

Теорема Кронекера-Капелли.

Система Совместна (имеет хотя бы одно решение) тогда и только тогда, когда Ранг матрицы системы равен рангу расширенной матрицы. Система линейных уравнений имеет решение, если ранг матрицы системы равен рангу расширенной матрицы, причем, если он равен и числу неизвестных, то решение – единственное. Если ранг расширенной матрицы больше ранга матрицы системы, то система решения не имеет

Запись и решение системы линейных алгебраических уравнений в матричном виде.

алгебраических уравнений вида 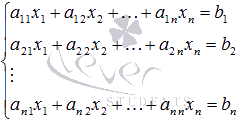, которые в матричной форме записываются как 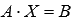, где 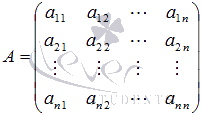- основная матрица системы, 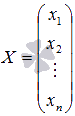- матрица-столбец неизвестных переменных, 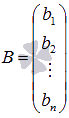- матрица свободных членов.

Решение системы линейных алгебраических уравнений методом Гаусса.

1. Записываем матрицу в расширенном виде:

2. С помощью элементарных преобразований приводим ее к ступенчатому виду

3. Переходим назад к переменным и находим их

Понятие действительной функции действительной переменной. График функции. Основные свойства функций.

Если каждому значению х множества Х ставится в соответствие вполне определенное значение y множества Y, то говорят, что на множестве Х задана функцияy=f(x)

График функции —представление о геометрическом образе функции. Графический способ задания функции состоит в изображении графика функции - множества точек плоскости, абсциссы которых есть значения аргумента х, а ординаты – соответствующие у.

Свойства:

· Четностьf(-x)=f(x), нечетность f(-x)=-f(x), общего вида

· Монотонность (возрастающие, убывающие функции - монотонны)

· Ограниченность (если сущеествует такое м>0 что функция меньше м для любого х)

· Периодичность (f(x+T)=f(x))

Предел числовой последовательности. Признаки существования предела последовательности. Основные свойства сходящихся последовательностей.

Число А называется пределом последовательности {a_n}, если для любого ε> 0 существует такой номер N, что все члены последовательности с большими номерами отличаются от А менее, чем на ε.

Предел функции в бесконечности и в точке.