Ранг матрицы. Вычисление ранга матрицы методом окаймляющих миноров и с помощью элементарных преобразований
Определители 2 и 3-го порядков. Вычисление определителя n-го порядка. Свойства определителей 3-го порядка.
Вычисление определителей второго порядка.
Определитель второго порядка (матрицы размера 2 на 2) вычисляется по правилу:
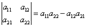Запомнить просто: произведение элементов, стоящих на главной диагонали, минус
произведение элементов, стоящих на побочной.
Вычисление определителей третьего порядка.
Определитель третьего порядка вычисляется по правилу: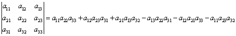 
Запомнить порядок сомножителей, конечно же, очень трудно, если не знать
визуального представления этого правила, которое называется правило треугольников:
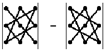
Здесь схематично показано, какие сомножители соседствуют в слагаемых.
Определителем n-го порядка называется число, равное алгебраической сумме всевозможных произведений элементов взятых по одному и только одному из каждой строки и каждого столбца.
Знак каждого слагаемого определяется числом инверсий в перестановках составленных из первых и вторых индексов сомножителей : если оно четное «+», нечетное «-».
Инверсия - когда большее число стоит перед меньшим.
Св-ва определителей:
1. В определителе строки и столбцы равнозначны.
2. Если все Эл-ты в строке или столбце = 0, то определитель =0.
Обратная матрица и ее построение. Теорема существования и единственности обратной матрицы. Матричный метод решения невырожденных систем линейных алгебраических уравнений.
Матрица А наз. невырожденной,если ее определитель не равен 0
Матрица А-1 наз. обратной к матрице А,если АА-1= А-1А=Е, где Е-единичная матрица. Всякая невырожденная матрица имеет единствен. обратную матрицу.
Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем:
Пусть дана система линейных уравнений с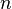 
неизвестными (над произвольным полем): 
Тогда её можно переписать в матричной форме:АХ=В, где А — основная матрица системы, В и Х — столбцы свободных членов и решений системы соответственно:
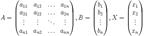
Умножим это матричное уравнение слева на А-1 — матрицу, обратную к матрице А:А-1(АХ)= А-1В Так как А-1А=Е, получаемХ= А-1В. Правая часть этого уравнения даст столбец решений исходной системы
Ранг матрицы. Вычисление ранга матрицы методом окаймляющих миноров и с помощью элементарных преобразований.
Наибольший из порядков миноров данной матрицы отличный от нуля называется рангом матрицы.
rank A = rg A = r
Свойства ранга:
- при транспонировании матрицы ранг не меняется
- если вычеркнуть из матрицы нулевую строку, то ранг не меняется
- ранг матрицы не меняется при элементарных преобразованиях над строками матрицы.
Максимальный порядок r отличных от нуля миноров матрицы A называется ее рангом, а любой минор порядка r, отличный от нуля - базисным минором.
Основные методы вычисления ранга матрицы:
Метод окаймляющих миноров.Пусть в матрице найден минор k-го порядка M, отличный от нуля. Рассмотрим лишь те миноры (k+1)− го порядка, которые содержат в себе (окаймляют) минор M: если все они равны нулю, то ранг матрицы равен k. В противном случае среди окаймляющих миноров найдется ненулевой минор (k+1)−го порядка, и вся процедура повторяется.
Метод элементарных преобразованийоснован на том, что элементарные преобразования матрицы не меняют ее ранга. Используя эти преобразования матрицу можно привести к такому виду, когда все ее элементы кроме a11,a22,...,arr (r≤min(m,n)), равны нулю. Следовательно, ранг матрицы равен r.