Ранг матрицы. Методы вычисления.

Рассмотрим матрицуА размера m × n.

.

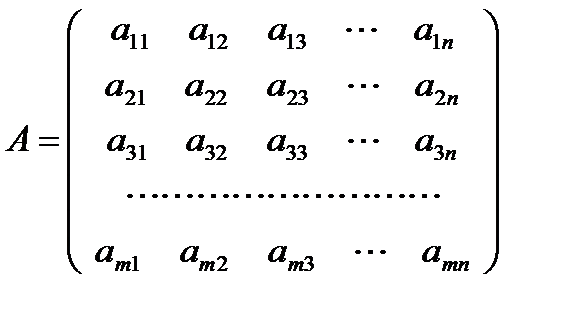Выделим в ней kстрок и k столбцов (k≤ min(m;n)). Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка. Все такие определители называются минорами этой матрицы. В матрицеА пунктиром выделен минор 2-го порядка. (Заметим, что таких миноров можно составить 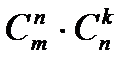штук, где 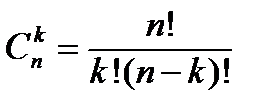– число сочетаний из n элементов по k.)

Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается r, r(A) или rangA.

Очевидно, что , где 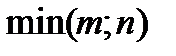– меньшее из чисел m и n.

Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.

Пример 3.4. Найти ранг матрицы:

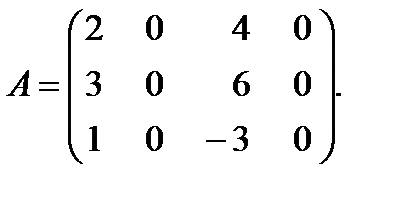
Решение: Все миноры 3-го порядка равны нулю. Есть минор 2-го порядка, отличный от нуля 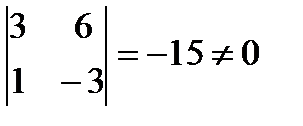. Значит, 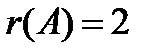. Базисный минор стоит на пересечении 2 и 3 строки с 1 и 3 столбцами.

Отметим свойства ранга матрицы:

1. При транспонировании матрицы ее ранг не меняется.

2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.

3. Ранг матрицы не изменится при элементарных преобразованиях матрицы (см. с. 3).

Ранг канонической матрицы равен числу единиц на главной диагонали. На этом основан один из способов вычисления ранга матрицы.

Пример 3.5. Найти ранг матрицы

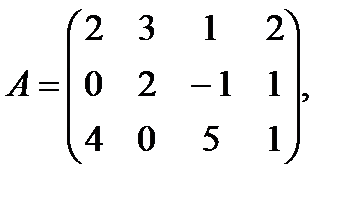
используя результаты примера 1.4.

Решение: В примере 1.4. показано, что

~ ,

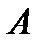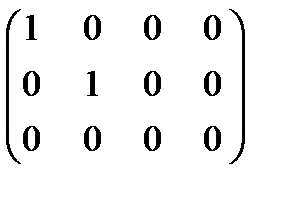то есть

~ .

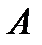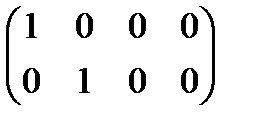Таким образом, ранг матрицы А равен .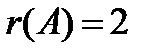

Системы линейных уравнений . Основные понятия.

Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида

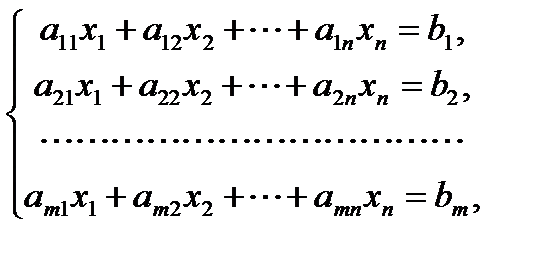
где числа 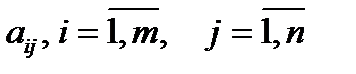называются коэффициентами системы, числа 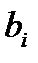– свободными членами. Подлежат нахождению числа .

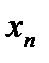Такую систему удобно записывать в компактной матричной форме

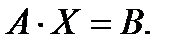ЗдесьА – матрица коэффициентов системы, называемая основной матрицей:

,

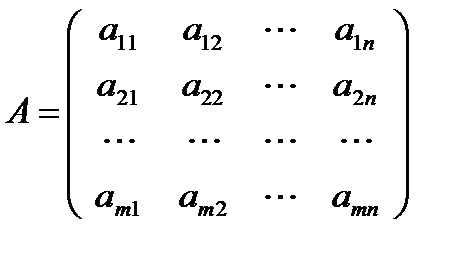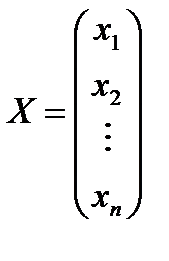– вектор-столбец из неизвестных ,

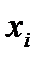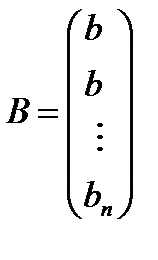– вектор-столбец из свободных членов .

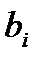Произведение матриц 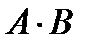определено, так как в матрицеА столбцов столько же, сколько строк в матрице Х (n штук).

Расширенной матрицей системы называется матрица 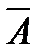системы, дополненная столбцом свободных членов

.

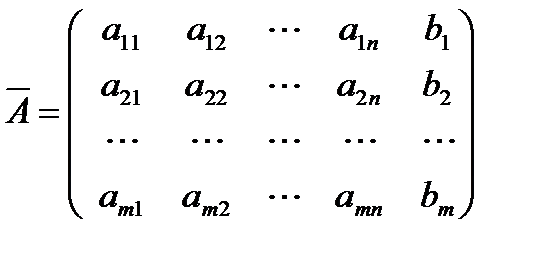Решением системы называется n значений неизвестных 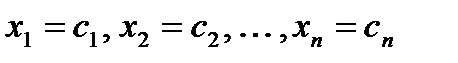, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца .

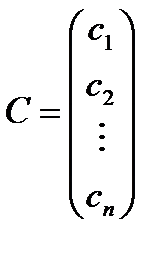Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она ни имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.

Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.

Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются только над строками матрицы.

Система линейных уравнений называется однородной, если все свободные члены равны нулю:

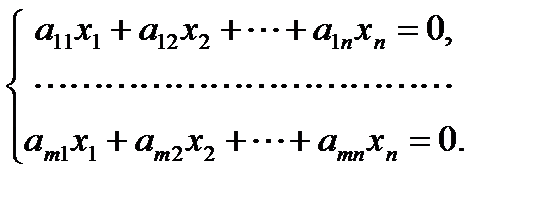
Однородная система всегда совместна, так как 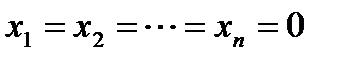является решением системы. Это решение называется нулевым или тривиальным.