III. Понятие минора k-го порядка матрицы. Определение ранга матрицы

Минор к-го порядка матрицы А –определитель, составленный из элементов данной матрицы, расположенных на пересечении каких-либо ее к строк и к столбцов.

Пример: Получим какой-нибудь минор третьего порядка. Рассматриваем три произвольные строки, например, 1-ю, 3-ю и 4-ю, три произвольных столбца, например, 1-й, 2-й и 4-й и с их 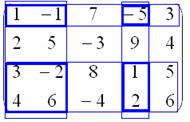пересечения «снимаем» минор 3-го порядка: .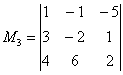

Что касается миноров 4-го порядка, то здесь выбор уже невелик: необходимо задействовать все 4 строки и четыре произвольных столбца, например, все столбцы, за исключением 3-го:

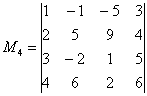
Рангом матрицы А называется наибольший из порядков ее миноров, отличных от «0».

Обозначается: r(A); rang(A)

Свойства ранга:

1. Ранг матрицы А_mxn удовлетворяет неравенству: 0≤r(A)<min(m,n)

2. r(A)=0óA=0

3. A_nxn, r(A)=n ó|A|≠0

4. r(A^T)=r(A)

5. Если вычеркнуть из матрицы нулевые строки (столбцы), то ранг матрицы не изменится.

6. При элементарных преобразованиях ранг матрицы не меняется.

7. Ранг ступенчатой матрицы равен количеству ее ненулевых строк.

Любой ненулевой минор матрицы, порядок которой равен ее рангу, называется базисным или главным минором этой матрицы.

IV. Системы линейных алгебраических уравнений (СЛАУ).

Системой линейных алгебраических уравнений, содержащих m уравнений и n неизвестных, называется система вида:

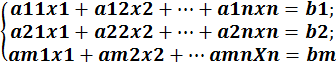
a_ij – коэффициенты;

b_i – свободные члены;

x_j – неизвестные

i =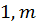

j = 1, n

Система может быть записана в виде: A= 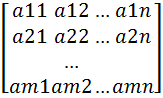Расширенная матрица:

Ȃ=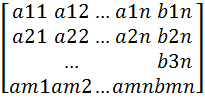

Если СЛАУ имеет хотя бы одно решение, то она называется совместной.

Если система имеет ровно одно решение, то она называется определенной.

Критерии совместности системы. Решение системы методом Гаусса.

Теорема Кронекера-Капелли (критерии совместности системы).

Система СЛАУ является совместной тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы.

r(A)=r(Ȃ)

Если r(A)=r(Ȃ)=n (количество неизвестных, столбцов), то система имеет единственное решение.

Если r(A)=r(Ȃ)<n, то система имеет бесконечное множество решений.

Метод Гаусса.

Решение СЛАУ состоит в том, что с помощью элементарных преобразований система приводится к ступенчатому виду (прямой ход), а затем неизвестное x_ij находят последовательно, начиная с последнего уравнения (обратный ход).

Пример: Если r(A)=2=r(Ȃ)<3, тогда система называется совместной и имеет бесконечное множество решений.

В этом случае внутри матрицы А выбираем какой-либо базисный минор (ненулевой минор, порядок которого равен r(A)). Лучше выбирать треугольный. Те неизвестные, коэффициенты которых вошли в базисный минор, называют главными. Остальные неизвестные называют свободными и переносят в правую часть уравнения.

Обратный ход.

Свободным неизвестным придают произвольные значения (x=c, c?|R).

Главные неизвестные выражают через свободные.

Получаем т.н. общее решение (с, 10-5с, 7-3с)^Т, в котором содержатся все решения данной системы. Подставляя в общее решение конкретные (фиксированные) значения постоянной «с», будем получать конкретные частные решения.

Пример: r(A)=2≠r(Ȃ)=3.

Система несовместна. Ответ: решений нет.

Задание в билете.

Найти координаты точки М, симметричной точке Р(-3,4), относительно прямой 4x-y-1=0.

Задаем уравнение перпендикулярной прямой:

Ax+By+C=0 (перпендикуляр: Bx-Ay+D=0), В=-1; А=4,

-1х-4y+D=0;

Так как точка Р(-3;4) принадлежит прямой, то

-1*(-3)-4*4+D=0

3-16+D=0

D=13. Имеем уравнение перпендикуляра: -1х-4y+13=0;

2) Находим точку пересечения прямых:

4x-y-1=0;

-x-4y+13=0

Решаем: х=1, y=3.

Точка пересечения: N(1,3), точка конца отрезка P(-3;4)

Известны середина и конец отрезка, т.о. через вычисление середины отрезка найдем координаты конца отрезка (симметричную точку)

Точка М (b;c)

1=(-3+b)/2; -3+b=2; b=5.

3=(4+c)/2; 4+c=6; c=2.

M(5;2)