I. «основные сведения о матрицах.
УЧЕБНЫЙ КОМПЛЕКС
ПРЕДМЕТ:
«ВЫСШАЯ МАТЕМАТИКА»
ТЕМА № 1.
«ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ».
Преподаватель Кононова М.П.
I. «ОСНОВНЫЕ СВЕДЕНИЯ О МАТРИЦАХ.
ОПЕРАЦИИ НАД МАТРИЦАМИ»
I. ПОНЯТИЕ МАТРИЦЫ.
Существуют различные способы решения самых разнообразных задач, как математических, так и по специальности. Т.к. математическое моделирование рассматривает и абстрагирует любые объекты, то, например, задача о производстве мучных изделий из имеющегося сырья (данные расположены в таблице ниже)
| Продукт | Блинчики | Оладьи | Вареники | Масса имеющегося сырья |
| Мука | 0,416 кг | 0,481 кг | 0,695 кг | 5 кг |
| Яйца | 0,83 кг | 0,23 кг | 0,53 кг | 0,5 кг |
| Соль | 0,008 кг | 0,009 кг | 0, 012 кг | 0,1 кг |
может быть решена с помощью системы трех уравнений с тремя переменными:
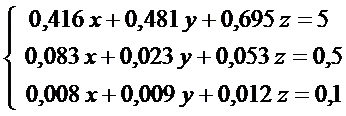
Решить такую систему школьными методами довольно трудоемко, а если получится система с большим количеством уравнений и входящих в них переменных, то и невозможно.
Однако, существуют другие методы решения таких систем, и в этих методах огромную, решающую роль играют коэффициенты при переменных и свободные члены уравнений системы.
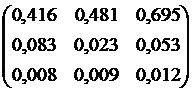 Для этого делают следующую запись:
Для этого делают следующую запись:
Такую запись (она имеет вид таблицы) называют матрицей – матрица позволяет определить другие понятия и решение многих систем различными методами
Понятие матрицы и раздел математики, ее изучающий, имеют чрезвычайно важное значение для экономистов – значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой и компактной матричной форме.
Матрицы широко используются в планировании производства и транспортных перевозок. Они позволяют разрабатывать различные варианты плана, облегчают исследования зависимости между разными экономическими показателями.
Матрицей размера 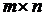 называется прямоугольная таблица чисел, содержащая
называется прямоугольная таблица чисел, содержащая 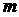 строк и
строк и 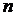 столбцов. Числа, составляющие матрицу, называются элементами матрицы.
столбцов. Числа, составляющие матрицу, называются элементами матрицы.
Рассмотрим еще один пример перехода от таблицы к матрице, с помощью которого разберемся в сути записи матрицы, ее обозначении, нахождении ее размера.

Получаем следующую запись:
 ,
,
где есть прочерки, которые в математике заменяет ноль.
Матрицы обозначаются заглавными прописными буквами латинского алфавита 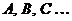 , а размер записывается под обозначением матрицы, причем, согласно определения матрицы, на первом месте записывается количество строк, а на втором – количество столбцов.
, а размер записывается под обозначением матрицы, причем, согласно определения матрицы, на первом месте записывается количество строк, а на втором – количество столбцов.
Таким образом, получаем:
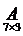 =
=  .
.
Для обозначения элементов матрицы в общем виде используются строчные латинские буквы с двойной индексацией:
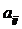 , где
, где 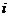 - номер строки,
- номер строки, 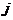 - номер столбца.
- номер столбца.
Пример записи матрицы в общем виде:
 ,
,
или в сокращенной форме: 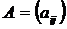 , где
, где 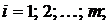
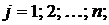
Рассмотрим еще примеры таблиц и матриц:
I.Таблица распределения ресурсов по отделениям отраслям экономки (усл. ед.)
| Ресурсы | Отрасли экономики | |
| промышленность | сельское хозяйство | |
| электроэнергия | 5,4 | 4,2 |
| трудовые ресурсы | 2,7 | 2,1 |
| водные ресурсы | 4,8 | 5,1 |
может быть записана в компактной форме в виде матрицы распределения ресурсов по отраслям:
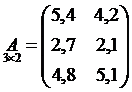
В этой записи матричный элемент 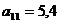 показывает, сколько электроэнергии потребляет промышленность, а элемент
показывает, сколько электроэнергии потребляет промышленность, а элемент 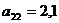 - сколько трудовых ресурсов потребляет сельское хозяйство.
- сколько трудовых ресурсов потребляет сельское хозяйство.
II.Малое предприятие вырабатывает 4 вида продукции A, B, C, D, используя на каждую из них разное количество двух материалов и работы (количества рабочего времени). Конкретная информация указана в таблице.
| Изделия | A | B | C | D |
| Единица материала X | ||||
| Единица материала Y | ||||
| Количество рабочего времени |
В этой ситуации есть 12 действительных чисел, которые можно упорядочить и записать в виде матрицы:
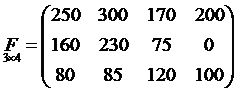
Каждый ряд и каждый столбец этой матрицы имеет определенный смысл. Например, элементы 2го ряда указывают количество материала Y, затраченного на производство продукции A, B, C, D, а элементы 2го столбца матрицы указывают количество затраченных материалов X, Y и рабочего времени на производство продукции B.
II. Виды матриц
1.Две матрицы  и
и 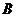 одного размера называются равными, если они совпадают поэлементно, т.е.
одного размера называются равными, если они совпадают поэлементно, т.е. 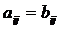 для любых
для любых 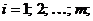
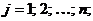 .
.
2. 3. Матрица, состоящая из одной строки, называется матрицей– строкой, а из одного столбца – матрицей -столбцом:
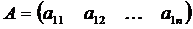 - матрица-строка;
- матрица-строка; 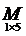 =
= 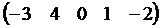 .
.
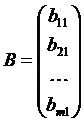 - матрица-столбец,
- матрица-столбец, 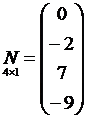 .
.
o Матрица называется квадратной 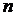 -го порядка, если число ее строк равно числу столбцов и равно
-го порядка, если число ее строк равно числу столбцов и равно 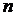 .
.
Пример:
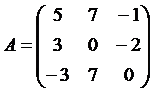 - квадратная матрица 3го порядка
- квадратная матрица 3го порядка
Элементы матрицы 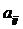 , у которых номер столбца равен номеру строки
, у которых номер столбца равен номеру строки 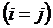 , называются диагональными и образуют главную диагональ матрицы.
, называются диагональными и образуют главную диагональ матрицы.
Для квадратной матрицы главную диагональ образуют элементы 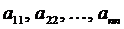 .
.
o Если все недиагональные элементы квадратной матрицы равны нулю, то матрицы называется диагональной.
Пример:
 - диагональная матрица 4-го порядка
- диагональная матрица 4-го порядка
o Если у диагональной матрицы 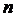 -го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей
-го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей 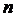 -го порядка и обозначается
-го порядка и обозначается 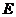 .
.
Пример:
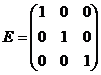 - единичная матрица третьего порядка.
- единичная матрица третьего порядка.
7.Матрица любого размера называется нулевой, или нуль-матрицей, если все ее элементы равны нулю.



III. Операции над матрицами
1). Транспонирование матрицы -
- переход от матрицы 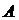 к матрице
к матрице 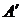 , в которой строки и столбцы поменялись местами. Матрица
, в которой строки и столбцы поменялись местами. Матрица 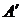 называется транспонированной по отношению к матрице
называется транспонированной по отношению к матрице 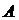 .
.
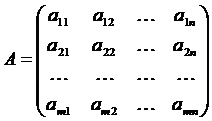 ,
, 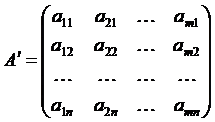 .
.
Пример:
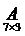 =
=  ;
; 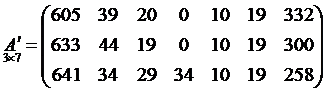
2). Умножение матрицы на число.
Произведением матрицы  на число
на число 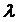 называется матрица
называется матрица 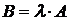 , каждый элемент которой
, каждый элемент которой 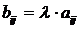 для
для 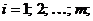
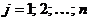 .
.
Т.е., чтобы умножить матрицу на число, надо умножить на это число каждый элемент матрицы.
Пример:
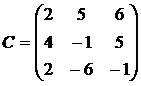 , тогда
, тогда
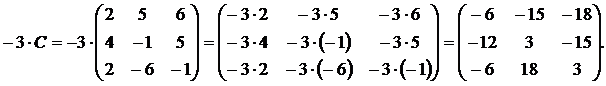
Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
Пример: Вынести за знак матрицы общий множитель.
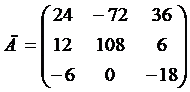 =
= 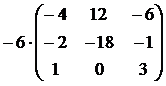 .
.
Произведение матрицы 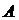 на число
на число 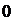 есть нулевая матрица:
есть нулевая матрица: 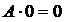 .
.
3) Сложение матриц.
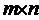 Суммой двух матрицА и В одинакового размера называетсяматрицаС=А+В, каждыйэлементкоторой
Суммой двух матрицА и В одинакового размера называетсяматрицаС=А+В, каждыйэлементкоторой 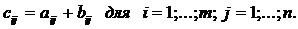
Т.е., чтобы сложить две матрицы одинакового размера, надо сложить их соответствующие элементы.
Пример: 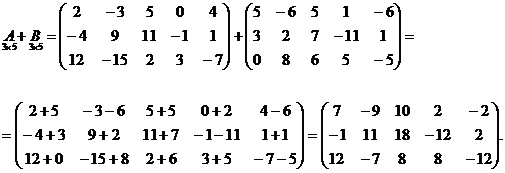
4) Умножение матриц.
Умножение матрицы  на матрицу
на матрицу 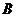 определено, когда число столбцов матрицы
определено, когда число столбцов матрицы  равно число строк матриц
равно число строк матриц 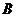 , т.е. они согласованы.
, т.е. они согласованы.
Произведением матриц 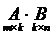 называется такая матрица
называется такая матрица 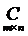 , каждый элемент которой
, каждый элемент которой 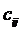 равен сумме произведений элементов строки
равен сумме произведений элементов строки 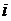 матрицы
матрицы 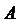 на соответствующие элементы столбца
на соответствующие элементы столбца 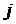 матрицы
матрицы 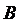 .
.
Пример:
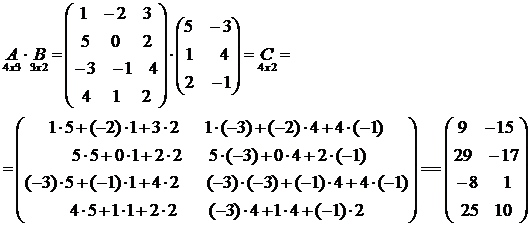
5) Возведение в степень.
Целой положительной степенью 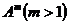 квадратной матрицы
квадратной матрицы  называется произведение
называется произведение 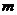 матриц, равных
матриц, равных  , т.е.
, т.е.
 . По определению полагают,
. По определению полагают, 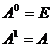 .
.
Пример:
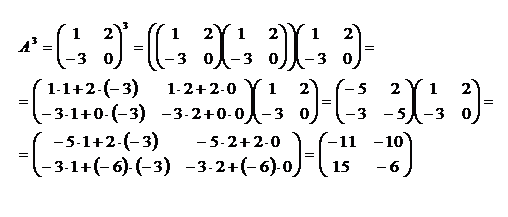
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1) Даны матрицы
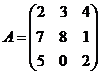 ;
;  ;
; 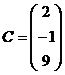 ;
; 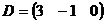 ;
; 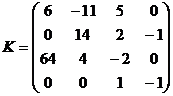
Назвать их элементы, строки, столбцы, размерность, для матриц A и B – элементы главной диагонали.
2) Выполнить сложение матриц A и B:
а) 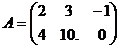 ,
, 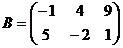 ; б)
; б) 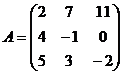 ,
, 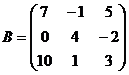 ;
;
в) 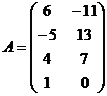 ,
, 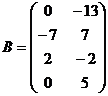 .
.
3) Выполнить умножение A и B:
а) 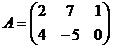 ,
, 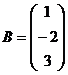 ; б)
; б) 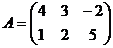 ,
, 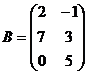 ;
;
в) 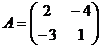 ,
, 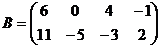 .
.
4) Найти транспонированную матрицу для матрицы:
а) 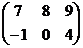 ; б)
; б) 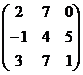 ; в)
; в) 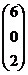 ; г)
; г) 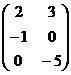 .
.
5) Записать системы линейных алгебраических уравнений в матричной форме:
а). 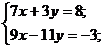 б).
б). 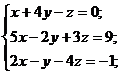 в).
в). 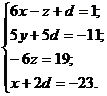
И ИХ СВОЙСТВА»
Свойства определителей.
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1) Правило нахождения определителей второго порядка можно записать в виде формулы:
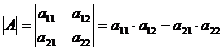
Вычислить определители 2-го порядка матриц:
а) 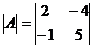 ; б)
; б) 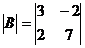 ; в)
; в) 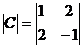 ; г)
; г) 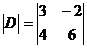 .
.
2) Для вычисления определителей третьего порядка используют правило Сарруса или правило треугольников, которое проще запоминается в виде следующих схем:

 (+) (главная диагональ) (+) (главная диагональ) | 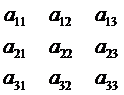 |  (-) (другая диагональ) (-) (другая диагональ) |
Вычислить определители 3-го порядка матриц по правилу Сарруса:
а) 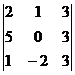 ; б)
; б) 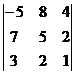 ; в)
; в) 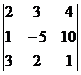 ;
;
3) Для вычисления определителей 4-го и более высокого порядка используют правило вычисления определителя методом разложения по элементам строки или столбца (по теореме Лапласа): определитель равен сумме произведений всех элементов какого-либо столбца (или строки) на соответствующие им алгебраические дополнения. Обычно вычисление проводится по элементам 1-й строки.
Можно использовать теорему Лапласа и для вычисления определителей 3-го порядка, когда разложение по первой строке имеет вид:
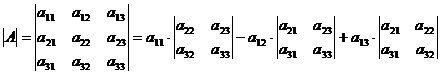
Вычислить определители 4-го и 3-го порядков:
а) 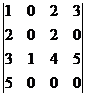 ; б)
; б) 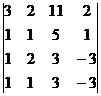 ; в)
; в) 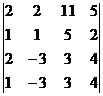 ;
;
г) 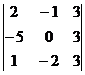 ; д)
; д) 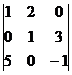 ; е)
; е) 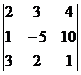 .
.
Замечание: Для сокращения вычислений удобно определитель раскладывать по элементам той строки или столбца, где содержится наибольшее количество нулей.
В этом случае нужно находить алгебраическое дополнения к элементам, равным 0; если же строки или столбцы не содержат достаточного количества нулей, то удобно провести эквивалентные преобразования. Используют правило: если ко всем элементам строки (столбца) прибавить соответствующие элементы другой строки (столбца); умноженные на одно и то же число; то определитель не изменяется.
III. «РАНГ МАТРИЦЫ»
Для решения и исследования некоторых математических и прикладных задач большое значение имеет понятие ранга матрицы.
Рассмотрим матрицу А размера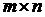 .
.
В матрице А размера 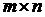 вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы k-го порядка, где
вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы k-го порядка, где 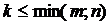 (меньшего из т и п). Определители таких подматриц называются минорами k-го порядка матрицы А. Один элемент матрицы называют минором первого порядка.
(меньшего из т и п). Определители таких подматриц называются минорами k-го порядка матрицы А. Один элемент матрицы называют минором первого порядка.
Из матрицы А размером 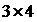 можно получить подматрицы 1-го, 2-го, 3-го порядков.
можно получить подматрицы 1-го, 2-го, 3-го порядков.
Пример: Выделим указанные подматрицы из данной матрицы 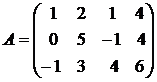 и запишем их миноры.
и запишем их миноры.
Решение:
Некоторые подматрицы первого порядка А 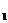 =
= 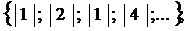
некоторые подматрицы второго порядка А 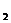 =
= 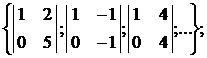
некоторые подматрицы третьего порядка А 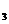 =
= 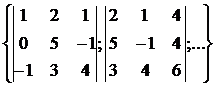 .
.
ОПРЕДЕЛЕНИЕ.Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы.
Обозначение: rang A или r(A)
Из определения следует:
1) 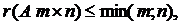 т.е., не превосходит меньшего из ее размеров;
т.е., не превосходит меньшего из ее размеров;
2) 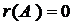 тогда и только тогда, когда все элементы матрицы равны нулю;
тогда и только тогда, когда все элементы матрицы равны нулю;
3) для квадратной матрицы п-го порядка 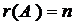 тогда и только тогда, когда матрица А – невырожденная, т.е., ее определитель не равен нулю.
тогда и только тогда, когда матрица А – невырожденная, т.е., ее определитель не равен нулю.
Пример: Вычислить 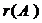 , если
, если
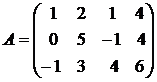 .
.
Решение: Начнем с перебора миноров третьего порядка.
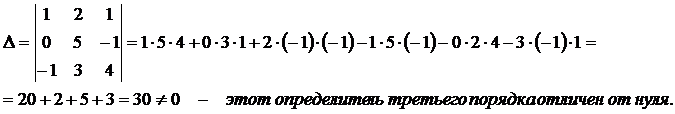 Таким образом, согласно определения ранга матрицы, можем сделать вывод, что ранг данной матрицы равен 3, т.е.,
Таким образом, согласно определения ранга матрицы, можем сделать вывод, что ранг данной матрицы равен 3, т.е., 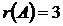 .
.
Замечание: В данном случае вычисление уже первого минора третьего порядка привело к искомому результату. В общем же случае определение ранга матрицы перебором миноров всех возможных порядков достаточно трудоемко.
Для упрощения решения этой задачи используются элементарные преобразования, сохраняющие ранг матрицы:
1)отбрасывание нулевой строки (столбца) матрицы;
2)умножение всех элементов строки (столбца) матрицы на число, не равное нулю;
3)изменение порядка строк (столбцов) матрицы;
4)прибавление к каждому элементу одной строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на одно и то же число;
5)транспонирование матрицы.
ТЕОРЕМА 1:Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Проверить, что ранги указанных матриц равны 2, 3, 2, 1
соответственно: 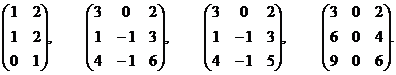
2. С помощью элементарных преобразований вычислить ранг указанных матриц:
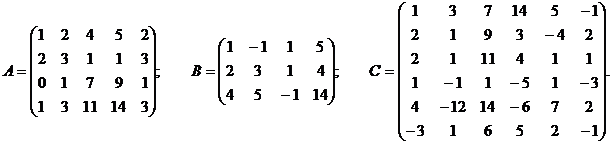
IV. «ОБРАТНАЯ МАТРИЦА».
Определение: Матрица 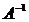 называется обратной по отношению к квадратной матрице
называется обратной по отношению к квадратной матрице 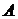 , если при умножении матрицы
, если при умножении матрицы 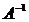 на матрицу
на матрицу 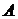 как справа, так и слева, получается единичная матрица:
как справа, так и слева, получается единичная матрица: 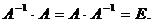
Замечание: Только квадратная матрица имеет обратную. Матрица, обратная данной, тоже квадратная.
Определения: 1. Если определитель матрицы 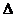 ≠ 0, то матрица называется невырожденной или неособенной.
≠ 0, то матрица называется невырожденной или неособенной.
Если определитель матрицы 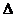 =0, то матрица называется вырожденной или особенной.
=0, то матрица называется вырожденной или особенной.
2. Присоединенная матрица 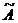 , получается из матрицы
, получается из матрицы 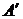 , транспонированной по отношению к матрице
, транспонированной по отношению к матрице 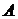 , заменой элементов матрицы
, заменой элементов матрицы 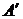 на их алгебраические дополнения.
на их алгебраические дополнения.
Теорема (необходимое и достаточное условие существования обратной матрицы):
Обратная матрица 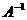 существует и единственна тогда и только тогда, когда матрица
существует и единственна тогда и только тогда, когда матрица  невырожденная, т.е.
невырожденная, т.е. 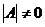 . Ее элементы вычисляются по формуле:
. Ее элементы вычисляются по формуле: 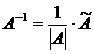 .
.
Алгоритм построения обратной матрицы 1. Вычислим определитель данной матрицы 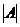 . Если . Если 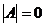 , то для данной матрицы не существует обратной. 2. Если , то для данной матрицы не существует обратной. 2. Если 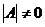 , строим матрицу , строим матрицу 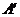 , транспонированную по отношению к матрице , транспонированную по отношению к матрице  , заменяя строки матрицы А ее столбцами. 3. Строим присоединенную матрицу , заменяя строки матрицы А ее столбцами. 3. Строим присоединенную матрицу 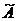 , заменяя элементы матрицы , заменяя элементы матрицы 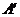 их алгебраическими дополнениями по формуле их алгебраическими дополнениями по формуле 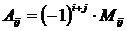 4. Вычисляем обратную матрицу по формуле 4. Вычисляем обратную матрицу по формуле 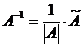 5. При необходимости проверяем правильность вычисления обратной матрицы 5. При необходимости проверяем правильность вычисления обратной матрицы 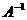 , исходя из ее определения , исходя из ее определения 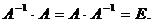 . . |
Пример: 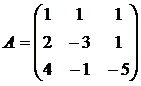 . Найти . Найти 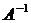 . . |
1. 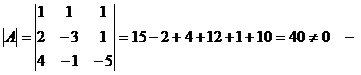 данная матрица имеет обратную. данная матрица имеет обратную. |
2. 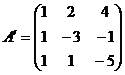 . . |
3. 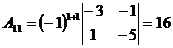 ; ; 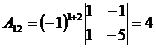 ; ; 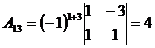 ; ; 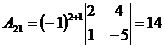 ; ; 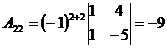 ; ; 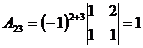 ; ; 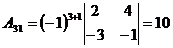 ; ; 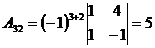 ; ; 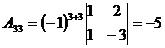 . Получили присоединенную матрицу: . Получили присоединенную матрицу: 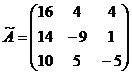 . . |
4. 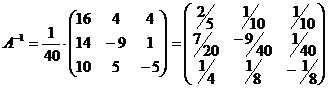 . . |
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Найти матрицу, обратную данной:
1) 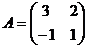 ; 3)
; 3) 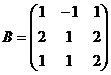 ; 5)
; 5) 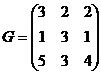 ;
;
2) 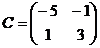 ; 4)
; 4) 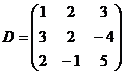 ; 6)
; 6) 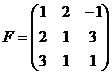 .
.
Проверить для матриц B и D правильность нахождения обратной матрицы (должны быть верными равенства: 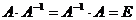 ).
).
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ»
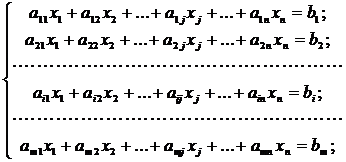
-
- система m линейных уравнений с n переменными, где произвольные числа 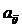
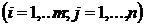 - коэффициенты при переменных,
- коэффициенты при переменных, 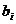
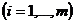 - свободные члены уравнений.
- свободные члены уравнений.
Решением такой системы называется совокупность значений переменных х1, …, хn, при подстановке которых каждое уравнение системы обращается в верное равенство.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Две системы называются равносильными, если они имею одно и тоже множество решений.
Получают их с помощью элементарных преобразований:
1. изменение порядка уравнений в системе;
2. умножение или деление обеих частей любого уравнения системы на одно и то же неравное нулю число;
3. почленное сложение уравнений системы.
Рассматриваемую систему уравнений можно записать в матричной форме:
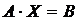 , где
, где
А – матрица коэффициентов при переменных, или матрица системы;
Х – матрица–столбец переменных;
В – матрица–столбец свободных членов, т.е.
 ;
; 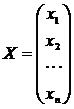 ;
; 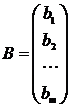 .
.
Мы будем рассматривать системы, где m=n, т.е. количество уравнений в системе и количество входящих в них переменных равны. Тогда матрица А системы квадратная и имеет определитель 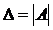 , который называют определителем системы.
, который называют определителем системы.
Такие системы можно решить одним из трех следующих методов:
1. метод Крамера;
2. матричный метод;
3. метод Гаусса.
ПРИМЕР РЕШЕНИЯ СИСТЕМЫ ВСЕМИ ТРЕМЯ МЕТОДАМИ
Решить систему линейных алгебраических уравнений методами Крамера, Гаусса и матричным методом.
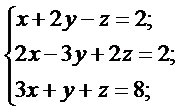
I. Метод Крамера.
Количество уравнений (3) равно количеству переменных (3), значит, матрица системы квадратная и имеет определитель.
Вычислим определитель матрицы системы:
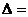
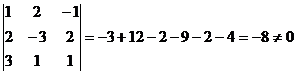 - значит, система уравнений имеет единственное решение, которое находят по формулам Крамера:
- значит, система уравнений имеет единственное решение, которое находят по формулам Крамера: 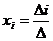 ,
, 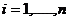 .
.
Заменяем 1–й столбец столбцом свободных членов
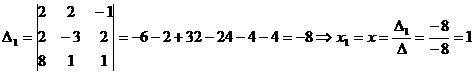
Заменяем 2-й столбец столбцом свободных членов
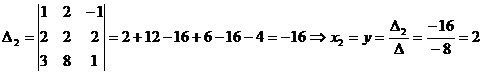
Заменяем 3-й столбец столбцом свободных членов
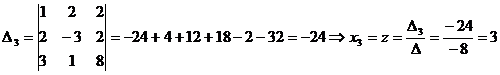
Ответ: 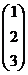 .
.
II. Матричный метод.
Данную систему уравнений можно записать в матричной форме 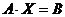 :
:
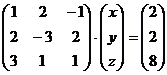 , откуда
, откуда 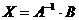 .
.
Найдем матрицу, обратную матрицу  . Так как
. Так как 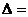
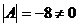 , такая матрица существует. Найдем алгебраические дополнения к элементам матрицы
, такая матрица существует. Найдем алгебраические дополнения к элементам матрицы  по формуле
по формуле 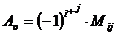 :
:
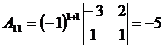 ;
; 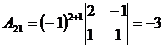 ;
; 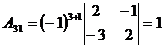 ;
;
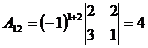 ;
; 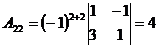 ;
; 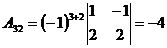 ;
;
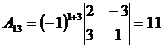 ;
; 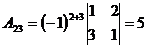 ;
; 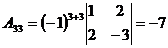 .
.
Тогда
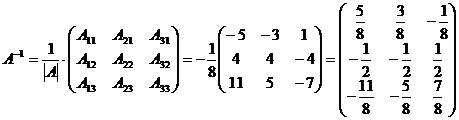 .
.
А теперь найдем решение системы:
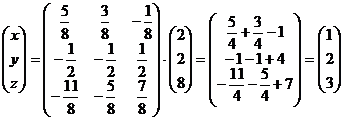 .
.
Ответ: 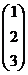 .
.
III. Метод Гаусса.
Выполним преобразования:
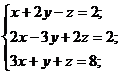
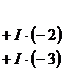 Сделаем коэффициенты при х равными нулю.
Сделаем коэффициенты при х равными нулю.
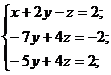
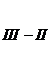 Т.к. коэффициенты при z во II и III уравнениях системы равны, то можно из III уравнения вычесть II уравнение.
Т.к. коэффициенты при z во II и III уравнениях системы равны, то можно из III уравнения вычесть II уравнение.
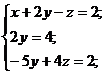 Таким образом, получили, что II уравнение системы есть уравнение с одной переменной, значит, можно вычислить значение переменной у.
Таким образом, получили, что II уравнение системы есть уравнение с одной переменной, значит, можно вычислить значение переменной у.
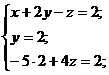 Теперь последовательно, с помощью подстановки, вычисляем значения
Теперь последовательно, с помощью подстановки, вычисляем значения
переменных z и х.
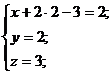
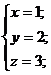
Ответ: 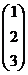 .
.
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
v Необходимые условия применения метода Крамера:
a. Количество уравнений системы должно равняться количеству неизвестных.
b. Определитель основной матрицы системы не должен равняться нулю: 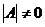 .
.
Решение по правилу Крамера находят по формулам:
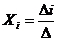 , где
, где 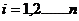 , где
, где 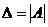 ,
,
а 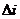 - определитель, который получается из основного определителя матрицы
- определитель, который получается из основного определителя матрицы  заменой
заменой 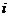 - го столбца столбцом свободных членов системы.
- го столбца столбцом свободных членов системы.
v При решении системы матричным способом сначала надо найти 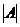 . Система имеет решение при условии
. Система имеет решение при условии 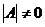 . Затем ищут обратную матрицу к матрицу
. Затем ищут обратную матрицу к матрицу  :
: 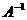 . После этого умножают
. После этого умножают 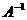 на матрицу – столбец свободных членов системы:
на матрицу – столбец свободных членов системы: 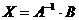
Полученная при этом матрица-столбец и является решением системы.
v Метод Гаусса состоит в приведении системы к треугольному виду. Для системы, состоящей из 3-х уравнений с 3-мя неизвестными метод Гаусса выглядит так: исключаем 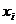 из 2-го и 3-го уравнений системы: затем исключаем
из 2-го и 3-го уравнений системы: затем исключаем 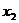 из 3-го уравнения и решаем полученную систему.
из 3-го уравнения и решаем полученную систему.
Решить каждую систему линейных алгебраических уравнений всеми тремя
способами:
1) 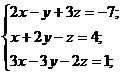 2)
2) 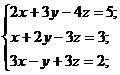 3)
3) 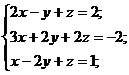
4) 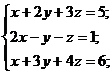 5)
5) 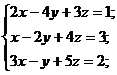 6)
6) 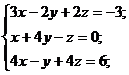
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Операции над матрицами.
1.1. Что такое матрица?
1.2. Какие виды матриц Вы знаете?
1.3. Что означает размер матрицы m?n?
1.4. Какую матрицу называют квадратной?
1.5. Какие две матрицы можно сложить?
1.6. Когда две матрицы можно перемножить?
1.7. Матрицу какого вида можно возвести в степень?
1.8. В чем суть транспонирования матрицы?
1.9. При транспонировании размер матрицы не изменился. Матрицу какого вида транспонировали?
2. Свойства определителей.
2.1. Что можно сказать об определителе матрицы, у которой:
2.1.1 одна строка содержит только нулевые элементы;
2.1.2 элементы двух столбцов равны;
2.1.3 элементы двух строк пропорциональны;
2.1.4 две строки матрицы поменяли местами;
2.1.5 к элементам одного столба прибавили соответствующие элементы другого столбца, умноженные на одно и то же число.
2.2. Сравните определители матрицы  и матрицы
и матрицы 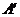 , транспонированной по отношению к матрице
, транспонированной по отношению к матрице  .
.
2.3. Как вычисляют определители квадратных матриц:
2.3.1 второго порядка;
2.3.2 третьего порядка;
2.3.3 четвертого порядка
2.4. Чем матрица отличается от определителя матрицы?
3. Ранг матрицы.
3.1. Что такое ранг матрицы?
3.2. Как проще вычислить ранг матрицы? Какие элементарные преобразования матриц при этом применяются?
4. Обратная матрица.
4.1. Какую матрицу называют обратной?
4.2. Для какой матрицы существует обратная?
4.3. Какой вид имеет обратная матрица?
4.4. Сформулируйте теорему об обратной матрице.
4.5. Перечислите этапы нахождения элементов обратной матрицы.
5. Метод Крамера.
5.1. Сформулируйте теорему Крамера и запишите формулы Крамера.
5.2. Перечислите этапы решения системы неоднородных линейных уравнений методом Крамера.
5.3. Для каких систем уравнений (количество уравнений и переменных в них) применим метод Крамера?
6. Метод Гаусса.
6.1. В чем суть метода Гаусса?
6.2. Что применяют для получения треугольной (ступенчатой) системы уравнений?
6.3. Для каких систем уравнений (количество уравнений и переменных в них) применим метод Гаусса?
7. Матричный метод.
7.1. В чем суть матричного метода?
7.2. Для каких систем уравнений (количество уравнений и переменных в них) применим матричный метод?
7.3. Матрицу какого вида используют для решения системы матричным методом?
7.4. Какое равенство используют для решения системы матричным методом?
ЗАДАНИЯ ДЛЯ САМОПРОВЕРКИ
Вариант I
1. Данная запись есть
а) Матрица размера mxn;
б) Определитель 3го порядка;
в) Матрица 4го порядка.
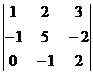
2. Если элементы двух строк матрицы пропорциональны, то ее определитель равен:
а) 1;
б) 0;
в) -1
3. Данная матрица есть
а) Ди
