Основные сведения о матрицах
Ответы к экзамену по математике
Линейная алгебра.
Основные сведения о матрицах
В этом разделе мы даем основные сведения о матрицах, необходимые для понимания статистики и анализа данных.
Матрицей размера mxn (читается m на n)называется прямоугольная таблица чисел, содержащая m строк и n столбцов.
Числа, составляющие матрицу, называются элементами матрицы.
Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, A, B, C,….
Для обозначения элементов матрицы используются строчные буквы с двойным индексом, например: aij, где i - номер строки, j - номер столбца.
Например, матрица:
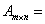
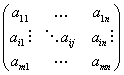
В сокращенной записи обозначаем A=(aij); i=1,2,…m; j=1,2,…,n
Приведем пример матрицы 2 на 2: 
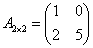

Вы видите, что a11 = 1, a12 = 0, a21 = 2, a22=5
Наряду с круглыми скобками используются и другие обозначения матрицы: 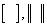
Две матрицы A и B одного размера называются равными, если они совпадают поэлементно, aij = bij для любых i=1,2,…m; j=1,2,…n
Виды матриц. Матрица, состоящая из одной строки, называется матрицей (вектором)- строкой, а из одного столбца - матрицей (вектором)- столбцом:
A=(a11,a12,…,a1n) - матрица - строка
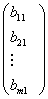
B= 
Матрица называется квадратной n-го порядка, если число ее строк равно числу столбцов и равно n.
Например, 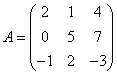 порядака.
порядака.
Элементы матрицы aij, у которых номер столбца равен номеру строки называются диагональными и образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы a11, a22,…,ann.
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.
А)Операции над матрицами
Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциями над числами, а некоторые - специфические.
1. Умножение матрицы на число. Произведение матрицы А на число 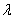 называется матрица B=
называется матрица B= 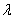 A, элементы которой bij=
A, элементы которой bij= 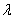 aij для i=1,2,…m; j=1,2,…n
aij для i=1,2,…m; j=1,2,…n
Следствие: Общий множитель всех элементов матрицы можно выносить за знак матрицы.
В частности, произведение матрицы А на число 0 есть нулевая матрица.
2. Сложение матриц. Суммой двух матриц А и В одинакового размера m 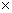 называется матрица С=А+В, элементы которой cij=aij+bij для i=1,2,…m; j=1,2,…n (т.е. матрицы складываются поэлементно).
называется матрица С=А+В, элементы которой cij=aij+bij для i=1,2,…m; j=1,2,…n (т.е. матрицы складываются поэлементно).
3. Вычитание матриц. Разность двух матриц одинакового размера определяется через предыдущие операции: A-B=A+(-1)∙B.
4. Умножение матриц. Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц Am 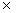 ∙B k
∙B k 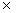 называется такая матрица Cm
называется такая матрица Cm 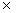 , каждый элемент которой cij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В:
, каждый элемент которой cij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В:
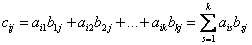 i=1,2,…,m; j=1,2,…,n
i=1,2,…,m; j=1,2,…,n
Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (что следует из этих операций):
A+B=B+A
(A+B)+C=A+(B+C)
λ (A+B)= λA+ λB
A(B+C)=AB+AC
(A+B)C=AC+BC
λ (AB)=( λA)B=A(λB)
A(BC)=(AB)C
Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые от умножения чисел:
a) АВ существует, то после перестановки сомножителей местами произведение матриц ВА может и не существовать.
b) АВ и ВА существуют, то они могут быть матрицами разных размеров.
5. Транспонирование матрицы - переход от матрицы А к матрице А', в которой строки и столбцы поменялись местами с сохранением порядка. Матрица А' называется транспонированной относительно матрицы А:
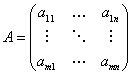
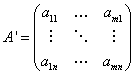
Из определения следует, что если матрица А имеет размер m 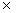 , то транспонированная матрица А' имеет размер n
, то транспонированная матрица А' имеет размер n 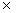
В литературе встречаются и другие обозначения транспонированной матрицы, например, АТ
Рассмотрим квадратную матрицу
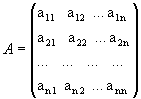 .
.
Обозначим D =det A.
Б)ОБРАТНАЯ МАТРИЦА
Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если D = 0.
Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.
Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
Матрица, обратная матрице А, обозначается через А-1, так что В = А-1. Обратная матрица вычисляется по формуле
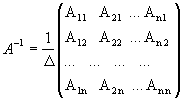 , (4.5)
, (4.5)
где А i j - алгебраические дополнения элементов a i j.
Вычисление обратной матрицы по формуле (4.5) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.
Пример 2.10. Для матрицы 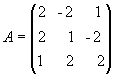 найти обратную.
найти обратную.
Решение. Находим сначала детерминант матрицы А
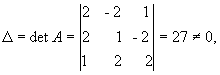 значит, обратная матрица существует и мы ее можем найти по формуле:
значит, обратная матрица существует и мы ее можем найти по формуле: 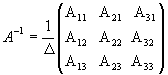 , где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j исходной матрицы.
, где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j исходной матрицы. 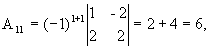
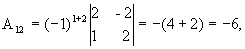
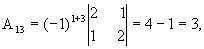
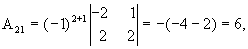
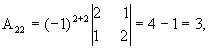
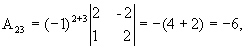
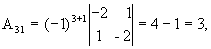
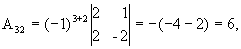
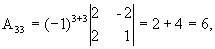
откуда 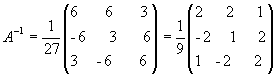 .
.
Пример 2.11. Методом элементарных преобразований найти обратную матрицу для матрицы: А= 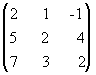 .
.
Решение. Приписываем к исходной матрице справа единичную матрицу того же порядка: 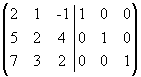 . С помощью элементарных
. С помощью элементарных
преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие преобразования над правой матрицей.
Для этого поменяем местами первый и второй столбцы: 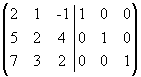 ~
~ 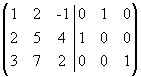 . К третьему столбцу прибавим первый, а ко второму - первый, умноженный на -2:
. К третьему столбцу прибавим первый, а ко второму - первый, умноженный на -2: 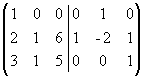 . Из первого столбца вычтем удвоенный второй, а из третьего - умноженный на 6 второй;
. Из первого столбца вычтем удвоенный второй, а из третьего - умноженный на 6 второй; 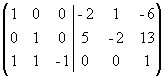 . Прибавим третий столбец к первому и второму:
. Прибавим третий столбец к первому и второму: 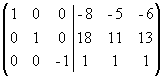 . Умножим последний столбец на -1:
. Умножим последний столбец на -1: 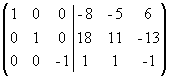 . Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице А. Итак,
. Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице А. Итак,
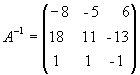 .
.
В) Ранг матрицы
Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.
Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.
Ранг матрицы — Размерность образа dim(im(A)) линейного оператора, которому соответствует матрица.
Обычно ранг матрицы A обозначается 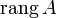 (
( 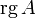 ) или
) или 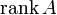 . Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — для немецкого, французского и ряда других языков.
. Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — для немецкого, французского и ряда других языков.
Определение
Пусть 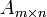 — прямоугольная матрица.
— прямоугольная матрица.
Тогда по определению рангом матрицы A является:
- ноль, если A — нулевая матрица;
- число
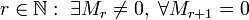 , где Mr — минор матрицы A порядка r, а Mr + 1 — окаймляющий к нему минор порядка (r + 1), если они существуют.
, где Mr — минор матрицы A порядка r, а Mr + 1 — окаймляющий к нему минор порядка (r + 1), если они существуют.
Теорема (о корректности определения рангов). Пусть все миноры матрицы 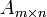 порядка k равны нулю (Mk = 0). Тогда порядка k равны нулю (Mk = 0). Тогда 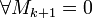 , если они существуют. , если они существуют. |
Связанные определения
- Ранг
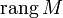 матрицы M размера
матрицы M размера 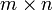 называют полным, если
называют полным, если 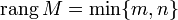 .
. - Базисный минор матрицы A — любой ненулевой минор матрицы A порядка r, где
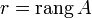 .
. - Строки и столбцы, на пересечении которых стоит базисный минор, называются базисными строками и столбцами. (Они определены неоднозначно в силу неоднозначности базисного минора.)
Свойства
- Теорема (о базисном миноре): Пусть
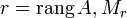 — базисный минор матрицы A, тогда:
— базисный минор матрицы A, тогда: - базисные строки и базисные столбцы линейно независимы;
- любая строка (столбец) матрицы A есть линейная комбинация базисных строк (столбцов).
- Следствия:
- Если ранг матрицы равен r, то любые p:p > r строк или столбцов этой матрицы будут линейно зависимы.
- Если A — квадратная матрица, и
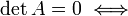 , то строки и столбцы этой матрицы линейно зависимы.
, то строки и столбцы этой матрицы линейно зависимы. - Пусть
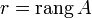 , тогда максимальное количество линейно независимых строк (столбцов) этой матрицы равно r.
, тогда максимальное количество линейно независимых строк (столбцов) этой матрицы равно r. - Теорема (об инвариантности ранга при элементарных преобразованиях): Введём обозначение A∼B для матриц, полученных друг из друга элементарными преобразованиями. Тогда справедливо утверждение: Если A∼B, то их ранги равны.
- Теорема Кронекера — Капелли: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. В частности:
- Количество главных переменных системы равно рангу системы.
- Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.
Линейное преобразование и ранг матрицы
Пусть A — матрица размера 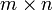 над полем C (или R). Пусть T — линейное преобразование, соответствующее A в стандартном базисе; это значит, что T(x) = Ax. Ранг матрицы A — это размерность области значений преобразования T.
над полем C (или R). Пусть T — линейное преобразование, соответствующее A в стандартном базисе; это значит, что T(x) = Ax. Ранг матрицы A — это размерность области значений преобразования T.
Методы
Существует несколько методов нахождения ранга матрицы:
- Метод элементарных преобразований
Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.
- Метод окаймляющих миноров
Пусть в матрице A найден ненулевой минор k-го порядка M. Рассмотрим все миноры (k + 1)-го порядка, включающие в себя (окаймляющие) минор M; если все они равны нулю, то ранг матрицы равен k. В противном случае среди окаймляющих миноров найдется ненулевой, и вся процедура повторяется.
2. ОПРЕДЕЛИТЕЛИ КВАДРАТНЫХ МАТРИЦ
Решение.
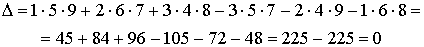
Замечание. Вычисление определителей четвертого и более высокого порядка приводит к большим вычислениям, так как
· для нахождения определителя первого порядка мы находим одно слагаемое, состоящее из одного сомножителя,
· для нахождения определителя второго порядка нужно вычислить алгебраическую сумму из двух слагаемых, где каждое слагаемое состоит из произведения двух сомножителей,
· для нахождения определителя третьего порядка нужно вычислить алгебраическую сумму из шести слагаемых, где каждое слагаемое состоит из произведения трех сомножителей,
· для нахождения определителя четвертого порядка нужно вычислить алгебраическую сумму из двадцати четырех слагаемых, где каждое слагаемое состоит из произведения четырех сомножителей и т.д.
Определить количество слагаемых в алгебраической сумме, можно вычислив факториал:
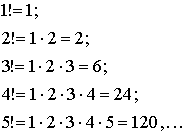
Вычисление определителя четвертого порядка приводит к большим вычислениям. Поэтому в этом случае используют искусственные методы, о которых мы остановимся позже.
А)Основные свойства определителей.
Свойство 1. Определитель квадратной матрицы не изменяется при её транспонировании:
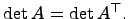
Доказательство свойства 1 для квадратных матриц 2 и 3 порядков проводится по единой схеме. Приведём доказательство для квадратной матрицы 2-го порядка. Непосредственная проверка доказывает данное свойство.
Свойство 2. Если одна из строк (столбцов) матрицы целиком состоит из нулей, то её <#146#>определитель] равен нулю.
Свойство 2 непосредственно вытекает из определения определителя.
Свойство 3. При перестановке местами любых двух строк (столбцов) матрицы её определитель меняет знак.
Свойство 4. При умножении строки (столбца) матрицы на число её определитель умножается на это число.
Свойство 5. Если каждый элемент i-й строки (столбца) матрицы A представлен в виде суммы двух слагаемых, то определитель такой матрицы равен 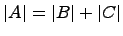 , где элементы матриц B и C, за исключением элементов i-й строки (столбца), совпадают с соответствующими элементами матрицы A. A в i-х строках (столбцах) матриц B и C стоят упомянутые первые и вторые слагаемые соответственно.
, где элементы матриц B и C, за исключением элементов i-й строки (столбца), совпадают с соответствующими элементами матрицы A. A в i-х строках (столбцах) матриц B и C стоят упомянутые первые и вторые слагаемые соответственно.
Отметим некоторые следствия, непосредственно вытекающие из перечисленных 5 основных свойств определителя.
Следствие 1. Определитель матрицы, имеющей две одинаковые строки (столбца) равен нулю.
Доказательство. Пусть A - квадратная матрица, имеющая две одинаковые строки (столбца). B - матрица полученная в результате перестановки указанных одинаковых строк (столбцов) матрицы A. Тогда, с одной стороны, 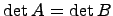 , с другой стороны, в силу свойства 3,
, с другой стороны, в силу свойства 3, 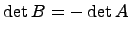 . Следовательно,
. Следовательно, 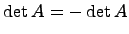 . Из последнего равенства следует, что
. Из последнего равенства следует, что 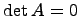 .
.
Следствие 2. Если какие-либо две строки (столбца) матрицы пропорциональны, то её определитель равен нулю.
Следствие 3. Если к элементам какой-либо строки (столбца) прибавить соответствующие элементы любой другой строки (столбца), умноженные на любое число 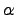 , то определитель не изменится.
, то определитель не изменится.
3. А)Системы линейных уравнений: основные понятия
Определение. Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:

Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.
Определение. Решение системы уравнений — это последовательность чисел (k1, k2, ..., kn), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x1, x2, ..., xn дает верное числовое равенство.
Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:
- Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.
- Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.
- Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество.
Определение. Переменная xi называется разрешенной, если она входит только в одно уравнение системы, причем с коэффициентом 1. Другими словами, в остальных уравнениях коэффициент при переменной xi должен быть равен нулю.
Если в каждом уравнении выбрать по одной разрешенной переменной, получим набор разрешенных переменных для всей системы уравнений. Сама система, записанная в таком виде, тоже будет называться разрешенной. Вообще говоря, одну и ту же исходную систему можно свести к разным разрешенным, однако сейчас нас это не волнует. Вот примеры разрешенных систем:
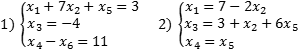
Обе системы являются разрешенными относительно переменных x1, x3 и x4. Впрочем, с тем же успехом можно утверждать, что вторая система — разрешенная относительно x1, x3 и x5. Достаточно переписать самое последнее уравнение в виде x5 = x4.
Теперь рассмотрим более общий случай. Пусть всего у нас k переменных, из которых r являются разрешенными. Тогда возможны два случая:
- Число разрешенных переменных r равно общему числу переменных k: r = k. Получаем систему из k уравнений, в которых r = k разрешенных переменных. Такая система является совместной и определенной, т.к. x1 = b1, x2 = b2, ..., xk = bk;
- Число разрешенных переменных r меньше общего числа переменных k: r < k. Остальные (k − r) переменных называются свободными — они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.
Так, в приведенных выше системах переменные x2, x5, x6 (для первой системы) и x2, x5 (для второй) являются свободными. Случай, когда есть свободные переменные, лучше сформулировать в виде теоремы:
Теорема. Если в системе из n уравнений переменные x1, x2, ..., xr — разрешенные, а xr + 1, xr + 2, ..., xk — свободные, то:
- Если задать значения свободным переменным (xr + 1 = tr + 1, xr + 2 = tr + 2, ..., xk = tk), а затем найти значения x1, x2, ..., xr, получим одно из решений.
- Если в двух решениях значения свободных переменных совпадают, то значения разрешенных переменных тоже совпадают, т.е. решения равны.
В чем смысл этой теоремы? Чтобы получить все решения разрешенной системы уравнений, достаточно выделить свободные переменные. Затем, присваивая свободным переменным разные значения, будем получать готовые решения. Вот и все — таким образом можно получить все решения системы. Других решений не существует.
Вывод: разрешенная система уравнений всегда совместна. Если число уравнений в разрешенной системе равно числу переменных, система будет определенной, если меньше — неопределенной.
И все бы хорошо, но возникает вопрос: как из исходной системы уравнений получить разрешенную? Для этого существует метод Гаусса.
Б) Методы решения систем линейных алгебраических уравнений
Прямые методы решения СЛАУ:
Метод Крамера
Метод обратной матрицы
Метод Гаусса
Итерационные методы решения линейных алгебраических систем:
Метод простой итерации или метод Якоби
Метод Гаусса – Зейделя
К решению систем линейных алгебраических уравнений сводятся многочисленные практические задачи ( по некоторым оценкам более 75% всех задач). Можно с полным основанием утверждать, что решение линейных систем является одной из самых распространенных и важных задач вычислительной математики.
Конечно, существует много методов и современных пакетов прикладных программ для решения СЛАУ, но для того, чтобы их успешно использовать, необходимо разбираться в основах построения методов и алгоритмов, иметь представления о недостатках и преимуществах используемых методов.
Постановка задачи
Требуется найти решение системы m линейных уравнений, которая записывается в общем виде как
 ,
,
Эту систему уравнений можно записать также в матричном виде:
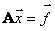 ,
,
где  ,
, 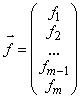 ,
, 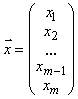 .
.
A – матрица системы, 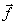 – вектор правых частей,
– вектор правых частей, 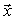 – вектор неизвестных.
– вектор неизвестных.
При известных A и 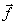 требуется найти такие
требуется найти такие 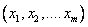 , при подстановке которых в систему уравнений она превращается в тождество.
, при подстановке которых в систему уравнений она превращается в тождество.
Необходимым и достаточным условием существования единственного решения СЛАУ является условие det A≠0, т.е. определитель матрицы A не равен нулю. В случае равенства нулю определителя матрица A называется вырожденной и при этом СЛАУ либо не имеет решения, либо имеет их бесчисленное множество.
В дальнейшем будем предполагать наличие единственного решения.
Все методы решения линейных алгебраических задач можно разбить на два класса: прямые (точные) и итерационные (приближенные).
Прямые методы решения СЛАУ
Метод Крамера
При небольшой размерности системы m (m = 2,…,5) на практике часто используют формулы Крамера для решения СЛАУ:
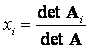 (i = 1, 2, …, m). Эти формулы позволяют находить неизвестные в виде дробей, знаменателем которых является определитель матрицы системы, а числителем – определители матриц Ai, полученных из A заменой столбца коэффициентов при вычисляемом неизвестном столбцом свободных членов. Так А1 получается из матрицы А заменой первого столбца на столбец правых частей f.
(i = 1, 2, …, m). Эти формулы позволяют находить неизвестные в виде дробей, знаменателем которых является определитель матрицы системы, а числителем – определители матриц Ai, полученных из A заменой столбца коэффициентов при вычисляемом неизвестном столбцом свободных членов. Так А1 получается из матрицы А заменой первого столбца на столбец правых частей f.
Например, для системы двух линейных уравнений
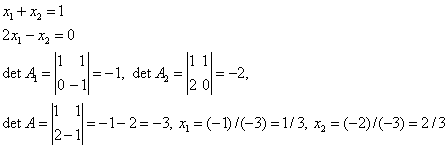
Размерность системы (т.е., число m) является главным фактором, из–за которого формулы Крамера не могут быть использованы для численного решения СЛАУ большого порядка. При непосредственном раскрытии определителей решение системы с m неизвестными требует порядка m!*m арифметических операций. Таким образом, для решения системы, например, из m = 100 уравнений потребуется совершить 10158 вычислительных операций (процесс займёт примерно 1019 лет), что не под силу даже самым мощным современным ЭВМ
Метод обратной матрицы
Если det A ≠ 0, то существует обратная матрица 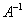 . Тогда решение СЛАУ записывается в виде:
. Тогда решение СЛАУ записывается в виде: 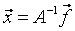 . Следовательно, решение СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы. Проблемы использования этого метода те же, что и при использовании метода Крамера: нахождение обратной матрицы – трудоемкая операция.
. Следовательно, решение СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы. Проблемы использования этого метода те же, что и при использовании метода Крамера: нахождение обратной матрицы – трудоемкая операция.
Метод Гаусса
Наиболее известным и популярным прямым методом решения СЛАУ является метод Гаусса. Этот метод заключается в последовательном исключении неизвестных. Пусть в системе уравнений
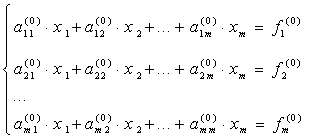
первый элемент 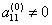 . Назовем его ведущим элементом первой строки. Поделим все элементы этой строки на
. Назовем его ведущим элементом первой строки. Поделим все элементы этой строки на 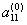 и исключим x1 из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при
и исключим x1 из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при 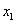 в соответствующей строке. Получим
в соответствующей строке. Получим
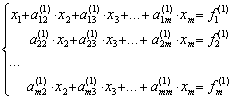 .
.
Если 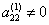 , то, продолжая аналогичное исключение, приходим к системе уравнений с верхней треугольной матрицей
, то, продолжая аналогичное исключение, приходим к системе уравнений с верхней треугольной матрицей
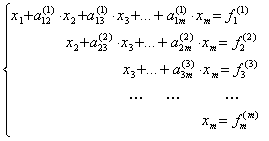 .
.
Из нее в обратном порядке находим все значения xi:
 .
.
Процесс приведения к системе с треугольной матрицей называется прямым ходом, а нахождения неизвестных –обратным. В случае если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Кроме того, если какие–либо ведущие элементы малы, то это приводит к усилению ошибок округления и ухудшению точности счета. Поэтому обычно используется другой вариант метода Гаусса – схема Гаусса с выбором главного элемента. Путем перестановки строк, а также столбцов с соответствующей перенумерацией коэффициентов и неизвестных добиваются выполнения условия:
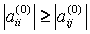 , j = i+1,i+ 2, …, m;
, j = i+1,i+ 2, …, m;
т.е. осуществляется выбор первого главного элемента. Переставляя уравнения так, чтобы в первом уравнении коэффициент a11 был максимальным по модулю. Разделив первую строку на главный элемент, как и прежде, исключают x1 из остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй главный элемент и т.д.
Рассмотрим применение метода Гаусса с выбором главного элемента на примере следующей системы уравнений:
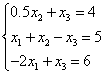
В первом уравнении коэффициент при 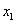 =0, во втором = 1 и в третьем = -2, т.е. максимальный по модулю коэффициент в третьем уравнении. Поэтому переставим третье и первое уравнение:
=0, во втором = 1 и в третьем = -2, т.е. максимальный по модулю коэффициент в третьем уравнении. Поэтому переставим третье и первое уравнение:
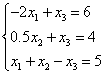
Исключим 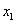 из второго и третьего уравнений с помощью первого. Во втором уравнении исключать не надо. Для исключения из третьего уравнения умножим первое на 0.5 и сложим с третьим:
из второго и третьего уравнений с помощью первого. Во втором уравнении исключать не надо. Для исключения из третьего уравнения умножим первое на 0.5 и сложим с третьим:
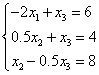
Рассмотрим второе и третье уравнения. Максимальный по модулю элемент при 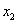 в третьем. Поэтому поместим его на место второго:
в третьем. Поэтому поместим его на место второго:
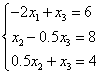
Исключим 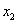 из третьего уравнения. Для этого умножим второе на -0.5 и сложим с третьим:
из третьего уравнения. Для этого умножим второе на -0.5 и сложим с третьим:
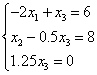
Обратный ход: 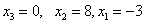 .
.
Проверка: 0.5*8+0=4, -3+8-0=5, -2*(-3)+0=6.
Такая перестановка уравнений необходима для того, чтобы уменьшить влияние ошибок округления на конечный результат.
Часто возникает необходимость в решении СЛАУ, матрицы которые являются слабо заполненными, т.е. содержат много нулевых элементов. В то же время эти матрицы имеют определенную структуру. Среди таких систем выделим системы с матрицами ленточной структуры, в которых ненулевые элементы располагаются на главной диагонали и на нескольких побочных диагоналях. Для решения систем с ленточными матрицами коэффициентов вместо метода Гаусса можно использовать более эффективные методы. Например, метод прогонки, который мы рассмотрим позже при решении краевой задачи для обыкновенного дифференциального уравнения второго порядка.
Метод Гаусса – Зейделя
Расчетные формулы имеют вид:
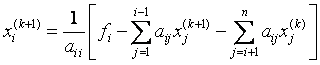
т.е. для подсчета i–й компоненты (k+1)–го приближения к искомому вектору используется уже вычисленное на этом, т.е. (k+1)–м шаге, новые значения первых i–1 компонент.
Подробные формулы имеют вид:

Достаточное условие сходимости этого метода такое же, как и для метода простой итерации, т.е. диагональное преобладание:

Начальное приближение:
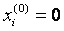
Операции над векторами
Над векторами по определённым правилам можно выполнять линейные операции: складывать их, умножать на число, вычитать. Введём линейные операции над векторами.
Произведением вектора
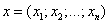
на действительное число 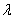 называется вектор
называется вектор
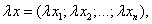
т.е. при умножении вектора на число каждая его координата умножается на это число.
Зная вектор
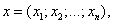
можно получить противоположный вектор
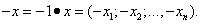
Суммой векторов
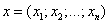
и
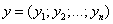
называется вектор
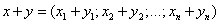 ,
,
т.е. при сложении векторов одной и той же размерности их соответствующие координаты почленно складываются.
Если в плане продаж сети торговых предприятий продажи товаров определить как положительные уровни товаров, а затраты на продажи – как отрицательные, то получим вектор затрат-продаж
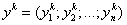 ,
,
где
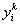 -
-
продажи (затраты) k – м предприятием товара i, а k = 1, 2, 3,…, m .
Суммарный вектор затрат-продаж y определяется суммированием векторов затрат-продаж всех mпредприятий сети:
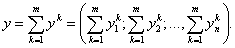
Сумма противоположных векторов даёт нулевой вектор:
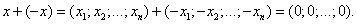
При вычитании двух векторов одной и той же размерности их соответствующие координаты почленно вычитаются:
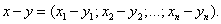
Линейные операции над векторами удовлетворяют следующим свойствам.
Свойство 1.
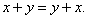
Свойство 2.
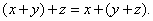
Свойство 3.
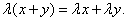
Свойство 4.
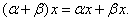
Свойство 5.
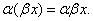
Свойство 6.
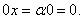
Скалярным произведением двух векторов
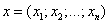
и
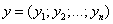
называется число
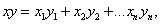
равное сумме произведений соответствующих координат векторов.
В экономических задачах можно рассматривать скалярное произведение вектора цен p
на вектор объёма проданных товаров x . Скалярное произведение px в этом случае даёт суммарную стоимость проданных товаров x при ценах p . Например, если объём всех товаров, проданных предприятием, выражается вектором x = (400; 750; 200; 300), элементы которого означают соответственно количество товаров различных групп, а цены в одних и тех же денежных единицах заданы в соответствующем порядке вектором p = (3; 2,1; 1,2; 0,5), то скалярное произведение
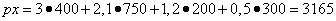
выражает суммарную стоимость всех товаров x .
Скалярное произведение векторов обладает следующими свойствами:
Свойство 1.
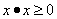 , причём
, причём 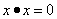 лишь при
лишь при 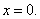
Свойство 2.
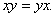
Свойство 3.
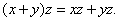
Свойство 4.
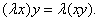
Число
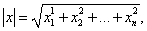
равное квадратному корню из суммы квадратов координат вектора, называется модулем (или длиной) вектора
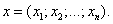
Пример 1.Найти длину вектора x = (3; 0; 4).
Решение. Длина вектора равна
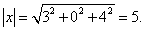
Два вектора называют ортогональными, если их скалярное произведение равно нулю.
Пример 2.Ортогональны ли векторы x = (3; 0; 1; -1) y = (-2; 5; 6; 0)?
Решение. Найдём скалярное произведение
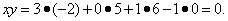
Итак, два данных вектора ортогональны.
Б) Скалярное произведение
Скалярное произведение векторов 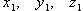 и
и 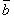 :
: 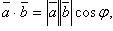
где 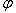 - угол между векторами
- угол между векторами
